LeetCode 2106. 摘水果

2106. 摘水果

在一个无限的 x 坐标轴上，有许多水果分布在其中某些位置。给你一个二维整数数组 fruits ，其中 fruits[i] = [positioni, amounti] 表示共有 amounti 个水果放置在 positioni 上。fruits 已经按 positioni 升序排列 ，每个 positioni 互不相同 。

另给你两个整数 startPos 和 k 。最初，你位于 startPos 。从任何位置，你可以选择 向左或者向右 走。在 x 轴上每移动 一个单位 ，就记作 一步 。你总共可以走 最多 k 步。你每达到一个位置，都会摘掉全部的水果，水果也将从该位置消失（不会再生）。

返回你可以摘到水果的 最大总数 。

示例 1：

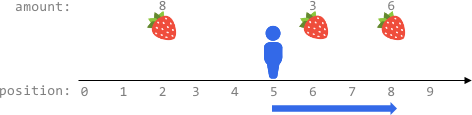
输入：fruits = [[2,8],[6,3],[8,6]], startPos = 5, k = 4
输出：9
解释：
最佳路线为：
- 向右移动到位置 6 ，摘到 3 个水果
- 向右移动到位置 8 ，摘到 6 个水果
移动 3 步，共摘到 3 + 6 = 9 个水果

示例 2：

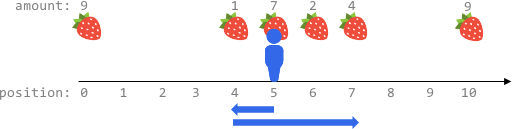
输入：fruits = [[0,9],[4,1],[5,7],[6,2],[7,4],[10,9]], startPos = 5, k = 4
输出：14
解释：
可以移动最多 k = 4 步，所以无法到达位置 0 和位置 10 。
最佳路线为：
- 在初始位置 5 ，摘到 7 个水果
- 向左移动到位置 4 ，摘到 1 个水果
- 向右移动到位置 6 ，摘到 2 个水果
- 向右移动到位置 7 ，摘到 4 个水果
移动 1 + 3 = 4 步，共摘到 7 + 1 + 2 + 4 = 14 个水果

示例 3：

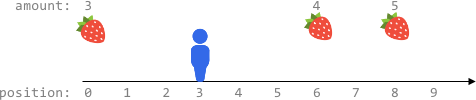
输入：fruits = [[0,3],[6,4],[8,5]], startPos = 3, k = 2
输出：0
解释：
最多可以移动 k = 2 步，无法到达任一有水果的地方

提示：

• 1 <= fruits.length <= 10^5
• fruits[i].length == 2
• 0 <= startPos, positioni <= 2 * 10^5
• 对于任意 i > 0 ，positioni-1 < positioni 均成立（下标从 0 开始计数）
• 1 <= amounti <= 10^4
• 0 <= k <= 2 * 10^5

---

提示 1

Does an optimal path have very few patterns? For example, could a path that goes left, turns and goes right, then turns again and goes left be any better than a path that simply goes left, turns, and goes right?

---

提示 2

The optimal path turns at most once. That is, the optimal path is one of these: to go left only; to go right only; to go left, turn and go right; or to go right, turn and go left.

---

提示 3

Moving x steps left then k-x steps right gives you a range of positions that you can reach.

---

提示 4

Use prefix sums to get the sum of all fruits for each possible range.

---

提示 5

Use a similar strategy for all the paths that go right, then turn and go left.

解法1：二分查找 

假设人先向左走 x 步，然后回到原点，再向右走 y 步，那么区间长度就是：2 * x + y，其中

2 * x + y = k ，y = k - 2 * x，移动区间表示为 [startPos - x, startPos + y] 。

同理，如果先向右走 x 步，然后回到原点，再向左走 y 步，

那么移动区间表示为 [startPos - y, startPos + x] 。

假设已知道当前采摘人员在 x 轴上的移动区间范围，则我们利用二分查找即可在 O(log⁡n)时间复杂度内找到区间中包含的水果的数量，实际可以用前缀和进行预处理即可。

class Solution {
    public int maxTotalFruits(int[][] fruits, int startPos, int k) {
        int n = fruits.length;
        // prefix[i] = fruits[0][1] + ... + fruits[i - 1][1]
        int[] prefix = new int[n + 1];
        // pos[i] = fruits[i][0]
        int[] pos = new int[n];
        for (int i = 1; i <= n; i++) {
            prefix[i] = prefix[i - 1] + fruits[i - 1][1];
            pos[i - 1] = fruits[i - 1][0];
        }
        int ans = 0;
        for (int x = 0; x <= k; x++) {
            int y = k - 2 * x;
            int left = startPos - x;
            int right = startPos + y;
            int start = lowerBound(pos, left);
            int end = upperBound(pos, right);
            ans = Math.max(ans, prefix[end + 1] - prefix[start]);
            left = startPos - y;
            right = startPos + x;
            start = lowerBound(pos, left);
            end = upperBound(pos, right);
            ans = Math.max(ans, prefix[end + 1] - prefix[start]);
            
        }
        return ans;
    }

    // 找到最接近target且可到达的pos[i]，target <= pos[i] = start,返回pos下标i，
    private int lowerBound(int[] pos, int target) {
        // 闭区间写法
        int l = 0;
        int r = pos.length - 1;
        while (l <= r) {
            // 循环不变量：
            // pos[left - 1] < target
            // pos[right + 1] >= target 
            int mid = l + (r - l) / 2;
            if (pos[mid] < target) {
                l = mid + 1;
            } else {
                r = mid - 1;
            }
        }
        // l == r + 1
        return l;
    }
    // 找到最接近target且可到达的pos[i]，end = pos[i] <= target，返回pos下标i，
    private int upperBound(int[] pos, int target) {
        // 闭区间写法
        int l = 0;
        int r = pos.length - 1;
        while (l <= r) {
            // 循环不变量：
            // pos[left - 1] <= target
            // pos[right + 1] > target 
            int mid = l + (r - l) / 2;
            if (pos[mid] > target) {
                r = mid - 1;
            } else {
                l = mid + 1;
            }
        }
        // l == r + 1
        return r;
    }
}

复杂度分析

• 时间复杂度：O(n + k log n)，n 是 数组 fruits 的长度，k 是给定的整数 k。计算数组的前缀和需要的时间为 O(n)，每次查询区间中的水果数量时需要的时间为 O(log ⁡n)，一共最多有 k 次查询，因此总的时间复杂度即为 O(n + k log n)。
• 空间复杂度：O(n)。其中 n 是 数组 fruits 的长度。计算并存储数组的前缀和，需要的空间为 O(n)。

解法2：滑动窗口

我们可以换个思路来思考该问题，假设已知区间 [left,right]，现在从起点 startPos 出发，至少需要走多少步才能遍历该区间，实际分为以下三种情况：

1. 当 startPos > right 时，即区间在 startPos 的左边，此时应该从起点开始一直向左移动，直到 left 为止，此时至少需要移动 startPos − left 步；
2. 当 startPos<left 时，即区间在 startPos 的右边，此时应该从起点开始一直向右移动，直到 right 为止，此时至少需要移动 right − startPos 步；
3. 当 left≤startPos≤right 时，即 startPos 刚好在区间范围内，此时有两种选择：

• 从起点开始一直向左移动，直到 left 为止，然后再向右移动到 right，此时需要移动 startPos − left + right − left 步；
• 从起点开始一直向右移动，直到 right 为止，然后再向左移动到 left，此时最少需要移动 right − startPos + right − left 步；
• 根据以上两种情形，最少需要移动 right − left + min⁡( | right − startPos|, | startPos − left|) 步;

​​​​​当然上述所有的情形都可以合并为一个计算公式，

即实际最少需要移动 right − left + min ⁡( |right − startPos|, |startPos − left| ) 步，才能覆盖区间 [left,right]，如下图所示：

我们设函数 step(left, right) 表示从起点 startPos 出发可以覆盖区间 [left,right] 的最少移动步数，此时 step(left, right) = right − left + min⁡(|right − startPos|, |startPos − left|)。

当固定 right 时，此时减少 left，可以观察到:

• 当 left < startPos 时，step(left−1, right) < step(left, right);
• 当 left ≥ startPos 时，step(left−1, right) = step(left, right);

综上可以得到结论：step(left − 1, right) ≤ step(left, right)

即随着 left 的减小，step(left,right) 可能会减小，但一定不会继续增大，利用这个特性我们即可利用滑动窗口来遍历所有符合要求的最大区间，然后找到区间内的覆盖水果的最大值即可，实际计算过程如下:

初始时 left = 0, right = 0，每次 right 向右移动一步；
计算当前区间 [left, right] 需要的移动步数 step，如果 step > k，则我们移动左起点 left，直到满足 step < k, left ≤ right，即可求出移动步数小于等于 k 且以 right 为终点的最长区间，计算出该区间覆盖的水果数目即可；
依次按照上述方式移动直到 right 移动到终点为止。

class Solution {
    public int maxTotalFruits(int[][] fruits, int startPos, int k) {
        int n = fruits.length;
        int sum = 0;
        int ans = 0;
        int left = 0;
        int right = 0;
        while (right < n) {
            sum += fruits[right][1];
            while (left <= right && step(fruits, startPos, left, right) > k ) { 
                sum -= fruits[left][1];
                left++;
            }
            ans = Math.max(ans, sum);
            right++;
        }
            
        return ans;
    }

     private int step(int[][] fruits, int startPos, int left, int right) {
        return fruits[right][0] - fruits[left][0] + 
        Math.min(Math.abs(startPos - fruits[left][0]), 
                Math.abs(startPos - fruits[right][0])); 
    }
}

复杂度分析

• 时间复杂度：O(n)，n 是 数组 fruits 的长度。每次固定窗口的右侧，然后尝试移动左侧窗口，右侧端点最多移动 n 次，左侧端点最多移动 n 次，因此时间复杂度为 O(2n)=O(n)。
• 空间复杂度：O(1)。