MATLAB实现求解最大公因子（欧几里得算法）

BumbleStone

于 2023-02-17 11:30:37 发布

阅读量1.6k

点赞数 1

分类专栏： Matlab 密码学文章标签： matlab 算法开发语言

本文链接：https://blog.csdn.net/m0_56241309/article/details/129082205

版权

Matlab 同时被 2 个专栏收录

11 篇文章

订阅专栏

密码学

10 篇文章

订阅专栏

程序下载链接：https://download.csdn.net/download/m0_56241309/87457277

实验题目：欧几里得算法求解最大公因子

一、实验目的

实验环境： Windows 11操作系统；Matlab2019b

实现目标：欧几里得算法求解最大公因子；

实现交互界面；

实现关键步骤信息输出。

二、方案设计

1. 计算方案

欧几里得算法所依赖的定理为: gcd(a, b)=gcd(b, a-kb)=gcd(b,r)

即反复调用计算gcd，但是需要确保每一次计算之前进行模运算，将大的数字模上小的数字

得到模运算的结果后，再对两个数字使用gcd计算

以此类推，直至其中一个数字在模另一位数字得到0，余下的另一位非零整数即为二者的最大公因子

整体流程在算法上体现为递归运算，因此编写递归函数

2. 信息输出

设置信息输出函数，实现运算界面的信息输出

3. 交互界面

基于Matlab2019b中的mlapp编程实现

三、方案实现

1. 计算过程

介绍：递归函数gcd()

function results = gcd(app,a,b)
            ifb==0
                results=a;
            else
                results=app.gcd(b,mod(a,b));
            end
end

介绍：计算按钮EnButtom回调函数

function EnButtonPushed(app, event)
            ifapp.NUM1.Value==0&&app.NUM2.Value==0
                logRefresh_func(app,'请至少输入一个非零整数');
                return
            end
            
            m=app.NUM1.Value;
            n=app.NUM2.Value;
            app.CF.Value=app.gcd(m,n);
            app.logRefresh_func('求解成功')
            
end

2. 信息输出

介绍：加密界面信息输出函数logRefresh_func

function logRefresh_func(app,StrArrayNew)
            app.Ptime=datestr(now);
            app.LOG=strcat('[',app.Ptime(end-7:end),']');
            StrArrayNew=strcat(app.LOG,StrArrayNew);
            app.StrArray_En=[app.StrArray_En,StrArrayNew,newline];
            app.Process.Value=app.StrArray_En;
end

3. 交互界面

Matlab2019b的mlapp开发环境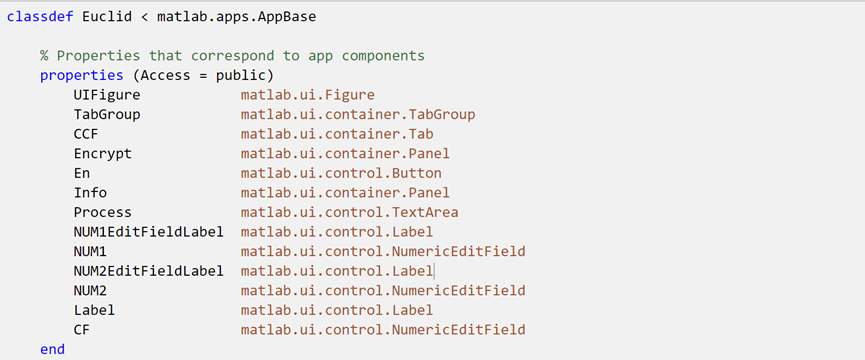

四、数据测试与分析

1. 数据测试

6与3的最大公因子3

8与6的最大公因子2

18与21的最大公因子3

1970与1066的最大公因子2

求解过程

求解演示

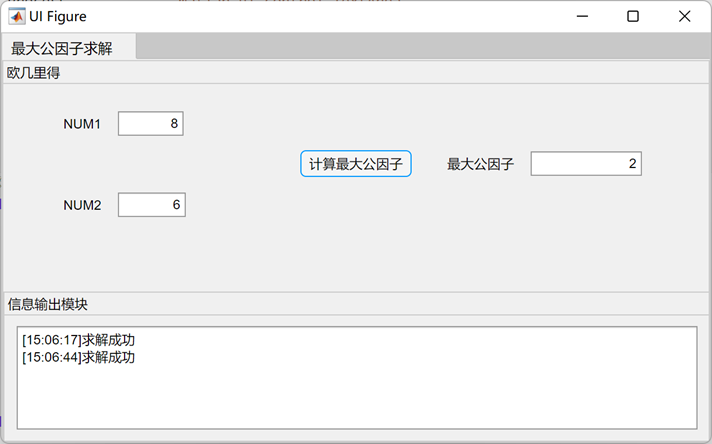
2. 分析

欧几里得算法求解最大公因子与我国古代的更相减损术一样，背后的定理可以描述为：gcd(a, b)=gcd(b, a-kb)=gcd(b,r)，用于求解两个整数的最大公因子。算法本身就是一个递归的过程，在获取到两个整数后，对其使用某一函数，该函数检查两者中较大的数字在模另一位数字后是否为零，如果不为零，则将较大的数字用模运算后得到的结果替换，继续对两个数字使用该函数。这样一直递归下去，直至发现某一次模运算后得到的结果为0，此时可以确定两个数字的最大公因子为余下的非零整数。

五、总结