小黄的刷题之路(十八)——ST表求解区间gcd问题

一、题目

---

二、分析思路

2.1 审题理解

• 区间gcd问题：有n个整数，查询区间的最大公约数。
• 这道题已经提示说数据卡得严，并且给的时间只有1s，而且可以发现给的内存却如此多，这一看就不对劲，我用最简单的做法试了一下
  • 思路：区间gcd其实就转化为递归套娃，比如区间内有三个数a[0] a[1] a[2]，先求gcd(a[0],a[1])得到一个结果记为g，再求gcd(g,a[2])，整个过程也就是$gcd(gcd(a[0],a[1]),a[2])$

#include<bits/stdc++.h> 
using namespace std;
int gcd(int m, int n)
{
	if (n == 0)return m;
	else return gcd(n, m % n);
}
inline int read(){
    int x=0,f=1;
    char ch=getchar();
    while(ch<'0'||ch>'9'){
        ch=getchar();
    }
    while(ch>='0'&&ch<='9'){
        x=(x<<1)+(x<<3)+(ch^48);//x = x*10 + (ch -= '0')
        ch=getchar();
    }
    return x*f;
}
int main( )
{
    int n,m;
    //scanf("%d %d",&n,&m);//cin>>n>>m;
    n = read();m = read();
    int a[n+1];
    for(int i=1;i<=n;i++)a[i]=read();//scanf("%d",&a[i]);//cin>>a[i]
    int l,r;
    while(m--)
    {
        l = read();r = read();//scanf("%d %d",&l,&r);//cin>>l>>r;
        int num=a[l];
        for(int i=l+1;i<=r;i++)num = gcd(a[i],num);
        printf("%d\n",num); 
    }
    return 0;
}

结果不意外地超时了，就算使用快读来加快输入也不行

⭐

TLE(Time Limit Exceed 超时)真的一生之敌

• 暂时是毫无思路了，但是过了一天之后，我再看这题突然区间两个字吸引了我，经过一番查询，发现算法届有个经典的区间最值问题，也就是RMQ问题。

• RMQ问题：对于长度为n的数列A，回答若干询问RMQ(A,i,j)(i,j<=n)，返回数列A中下标在i,j里的最小(大)值

---

2.2 思路

对于RMQ问题，有一个著名的算法叫做ST表，全称Sparse-Table算法，译为稀疏表。是由图灵奖获得者Tarjan提出的。

对于这位大佬，感兴趣的伙伴可以看看这个：tarjan_百度百科 (baidu.com)

ST表是一种解决RMQ问题（区间最值）的强力算法。主要应用倍增的思想，离线预处理时间复杂度$O(nlogn)$，在线查询时间$O(1)$，是一种非常高效的算法，常被称为TLE的死敌，不过ST表的适用场景是有限的，它只能处理静态区间最值，不能维护动态的，也就是说不支持在预处理后对值进行修改

ST表之所以广为使用，不仅因为它的时间复杂度优秀，还因为它的代码思路比较清晰，代码量比较少。核心代码主要集中预处理和查询上

假设现在有长度为n的一个数组a[n]，下面以求数组a的区间最小值为例子

• 离线预处理

设$st[i][j]$表示从第 i 个数起向后连续$2^j$个数中的最小值，也就是$min(a[i],a[i+1],...,a[i+2^j-1])$

一种基于倍增动态规划的思想，其状态转移方程如下：

​ ⭐ $st[i][0]=a[i]$

​ ⭐ $st[i][j]=min(st[i][j-1],st[i+2^{(j-1)}][j-1])$

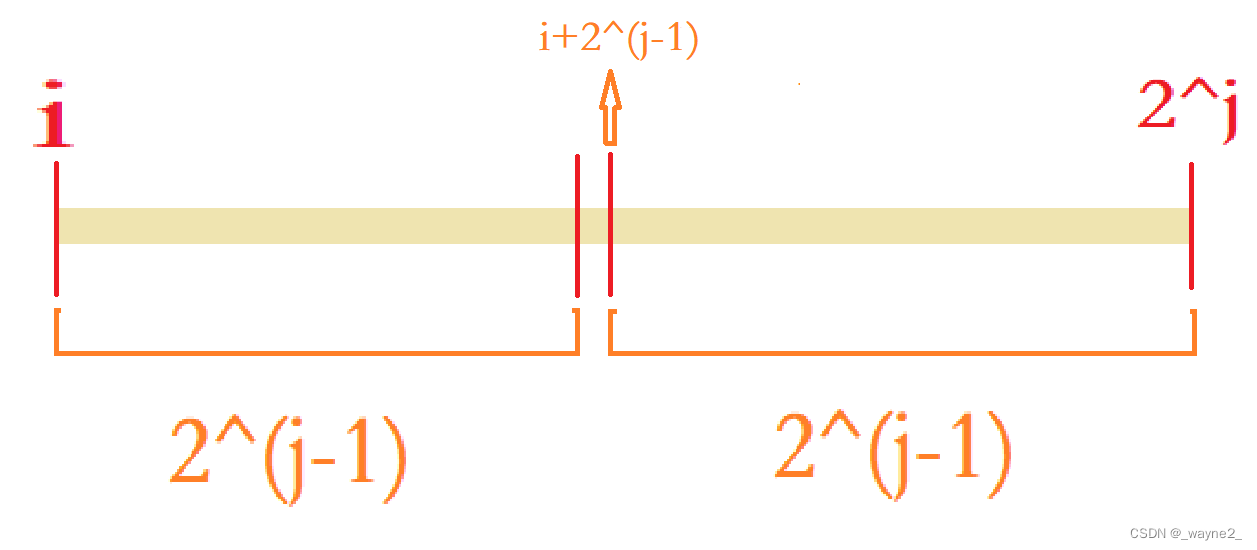
第二条转移方程怎么理解呢，其实就是把区间$a[i\to i+2^j-1]$分成两个左右两个一样长的子区间$a[i\to i+2^{(j-1)}-1]$和$a[i+2^{(j-1)}\to i+2^j-1]$，那么整个大区间的最小值就是两个已计算过的区间最小值的最小值。（有点像分治法的思想，一分为二，化大为小）

int Log[n+1];//以2为底的对数数组
Log[1]=0;
for(int i=2;i<=n;i++)
    Log[i]=Log[i/2]+1;

int n,m;
cin>>n>>m;//数组长度和查询次数
for(int i=1;i<=n;i++)
{
    cin>>a[i];
    st[i][0]=a[i];
}
for(int j=1;j<=Log[n];j++)
    for(int i=1;i<=n;i++)
        st[i][j]=min(st[i][j-1],st[i+(1<<j-1)][j-1]);

热知识：位移运算符的优先级是最低的，低于加减运算符，先计算加减再进行位移

• 在线查询

假设每次查询的区间左端点为 l 右端点为 r ,思路是，首先找到一个值k，k的含义是“最大的$2^k$不超过查询区间长度$l-r+1$”，比如$l=1,r=9$，此时区间长度为9，那么k最大为3，再大一点比如k=4，$2^4=16$超过了区间长度9，所以k=4不行，k=3可以。很显然，$k=lo{g}_2(r-l+1)$满足我们对k的要求

为什么这么做呢？，因为这样子我们可以找两个长度为$2^k$的区间，一个以l为左端点，另一个以r为右端点，对于k的要求使得这两个区间合起来一定覆盖查询区间，甚至会有重叠部分，那么我们对这两个区间分别求最小值，再比较两个最小值，更小的那个就是整个大区间的最小值。（要注意重叠的部分是不会影响区间最小值的）

我们用式子来看看这个过程，查询区间是$a[l\to r]$，把其分成两个区间$a[l\to l+2^k]$ 和 $a[r-2^k\to r]$，那么根据上面的我们的解释可以得到：

m i n ( a [ l → r ] ) = m i n { m i n ( a [ l → l + 2 k ] ) , m i n ( a [ r − 2 k → r ] ) } min(a[l \rightarrow r]) = min\{min(a[l\rightarrow l+2^k]),min(a[r-2^k \rightarrow r])\} min(a[l→r])=min{min(a[l→l+2k]),min(a[r−2k→r])}

这时候就能利用前面离线预处理的结果，直接取出ST表里的数据比较得出答案

$min(a[l\to r])=min(st[l][k],st[r-2^k+1][k])$

int Log[n+1];
Log[1]=0;
for(int i=2;i<=n;i++)
    Log[i]=Log[i/2]+1;
int query(int l,int r)
{
    int k=Log[r-l+1];
    return min(st[l][k],st[r-(1<<k)+1][k]);
}

这里可能会有同学不理解为啥要设置一个Log数组，似乎有点多此一举，但其实这也是一种优化时间复杂度的预处理手段，因为一旦查询次数多了之后，每次查询都要计算一次log，就非常花时间了，一次性把log从1到n的结果都以递推的方式计算好给存起来，后面直接取数据，就方便了很多，这种离线预处理+在线查询的思想是十分值得我们学习借鉴的

讲到这里，你可能会觉得，哎说了半天你一句gcd也不提，是不是跑题了，其实不是的，ST表不仅能处理区间最值问题，凡是符合结合律且可重复贡献的信息查询都可以使用ST表高效进行。可重复贡献的意义在于，可以对两个交集不为空的区间进行信息合并，显然最大值、最小值、最大公约数、最小公倍数、按位或、按位与都符合这个条件。

那么只需要写一个求最大公约数的gcd函数，然后把我们上面的min全给改成gcd就行了

int gcd(int a,int b)//辗转相除法
{
    if(!b) return a;
    else return gcd(b,a%b);
}

为了加快输入输出，我使用了一些网上找的模板，基本都是一些固定的写法，可以收藏到自己的代码库里，以后遇到卡时间的题目，直接套用即可
感兴趣的同学可以看看这篇文章，十分详细：浅谈C++ IO优化——读优输优方法集锦

---

三、代码实现

3.1. C++实现

#include<bits/stdc++.h>
using namespace std;
const int maxn=200000;
//优化输入输出=============================
inline char nc() 
{
	static char buf [100000],*p1=buf,*p2=buf;
	return p1==p2&&(p2=(p1=buf)+fread(buf,1,100000,stdin),p1==p2)?EOF:*p1++;
}
inline int read() 
{
	static char c=nc(); int x=0,f=1;
	for(;c>'9'||c<'0';c=nc()) if(c=='-') f=-1;
	for(;c<='9'&&c>='0';c=nc()) x=(x<<3)+(x<<1)+c-48;
	return x*f;
}
inline void write(int x) {//加快输出
   if(x>9) write(x/10);  
   putchar(x%10+'0');  
}
//=========================================
int gcd(int a,int b)//辗转相除法
{
    if(!b) return a;
    else return gcd(b,a%b);
}
///st[i][j] 表示从位置i开始，2^j个元素的最大公约数
int st[maxn][20],a[maxn];//区间长度最大不超过2^20
int Log[maxn];
int query(int l,int r)
{
    int k=Log[r-l+1];
    return gcd(st[l][k],st[r-(1<<k)+1][k]);
}

int main()
{
    //离线预处理
    //2^Log[i]=i  Log[i] = log2(i)
    Log[1]=0;
    for(int i=2;i<maxn;i++)
        Log[i]=Log[i/2]+1;
    int n,m;
    n=read();
    m=read();       
    for(int i=1;i<=n;i++)
    {
        a[i]=read();
        st[i][0]=a[i];
    }
    for(int j=1;j<=Log[n];j++)
    {
        for(int i=1;i<=n;i++)
        {
            st[i][j]=gcd(st[i][j-1],st[i+(1<<j-1)][j-1]);
        }
    }
    //在线查询
    while(m--)
    {
        int l,r;
        l=read(),r=read();
        write(query(l,r));
        printf("\n");
    }
    return 0;
}

---

四、总结

• 真的很佩服这位能够想出ST表算法的计算机科学家，ST表的关键词是“离线预处理+在线查询”，“倍增动态规划”，“静态算法”，其中的思想非常值得我们借鉴和学习，这次的题目也让我收益匪浅

---

⭐感谢您能看到这里，这是对我莫大的鼓励！⭐