算法
1. 算法基础
1.1 算法效率
算法效率得主要指标是基本操作次数的增长次数。包含最差效率,最优效率,平均效率(输入具有随机性)和摊销效率(同样的数据结构执行多次操作,然后分摊到每一次上)。
1.2 渐进符号O,Ω,Θ
- 1.2.1 符号O
O表示上界,定义为:对于足够大的n,t(n)的上界由g(n)的常数倍来确定,即:t(n) ≤ cg(n),c为常数,记为 t ( n ) ∈ O ( g ( n ) ) t(n) \in O(g(n)) t(n)∈O(g(n))
-1.2.1 符号Ω
Ω表示下界,定义为:对于足够大的n,t(n)的下界由g(n)的常数倍来确定,即:t(n) ≥ cg(n),c为常数,记为
t
(
n
)
∈
Ω
(
g
(
n
)
)
t(n) \in \Omega(g(n))
t(n)∈Ω(g(n))
-1.2.3 紧界Θ
Θ
\Theta
Θ表示紧界,定义为:对于足够大的n,t(n)的上界和下界由g(n)的常数倍来确定,即:
c
2
g
(
n
)
≤
t
(
n
)
≤
c
1
g
(
n
)
c_{2}g(n) \le t(n) \le c_{1}g(n)
c2g(n)≤t(n)≤c1g(n),c为常数,记为
t
(
n
)
∈
Θ
(
g
(
n
)
)
t(n) \in \Theta(g(n))
t(n)∈Θ(g(n))
当算法由两个连续执行的部分组成时,该算法的整体效率由具有较大增长次数的那部分所决定。
1.3 运算规则
- O ( f ) + O ( g ) = O ( m a x f , g ) O(f) + O(g) = O(max{f, g}) O(f)+O(g)=O(maxf,g)
- O ( f ) + O ( g ) = O ( f + g ) O(f) + O(g) = O(f+g) O(f)+O(g)=O(f+g)
- O ( f ) ∗ O ( g ) = O ( f ∗ g ) O(f) * O(g) = O(f * g) O(f)∗O(g)=O(f∗g)
- 如 果 g ( n ) = O ( f ( n ) ) , 则 O ( f ) + O ( g ) = O ( f ) 如果g(n) = O(f(n)),则O(f) + O(g) = O(f) 如果g(n)=O(f(n)),则O(f)+O(g)=O(f)
- O ( c f ( n ) ) = O ( f ( n ) ) O(cf(n)) = O(f(n)) O(cf(n))=O(f(n))
- f = O ( f ) f = O(f) f=O(f)
1.4 求解递归问题的时间复杂度
1.4.1 迭代方法
指循环的展开递归方程,把递归方程转化为和式,然后使用求和技术求解
1.4.2 Master主定理
求解 T ( n ) = a T ( n b ) + f ( n ) , a ≥ 1 , b > 0 是 常 数 , f ( n ) ≥ 0 T(n) = aT(\frac{n}{b}) + f(n), a \ge 1, b>0是常数, f(n) \ge 0 T(n)=aT(bn)+f(n),a≥1,b>0是常数,f(n)≥0型方程
- 若 f ( n ) ≤ n l o g b a f(n) \le n^{log_{b}{a}} f(n)≤nlogba, 则 T ( n ) = Θ ( n l o g b a ) T(n) = \Theta(n^{log_{b}{a}}) T(n)=Θ(nlogba)
- 若 f ( n ) = n l o g b a f(n) = n^{log_{b}{a}} f(n)=nlogba, 则 T ( n ) = Θ ( n l o g b a l g n ) T(n) = \Theta(n^{log_{b}{a}} lg{n}) T(n)=Θ(nlogbalgn)
- 若 f ( n ) ≥ n l o g b a f(n) \ge n^{log_{b}{a}} f(n)≥nlogba,且对于所有充分大的n, a f ( n / b ) ≤ c f ( n ) af(n/b) \le cf(n) af(n/b)≤cf(n),则 T ( n ) = Θ ( f ( n ) ) T(n) = \Theta(f(n)) T(n)=Θ(f(n))
1.5 习题

3
2. 分治法
将一个规模为n的问题分解为k个规模较小的子问题,这些子问题互相独立且与原问题的形式相同,递归的解决这些子问题,然后将各子问题的解合并得到原问题的解。
2.1 分治法适用的情况
分治能处理的问题具有以下特征
- 问题规模缩小到一定程度容易解决
- 问题可以分解为若干个规模较小的相同问题,即问题具有最优子结构性质。
- 子问题的解可以合并为该问题的解
- 各个子问题相互独立
特征二是应用分治法的前提,此特征反映了递归思想的应用。
特征三是关键,能否使用分治法完全取决于此特征。如果仅具有一二特征而不具备特征三,则则应使用贪心法或动态规划。
特征四涉及到算法的效率,如果子问题不独立则会重复的解决公共子问题,应交给动态规划
2.2 伪代码
Divide-and-Conquer(P)
#输入:待解决问题P
#输出:以解决的问题T
if |P| < n0:
# 如果问题规模足够小
then return(ADHOC(P))
# 否则将问题分解为i个Pi
for i <- 1 to k:
do yi <- Divide-and-Conquer(Pi)
T <- Merge(y1, y2, y3, ..) # 合并子问题
return(T)
计算时间
分成两个子问题的计算时间:
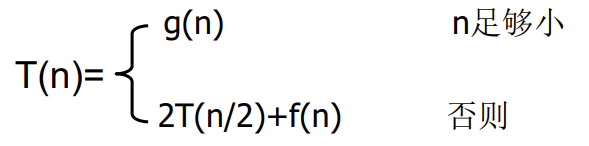
- g(n) 是足够小的问题规模直接计算出答案的时间
- f(n) 是合并的计算时间 (Master主定理)
2.3 归并排序
算法 MergeSort(A[0, ...n-1])
# input: 无序数组
# output: 有序数组
copy A[0...[n/2]-1] to B[0...[n/2]-1];
copy A[[n/2]...n] to C[0...[n/2]-1];
Mergesort(B[0...[n/2]-1]);
Mergesort(C[0...[n/2]-1]);
Merge(B, C, A)
return A
# 合并操作
Merge(B, C, A)
# input: B[0...p-1],C[0...q-1],A[0...p+q-1]
# output: A
i<-0, j<-0, k<-0
while i<p & j<q:
if B[i] < C[p]{
then A[k] <- B[i];
i<i+1;
}
else{
A[k] <- C[j];
j<-j+1;
}
k<-k+1;
if i = p:
copy C[j...q-1] to A[k...p+q-1];
else:
copy B[i...p-1] to A[k...p+q-1];
归并排序最优最差都是O(nlogn), 辅助空间为O(n)
2.4 最大最小值
问题:给定一个数组,求出其中的最大值和最小值。按照常规操作,需要两次n-1次的比较,使用分治法可以使比较次数降低到3n/2 - 2。
核心思想:将数组不断分解,合并时只合并每组的最大最小值
算法 MaxMin(A)
# input: A[i...j]
# output: max and min
if i = j then return A[i], A[i]
if j = i +1 then
if A[i]<A[j] return A[i], A[j]
else
return A[j], A[i]
k<- j-i+1 / 2
m1, M1 <- MaxMin(A[i:k])
m2, M2 <- MAxMin(A[k+1:j)
m<-min(m1, m2)
M<-max(M1, M2)
return m, M
2.5 快速排序
最优为O(nlogn), 最次为O( n 2 n^{2} n2)。
算法 quicksort(A)
// 输入:待排数组A,切片索引start, end
// 输出:有序数组
left<-start; right<-end;
center <- A[left]
while left<right:
while left<right & A[right]>center: # 先动右指针
right -= 1
A[left] = A[right]
while left<right & A[left] < center:
left+=1
A[right] = A[left]
A[left] = center
quicksort(A, start, left-1)
quicksort(A, left+1, end)
快排的最内循环效率非常高,在处理随机排列数组时,速度比合并排序快。
三平均分区速度更快
2.6 折半查找
找到数据并返回索引值
算法 BinarySearch(A[0...n-1], s)
//输入:有序数组
//输出:索引
start <-0, end<-n-1;
while start < end:
mid <- (start + end) // 2
if A[mid] = s then return mid
elif A[mid]<s then start<-mid+1
else end <- mid-1
2.7 大整数乘法
计算n位二进制整数X和Y的乘积,给出一个复杂度为
O
(
n
1.59
)
O(n^{1.59})
O(n1.59)的算法。算法的思想是,将X和Y分成n/2位。

其中
A
D
+
B
C
=
(
A
+
B
)
(
C
+
D
)
−
A
C
−
B
D
AD+BC = (A+B)(C+D) - AC - BD
AD+BC=(A+B)(C+D)−AC−BD
2.8 Strassen矩阵乘法
计算两个二阶矩阵乘法的算法。只用了七次乘法运算但增加了加、减法的运算次数

2.9 线性时间选择
给定n个元素和一个整数k, 1 ≤ k ≤ n 1 \le k \le n 1≤k≤n,要求找出n个元素中第k小的元素。
…
2.10 DFT & FFT
FFT问题浅显的讲,是给定一组 a 0 , a 1 , . . . . a n − 1 , 其 中 n = 2 t , t 为 正 整 数 a_{0}, a_{1}, ....a_{n-1},其中n = 2^{t}, t为正整数 a0,a1,....an−1,其中n=2t,t为正整数,根据公式 A i = ∑ k = 0 n a k e 2 i k π n j , j 是 虚 数 单 位 A_{i} = \sum^{n}_{k=0}{a_{k}e^{\frac{2ik\pi}{n}j}}, j是虚数单位 Ai=∑k=0naken2ikπj,j是虚数单位计算每个 A i A_{i} Ai的题目。使用蛮力法直接计算的时间复杂度为 Θ ( n 2 ) \Theta(n_{2}) Θ(n2),使用分治法可以降到 n l o g n nlogn nlogn。
首先引入DFT(离散傅里叶变换)概念。n阶多项式可以用n+1个点值对来表示,也就是说确定了n+1个点就确定了n阶多项式。 { P 0 ( x ) P 1 ( x ) . . . P n ( x ) } = { 1 x 0 x 0 2 . . . x 0 n 1 x 1 x 1 2 . . . x 1 n . . . . . . . . . . . . . . . 1 x n x n 2 . . . x n n } { p 0 p 1 . . . p n } \left\{ \begin{matrix}P_{0}(x) \\ P_{1}(x) \\ ... \\ P_{n}(x) \end{matrix} \right\} = \left\{ \begin{matrix} 1 & x_{0} & x_{0}^{2} & ... & x_{0}^{n} \\ 1 & x_{1} & x_{1}^{2} & ... & x_{1}^{n} \\ ... & ... & ... & ... & ... \\ 1 & x_{n} & x_{n}^{2} & ... & x_{n}^{n} \end{matrix} \right\} \left\{ \begin{matrix} p_{0} \\ p_{1} \\ ... \\ p_{n} \end{matrix} \right\} ⎩⎪⎪⎨⎪⎪⎧P0(x)P1(x)...Pn(x)⎭⎪⎪⎬⎪⎪⎫=⎩⎪⎪⎨⎪⎪⎧11...1x0x1...xnx02x12...xn2............x0nx1n...xnn⎭⎪⎪⎬⎪⎪⎫⎩⎪⎪⎨⎪⎪⎧p0p1...pn⎭⎪⎪⎬⎪⎪⎫。这就是离散傅里叶变换,其本质就是矩阵M和向量X做点乘。
2.10.1 FFT —— 快速傅里叶变换
分治法减少计算量的操作体现在将多项式转换成点值表示这一步,利用的是函数的对称性。
计算式 A ( x ) = a 0 + a 1 x 1 + a 2 x 2 2 + . . . + a n x n n , n 是 2 的 倍 数 A(x) = a_{0} + a_{1}x_{1} + a_{2}x_{2}^{2} + ... + a_{n}x_{n}^{n},n是2的倍数 A(x)=a0+a1x1+a2x22+...+anxnn,n是2的倍数,奇数项是偶函数,偶数项是奇函数,而奇数项可以分离成x乘以一个偶函数。
在DFT中提到,n阶多项式需要计算n+1个点。傅里叶提出,使用n+1个复数来代替n+1个x变量。因为函数存在奇偶性,所以原本需要的n个点,现在只需n/2个点(根据奇偶性可以求出相反符号的值),但这样做的前提是正负对一定存在,实数域上无法保证这一点,因此引入复数域。这n个复数域的点并不是随机选取的,而是在复平面将单位圆等分n分后对应的点。
同样对于计算式 A ( x ) = a 0 + a 1 x 1 + a 2 x 2 2 + . . . + a n x n n A(x) = a_{0} + a_{1}x_{1} + a_{2}x_{2}^{2} + ... + a_{n}x_{n}^{n} A(x)=a0+a1x1+a2x22+...+anxnn,整理得
- A e v e n ( x ) = a 0 + a 2 x 2 + a 4 x 4 + . . . + a n − 2 x n − 2 2 A_{even}(x) = a_{0} + a_{2}x^{2} + a_{4}x^{4} + ... + a_{n-2}x^{\frac{n-2}{2}} Aeven(x)=a0+a2x2+a4x4+...+an−2x2n−2
- A o d d ( x ) = a 1 + a 3 x 2 + a 5 x 4 + . . . + a n − 1 x n − 2 2 A_{odd}(x) = a_{1} + a_{3}x^{2} + a_{5}x^{4} + ... + a_{n-1}x^{\frac{n-2}{2}} Aodd(x)=a1+a3x2+a5x4+...+an−1x2n−2
进一步整理可以发现 A ( x ) = A 1 ( x 2 ) + x A 2 ( x 2 ) A(x) = A1(x^{2}) + xA2(x^{2}) A(x)=A1(x2)+xA2(x2)。 根据复平面单位圆的特点,得到 ω n k + n 2 = − ω n k \omega_{n}^{k + \frac{n}{2}} = -\omega_{n}^{k} ωnk+2n=−ωnk。
综上所述,在
0
≤
i
≤
n
2
0 \le i \le \frac{n}{2}
0≤i≤2n的部分有
A
(
x
i
)
=
A
1
(
x
i
2
)
+
x
i
A
2
(
x
i
2
)
A(x_{i}) = A1(x_{i}^{2}) + x_{i}A2(x_{i}^{2})
A(xi)=A1(xi2)+xiA2(xi2)
在
n
2
≤
i
≤
n
\frac{n}{2} \le i \le n
2n≤i≤n的部分
A
(
x
i
+
n
2
)
=
A
(
−
x
i
)
=
A
1
(
x
i
2
)
−
x
i
A
2
(
x
i
2
)
A(x_{i+\frac{n}{2}}) = A(-x_{i}) = A1(x_{i}^{2}) - x_{i}A2(x_{i}^{2})
A(xi+2n)=A(−xi)=A1(xi2)−xiA2(xi2)
2.10.2 FFT实现
# ------------------
# DFT & FFT
# ------------------
def DFT(x):
x = np.asarray(x, dtype=float) # 浅拷贝
N = x.shape[0]
M = [[j for j in range(N)] for j in range(N)]
M = np.asarray(M, dtype=complex)
w = np.exp(-2j * np.pi / N)
for i in range(N):
for j in range(N):
M[i][j] = np.power(w,i*j)
return np.dot(M, x)
def FFT(x):
x = np.asarray(x, dtype=float)
N = x.shape[0]
if N < 2:
return DFT(x)
even_x = FFT(x[0::2])
odd_x = FFT(x[1::2])
coeff = np.exp(-2j * np.pi * np.arange(N) / N)
return np.concatenate([
even_x + coeff[:int(N/2)] * odd_x,
even_x + coeff[int(N/2)] * odd_x
])
2.11 循环赛日程表
问题:有 n = 2 k n = 2^k n=2k个运动员进行循环赛,设计一个可以满足以下条件的比赛日程表
- 每个选手必须与其他n-1个选手各赛一次
- 每个选手一天只能赛一次
- 循环赛一共进行n-1天
思路:n个选手的日程可以由另外n/2个选手确定。所以问题可以被分治地解决。拿k=3举例,问题一共需要4步。
- 初始化第一个选手的日程
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|
- 第二行根据第一行填充
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|
| 2 | 1 | 4 | 3 | 6 | 5 | 8 | 7 |
- 第三、四行根据第一二行填充
- 第五、六、七、八行根据前四行填充
具体填充的过程也是分治的实现。执行第二步骤的时候将问题划分为四块

执行第三步的时候将问题划分为两块

最后一步合为一块

实现
%%time
# ---------------------
# 循环赛日程表
# ---------------------
def create(N):
M = np.asarray([np.zeros(N+1) for j in range(N+1)])
# init
for t in range(1, N+1):
M[1][t] = t
m=1; # m表示填充起始行;n用于分治思想
n = N
k = 1
while n>1:
n/=2
k+=1 # 求lgN
for p in range(1, k+1): # 分成k组 k = log N
N = int(N / 2)
for q in range(1, N+1): # 分治
for i in range(m+1, 2*m+1):
for j in range(m+1, 2*m+1):
M[i][j + (q-1)*m*2] = M[i - m][j + (q-1)*m*2 - m]
M[i][j + (q-1)*m*2 - m] = M[i - m][j + (q-1)*m*2]
m *= 2
m = int(m/2)
for ii in range(1, m+1):
print("第%d位选手:" % ii, end=" ")
for jj in range(2, m+1):
# print(jj)
print(M[ii][jj], end=" ")
print(end="\n")
create(8)
3. 动态规划
动态规划类似分治,也是将待求问题分解成若干个子问题。分治法的弱点是会重复计算子问题的不独立部分,消耗了不必要的效率。如果能够保存已解决的子问题的答案,而在需要时再找出已求得的答案,就可以避免大量重复计算,从而得到多项式时间算法。因此,动态规划是用来解决多段决策过程最优的通用方法。
动态规划的使用条件有
- 最优子结构 : 问题最优解等价于子问题最优解之和
- 无后向性: 每个状态都是历史状态的完整总结
- 子问题的重叠性: 子问题不独立
动态规划的核心思想:分治和解决冗余
3.1 矩阵连乘
输入n个矩阵,计算 A 1 × A 2 × . . . . × A n A_{1} \times A_{2} \times .... \times A_{n} A1×A2×....×An过程中,乘法运算次数最少的乘法。
例如计算 A 1 = 10 × 100 , A 2 = 100 × 5 , A 3 = 5 × 50 A_{1} = 10 \times 100, A_{2} = 100 \times 5, A_{3} = 5 \times 50 A1=10×100,A2=100×5,A3=5×50时,$(A_{1} \times A_{2}) \times A_{3} 需 要 7500 次 乘 法 运 算 , 而 需要7500次乘法运算,而 需要7500次乘法运算,而A_{1} \times (A_{2} \times A_{3}) $则需要75000次计算。
实现
使用一个二维矩阵记录最优结构。
算法 MultiMatrix(p[0, 1, ..., n])
//输入:n个可以连乘的矩阵的行列值,Ai的行是pi, 列是pi+1
//输出:最少计算次序
n <- len(p)-1
init m[n][n]<-[0]; path[n][n]<-[0]
for r<-2 to n: # 表示进行连乘的矩阵个数
for i<-0 to n-r+1: # 表示连乘矩阵的左边界
j <- r+i-1 # 右边界
m[i][j] <- m[i+1][j] + p[i] * p[i+1] * p[j+1]
path[i][j] <- i+1
for k<-i+1 to j-1: # 断点位置
t <- m[i][k] + m[k+1][j] + p[i] * p[k+1] * p[j+1]
if t < m[i][j] then m[i][j] <- t; path[i][j] <- k
算法 traceback(path, i, j)
//输入:路径矩阵,左边界,右边界
//输出:连乘表达式
size <- j-i+1
if size = 1 then return "Ai"
k<- path[i][j] - 1 # 因为path中不是从0开始的
res <- res + "(" + traceback(path, i, k)
res <- res + traceback(path, k+1, j) + ")"
return res
3.2 最长公共子序列
…
实现
# -------------------
# 最长公共子序列
# -------------------
X = 'ABCBDAB'
Y = 'BDCABA'
def longest(x, y):
m = np.asarray([np.zeros(len(y)) for j in range(len(x))])
m[0][0] = (x[0] == y[0])
for i in range(1, m.shape[0]):
flag = (x[i] == y[0])
m[i][0] = (m[i-1][0] or flag)
for j in range(1, m.shape[1]):
flag = (x[0] == y[j])
m[0][j] = (m[0][j-1] or flag)
for i in range(1, m.shape[0]):
for j in range(1, m.shape[1]):
flag = (x[i] == y[j])
m[i][j] = m[i-1][j] + flag if (m[i-1][j] + flag >= m[i][j-1] + flag) else m[i][j-1] + flag
print(m)
return m[-1][-1], m
length, path = longest(X, Y)
3.3 二项式系数
实现
# --------------
# 二项式系数
# C(n, k)
# (a+b)^n = C(n,0)a^n + ... + C(n,n)b^n
# 给定n,用一个二维矩阵存储所有C(n,k)
# --------------
def Binomial(n:int):
c = np.array([np.zeros(n+1) for j in range(n+1)])
c[0][0] = 1
for i in range(1, n+1):
c[i][i] = 1
c[i][0] = 1
# n作行, k作列 ,且 n>=k
for i in range(2, n+1):
for j in range(1, i):
c[i][j] = c[i-1][j-1] + c[i-1][j]
print(c)
Binomial(5)
3.4 多段图
。。。。
3.5 Floyd算法
。。。。
3.6 传递闭包——Warshall
。。。
3.7 最优二叉查找树
。。。
3.8 0,1背包
。。。
3.9 TSP动态规划
。。。
3.10 曼哈顿
实现
# --------------
# 曼哈顿游客问题
# 在加权网络中寻找一条最长的路线
# --------------
import numpy as np
C = [
[[0, 0], [3, 0], [2, 0], [4, 0], [0, 0]],
[[0, 1], [3, 0], [2, 2], [4, 4], [2, 3]],
[[0, 4], [0, 6], [7, 5], [3, 2], [4, 1]],
[[0, 4], [3, 4], [3, 5], [0, 2], [2, 1]],
[[0, 5], [1, 6], [3, 8], [2, 5], [2, 3]],
]
C = np.array(C)
def Manhattan(C:np.array):
# s记录各点权重
s = np.array([np.zeros(5) for j in range(5)])
# p记录各点动作
# 0表示向右 1表示向下
p = np.array([np.zeros(5) for j in range(5)])
# init
s[0][0] = 0
for i in range(1, 5):
s[i][0] = s[i-1][0] + C[i][0][1]
p[i][0] = 1
s[0][i] = s[0][i-1] + C[0][i][0]
p[0][i] = 0
# DP
for i in range(1, 5):
for j in range(1, 5):
# 从上面来
s[i][j] = s[i-1][j] + C[i][j][1]
p[i][j] = 1
if s[i][j] < (s[i][j-1] + C[i][j][0]):
s[i][j] = s[i][j-1] + C[i][j][0]
p[i][j] = 0
print(p)
return s[-1][-1], p
def trace(p:np.array, i:int, j:int):
if i==0 and j==0:
print('(1, 1)')
return
print('({}, {}) ->'.format(i+1, j+1), end=' ')
if p[i][j] == 1:
trace(p, i-1, j)
else:
trace(p, i, j-1)
trace(path, 4, 4)
3.11 最大子段和
给定n个整数构成的序列 < a 1 , a 2 , . . . , a n > , a i 可 以 是 负 数 <a_{1}, a_{2}, ..., a_{n}>, a_{i}可以是负数 <a1,a2,...,an>,ai可以是负数。求解 m a x { 0 , max 1 ≤ i ≤ j ≤ n ∑ k = i j a k } max \{0, \max_{1 \le i \le j \le n} \sum_{k=i}^{j}{a_{k}}\} max{0,max1≤i≤j≤n∑k=ijak}。
实例:<-2, 11, -4, 13, -5, -2>
最大子段和:
a
2
+
a
3
+
a
4
=
20
a_{2} + a_{3} + a_{4} = 20
a2+a3+a4=20
思路:使用一个一维列表保存路径,求前向最大子段和
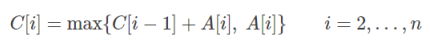
实现
# ---------------
# 最大子段和
# ---------------
def MaxChild(A:np.array):
n = A.shape[0]
C = np.asarray([i for i in range(n+1)])
C[1:] = A
path = [[]]
for i in range(n):
if C[i+1] >= (C[i+1] + C[i]):
C[i+1] = C[i+1]
path.append([i+1])
else:
C[i+1] = C[i+1] + C[i]
x = copy.deepcopy(path[i])
x.append(i+1)
path.append(x)
m = C[0]
for j in range(1, n+1):
if m < C[j]:
m = C[j]
k = j
return C, path, k
a = np.asarray([-2, 11, -4, 13, -5, -2], dtype=int)
C, path, k = MaxChild(a)
print("path: ", path[k])
print("value: ", C[k])
结果

4. 红黑树
。。。
5. 贪心算法
在贪心算法中采用逐步构造最优解的方法,在每个阶段都做出看上去最优的决策,且决策一旦做出则不可更改。贪心算法希望通过局部最优得到全局最优。
贪心算法是否产生优化解需严格证明。
- 贪心选择性:全局最优可以通过局部最优得到
- 优化子结构:一个优化解包括子问题的优化解
- 伪码
算法 GREEDY(A, n)
//in: 问题A,有n个子问题
solution = T
for i<-1 to n
x = SELECT(A) //贪心选择局部解
if FEASIBLE(solution, x) // 可行解
then solution = solution + x // 合并解
return solution
5.1 活动安排问题
问题:设S = {1, 2, …, n}是n个活动的集合,每个活动使用一个资源(比如时间),每个资源只能为一个活动所用。每个活动 i i i有一个起始时间 s i s_{i} si和结束时间 f i f_{i} fi,且满足 s i ≤ f i s_{i} \le f_{i} si≤fi。称活动 i , j i, j i,j是相容的,若 s i ≥ f j 或 s j ≥ f i s_{i} \ge f_{j} 或 s_{j} \ge f_{i} si≥fj或sj≥fi。
实现
def greedyselect(s:list, f:list, A:list):
A[1] = True
j = 1
for i in range(2, n+1):
if s[i] >= f[j]:
A[i] = True
j = i
else:
A[i] = False
活动安排问题的优化子结构
设S = {1, 2, …, n}是n个活动的集合, [ s i , f i ] [s_{i}, f_{i}] [si,fi]是活动i的起始终止时间,且 f 1 ≤ f 2 ≤ . . . ≤ f n f_{1} \le f_{2} \le ... \le f_{n} f1≤f2≤...≤fn,设A是S的调度问题的一个优化解且包含活动 1 1 1, 则A’ = A - {1}是 S ′ = i ∈ s ∣ s i ≥ f 1 S' = {i \in s | s_{i} \ge f_{1}} S′=i∈s∣si≥f1的优化解。显然,A’中的活动都是相容的,仅需要证明A’是最大的。
使用反证法证明。假设存在一个S’的优化解B’, |B’| > |A’|,令B = {1} ∪ B’,对于 ∀ i ∈ S ′ , s i ≥ f 1 , B 中 活 动 相 容 \forall i \in S', s_{i} \ge f_{1}, B中活动相容 ∀i∈S′,si≥f1,B中活动相容, 由于|A’| = |A| - 1, |B| = |B’| + 1 > |A’| + 1 = |A|,这与|A|最大矛盾、故优化子结构满足
活动安排问题的贪心选择性
设 l i l_{i} li是 S i = j ∈ S ∣ s j ≥ f i − 1 S_{i} = {j \in S | s_{j} \ge f_{i-1}} Si=j∈S∣sj≥fi−1中具有最小结束时间 f l i f_{li} fli的活动 l i l_{i} li。设A是S的包含活动1的优化解,其中 f 1 ≤ . . . ≤ f n f_{1} \le ... \le f_{n} f1≤...≤fn,则 A = ⋃ i = 1 k { l i } A = \bigcup^{k}_{i=1}{\{l_{i}\}} A=⋃i=1k{li}是一个最优解(最终解是所有f最小的相容活动的集合)。
使用归纳法证明。当|A|=1时显然成立。设|A| < k时,命题成立。当|A|=k时,根据优化子结构的性质( A = 1 ⋃ A j , A j 是 S j = j ∈ S ∣ s j ≥ f 1 A = {1} \bigcup A_{j}, A_{j}是S_{j} = {j \in S | s_{j} \ge f_{1}} A=1⋃Aj,Aj是Sj=j∈S∣sj≥f1的优化解),于是 A = 1 ⋃ A 1 ′ = ⋃ i = 1 k l i A = {1} \bigcup A'_{1} = \bigcup_{i=1}^{k}{l_{i}} A=1⋃A1′=⋃i=1kli





















 163
163











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








