《数据挖掘》第七课笔记

---

一、确定性图灵机模型

  在确定性图灵机（DTM）中，其控制规则规定了在任何给定情况下最多只能执行一个动作。

  确定性图灵机具有转换功能，对于磁带头下的给定状态和符号，该转换功能指定了三件事：1、要写入磁带的符号，2、头部应移动的方向（向左，向右或都不向），3、有限控制的后续状态。

  例如，状态3的磁带上的X可能会使DTM在磁带上写Y，将磁头向右移动一个位置，然后切换到状态5。

---

二、概率机（非确定性）模型

  在理论计算机科学中，非确定性图灵机（NTM）是一种理论计算模型，其控制规则在某些给定情况下指定了多个可能的动作。 也就是说，NTM的下一个状态不是完全由其动作和它所看到的当前符号决定的（不同于确定性图灵机）。给定一个初始状态，每一步执行的时候机器有多个选择可以执行

  例如，状态3的磁带上的X可能允许NTM：输入Y，向右移动，然后切换到状态5或者写一个X，向左移动，并停留在状态3。
  或者想象在曼哈顿东西南北格点化的街道中有一个小醉汉，他每次到达一个交叉路口时都会随机选择前后左右四个方向其中的一个，然后继续前进（或后退）；在走到下一个路口时又随机选择一次方向……如此继续下去。

  所以对于非确定图灵机的下一步的选择具有不确定性，但实际上NTM足够幸运，它总是会选择那个能够最终指向接受状态的那一步。

---

三、确定性图灵机模型与概率机（非确定性）模型

   DTM遵循的是单个“计算路径”，而NTM则是“计算树”。 如果树中至少有一个分支导致接受状态，那么NTM就会接受这个输入状态。

  决策图如下：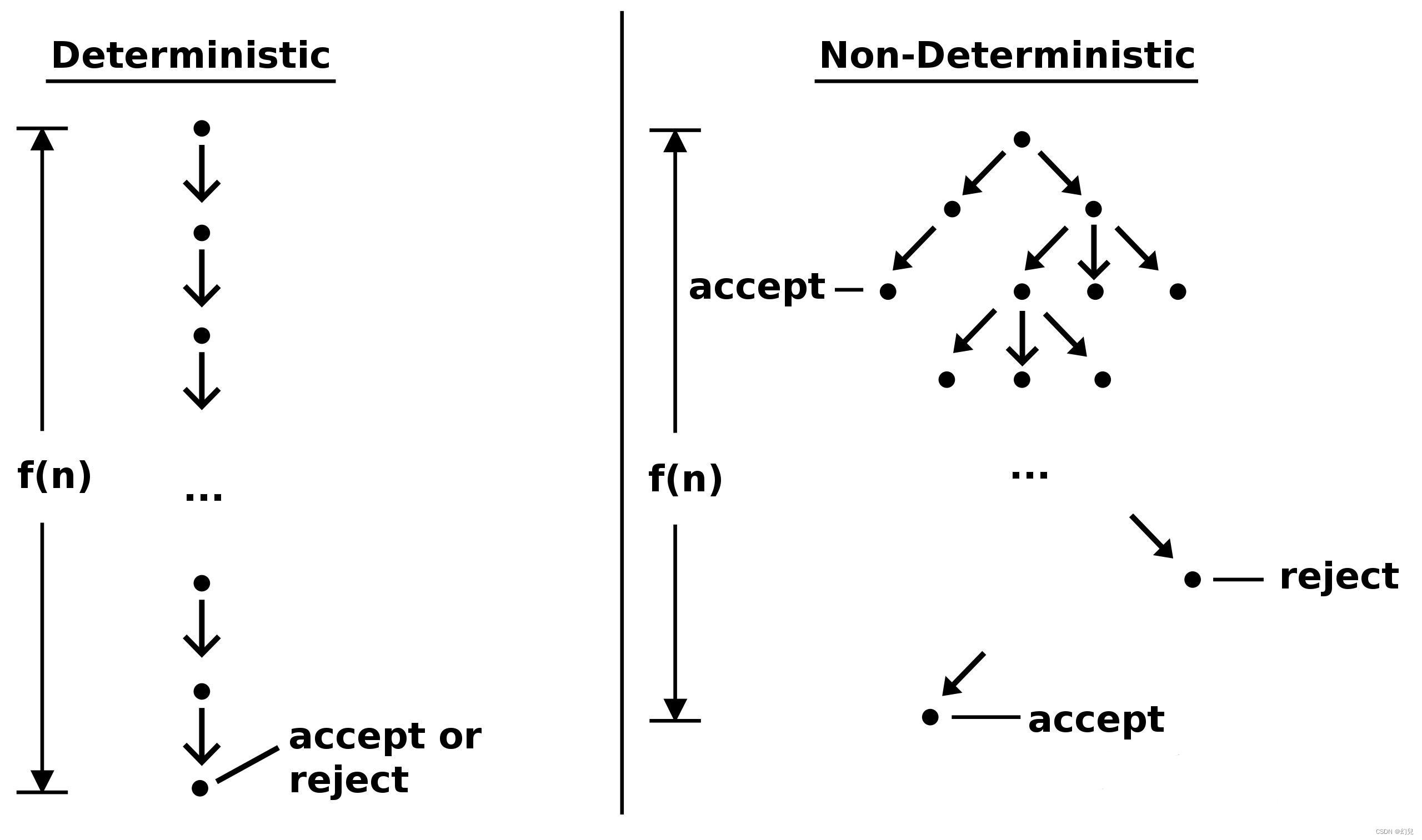

---

四、PageRank

1、基本信息

   基于词图模型的关键词提取算法： TextRank。
   来源：Google 创始人拉里·佩奇和谢尔盖·布林于 1997 年构建早期的搜索系统原型时提出的链接分析算法，通过计算网页链接的数量和质量来粗略估计网页的重要性。
   应用：该算法创立之初即应用在谷歌的搜索引擎中，是谷歌搜索的核心算法，对网页进行排名，从而解决互联网网页的价值排序问题

2、核心思想

   链接数量 ：如果一个网页被很多其他网页链接到，说明这个网页比较重要，也就是 PageRank 值会相对较高。
   链接质量 ：如果一个 PageRank 值很高的网页链接到一个其他的网页，那么被链接到的网页的 PageRank 值会相应地因此而提高。

3、基本原理

   可以将整个万维网看作一张有向图，网页构成了图中的节点。

   任务是从图中挖掘每个节点的权重作为其重要性的度量。
   一个节点如果由很多个其他节点指向它，那么这个节点应该就很重要。
   如果有多个高权重的节点指向某一节点，且这个节点指向外部的链接数很少，那么这个被链接的点显然非常重要。

4、算法流程

   对任意一个网页$P$，以$I(P)$表述其重要性，并称之为网页排序。
   网页$P_i$的重要性就是所有指向这个网页的其他网页所贡献的重要性的加和。那么就有：
$$I(P_i)=\sum _{P_j\in \ln (P_i)}\frac{I(P_j)}{|out(P_j)|}$$
  $I(P_i)$是网页$i$ 的重要性（PR 值）
  $\ln (P_i)$表示节点$P_i$的前驱节点集合
  $out(P_j)$ 表示节点$P_j$的后继节点集合
  $|out(P_j)|$是集合中元素的个数

  首先,需要确定指向它的其他网页的重要性，建立一个矩阵，称为超链矩阵(hyperlink matrix)，$H=[H_{ij}]$，其中第$i$行第$j$列的元素（代表了第$j$个网页分给第$i$个网页的重要性）为： H i j = { 0 ，其他情况 1 ∣ o u t ( P j ) ∣ ，如果 P j ∈ ln ⁡ ( P i ) {H_{ij}} =\{ _{0，其他情况}^{\frac{1}{{{\rm{|out(}}{{\rm{P}}_j}{\rm{)|}}}}，如果{P_j} \in \ln ({P_i})} Hij​={0，其他情况∣out(Pj​)∣1​，如果Pj​∈ln(Pi​)​
  注意到H有一些特殊的性质：
  1.它所有的元都是非负的
  2.除非对应这一列的网页没有任何链接，它的每一列的和为1
  所有元均非负且列和为1的矩阵称为随机矩阵，随机矩阵将在下述内容中起到重要作用。（矩阵中有一个元素满足随机分布时，这个矩阵就可称为随机矩阵）

  其次,我们还需要定义向量$I=[I(P_i)]$,它的元素为所有网页的网页排序——重要性的排序值。
  这样前面定义的网页排序还可以如下表示：$I=HI$
  即：向量$I$是矩阵$H$对应特征值1的特征向量。我们也称之为矩阵$H$的平稳向量(stationary vector)。

5、求超链接矩阵的平稳向量的方法——幂法

  幂法是一种计算矩阵主特征值（矩阵按模最大的特征值）及对应特征向量的迭代方法，特别是用于大型稀疏矩阵。
  首先选择$I$的备选向量$I_0$，进而按下式产生向量序列$I^k$
$$I^{k+1}=H{I}^k,k=0,1,2,...$$
  一般原理：序列$I^k$将收敛到平稳向量$I$

6、幂法实现的两大问题

（1）悬挂点问题

  考虑如下包含两个网页的小网络，其中一个链接到另一个：

  在这个例子中，两个网页的重要性排序值均为0，这样我们无法获知两个网页之间的相对重要性信息。问题在于网页P2没有任何链接。
  因此，在每个迭代步骤中，它从网页P1获取了一些重要性，但却没有赋给其他任何网页。这样将耗尽网络中的所有重要性。
  没有任何链接的网页称为悬挂点(dangling nodes)
  为了能够继续进行，我们需要随机选取下一个网页：也就是说，我们假定悬挂点可以链接到其他任何一个网页。
  相当于对超链接矩阵做修正：将其中所有元都为0的列替换为所有元均为$\frac{1}{n}$的列，修正后不存在悬挂点。
  即$S=H+A$
  矩阵A:对应于悬挂点的列的每个元均为$\frac{a}{n}$，其余元均为0
修正以后:

（2）重要性水槽

  蓝色方框部分，有链接进入，却没有链接转到外部，正如前述悬挂点的例子。其他网页的重要性被“排”到这个“重要性水槽”中。这种情形发生在矩阵S为可约时。
  为得到一个本原且不可约的矩阵，我们需要修正随机跳转网页的方式。
  本来的，随机跳转摸式完全由矩阵S决定。
  现在的，一部分可能遵循矩阵S的方式跳转，也可能随机选
择下一个页面。
  若记所有元均为1的$n\ast n$矩阵为$J$，那么我们就可以得到谷歌矩阵(Google matrix):$$G=\alpha S+(1-\alpha )\frac{1}{n}J$$

  需要选择一个概率$\alpha$，遵循矩阵$S$的方式跳转的概率为$\alpha$，而随机地选择下一个页面的概率是$1-\alpha$。并且根据前面推导，$\alpha$越接近1，则意味着网络原有的超链接结构在计算时的权重更大，更接近网页重要性信息。

  综合考虑，算法发明者选择其值：$\alpha$=0.85