题目链接
Solution
把题中 f ( l , r ) f(l,\ r) f(l, r) 的定义改为 f ( l − 1 , r ) f(l - 1, \ r) f(l−1, r),即令 f ( l , r ) : = f ( l − 1 , r ) f(l, \ r) := f(l - 1, \ r) f(l, r):=f(l−1, r),如下式所示,其中 s i = ∑ j = 1 i a j s_i = \sum\limits_{j = 1}^{i}{a_j} si=j=1∑iaj,表示 a i a_i ai 的前缀和
f ( l , r ) = ( s r − s l + r ( r + 1 ) 2 − l ( l + 1 ) 2 + k ) 2 f(l, \ r) = (s_r - s_l + \frac{r(r + 1)}{2} - \frac{l(l + 1)}{2} + k)^2 f(l, r)=(sr−sl+2r(r+1)−2l(l+1)+k)2
再令 v i = s i + i ( i + 1 ) 2 v_i = s_i + \frac{i(i + 1)}{2} vi=si+2i(i+1),化简得
f ( l , r ) = [ ( v r + k ) − v l ] 2 = ( v r + k ) 2 + v l 2 − 2 ( v r + k ) v l f(l,\ r) = [(v_r + k) - v_l]^2 = (v_r + k)^2 + v_l^2 - 2(v_r + k)v_l f(l, r)=[(vr+k)−vl]2=(vr+k)2+vl2−2(vr+k)vl
设 d p [ c ] [ i ] dp[c][i] dp[c][i] 表示将前 i i i 个数分为 c c c 段的最小值。
考虑其转移
d p [ c ] [ i ] = min 0 ⩽ j < i ( d p [ c − 1 ] [ j ] + f ( j , i ) ) = min 0 ⩽ j < i ( d p [ c − 1 ] [ j ] + ( v i + k ) 2 + v j 2 − 2 ( v i + k ) v j ) \begin{align*} dp[c][i] &= \min\limits_{0 \leqslant j < i}(dp[c - 1][j] + f(j, \ i)) \\ &= \min\limits_{0 \leqslant j < i}(dp[c - 1][j] + (v_i + k)^2 + v_j^2 - 2(v_i + k)v_j) \end{align*} dp[c][i]=0⩽j<imin(dp[c−1][j]+f(j, i))=0⩽j<imin(dp[c−1][j]+(vi+k)2+vj2−2(vi+k)vj)
根据斜率优化 D P DP DP,我们将纯变量放到左边称为 y y y,将带有“临时常量”系数的放到右边称为 x x x,最终得到(这里默认是依赖于上一维,所以省略 c c c 和 c − 1 c - 1 c−1)
d p [ j ] + v j 2 = 2 ( v i + k ) v j + [ d p i − ( v i + k ) 2 ] y = k x + b \begin{align*} dp[j] + v_j^2 &= 2(v_i + k)v_j + [dp_i - (v_i + k)^2] \\ y &= kx + b \end{align*} dp[j]+vj2y=2(vi+k)vj+[dpi−(vi+k)2]=kx+b
上式中,有如下对应关系
y = d p [ j ] + v j 2 k = 2 ( v i + k ) x = v j b = d p i − ( v i + k ) 2 \begin{align*} y &= dp[j] + v_j^2 \\ k &= 2(v_i + k) \\ x &= v_j \\ b &= dp_i - (v_i + k)^2 \end{align*} ykxb=dp[j]+vj2=2(vi+k)=vj=dpi−(vi+k)2
对于 y = k x + b y = kx + b y=kx+b 这条直线,我们最终要的就是截距 b b b 最小,而且这里随着 x x x 增加, y y y 严格增加,所以维护一个关于 ( x , y ) (x,\ y) (x, y) 点对的下凸包即可。
对于 d p [ i ] dp[i] dp[i],从下往上逼近凸包的直线斜率为 2 ( v i + k ) 2(v_i + k) 2(vi+k),当这条直线第一次碰到凸包上的点,截距就是最小的。
我们可以用单调队列维护这个凸包,即对于凸包最左侧的两个相邻点产生直线的斜率 k ′ k' k′,若 k ′ ⩽ 2 ( v i + k ) k' \leqslant 2(v_i + k) k′⩽2(vi+k),就将凸包最左侧的点弹出,这样能保证队头一定是最优的。
而要把第 i i i 个点插入队尾,就要求 i i i 与凸包最右侧的点产生的斜率 k 1 k_1 k1,严格大于凸包最右侧两点产生的斜率 k 2 k_2 k2(这是根据下凸包的定义来的),如下图所示(图片来源)
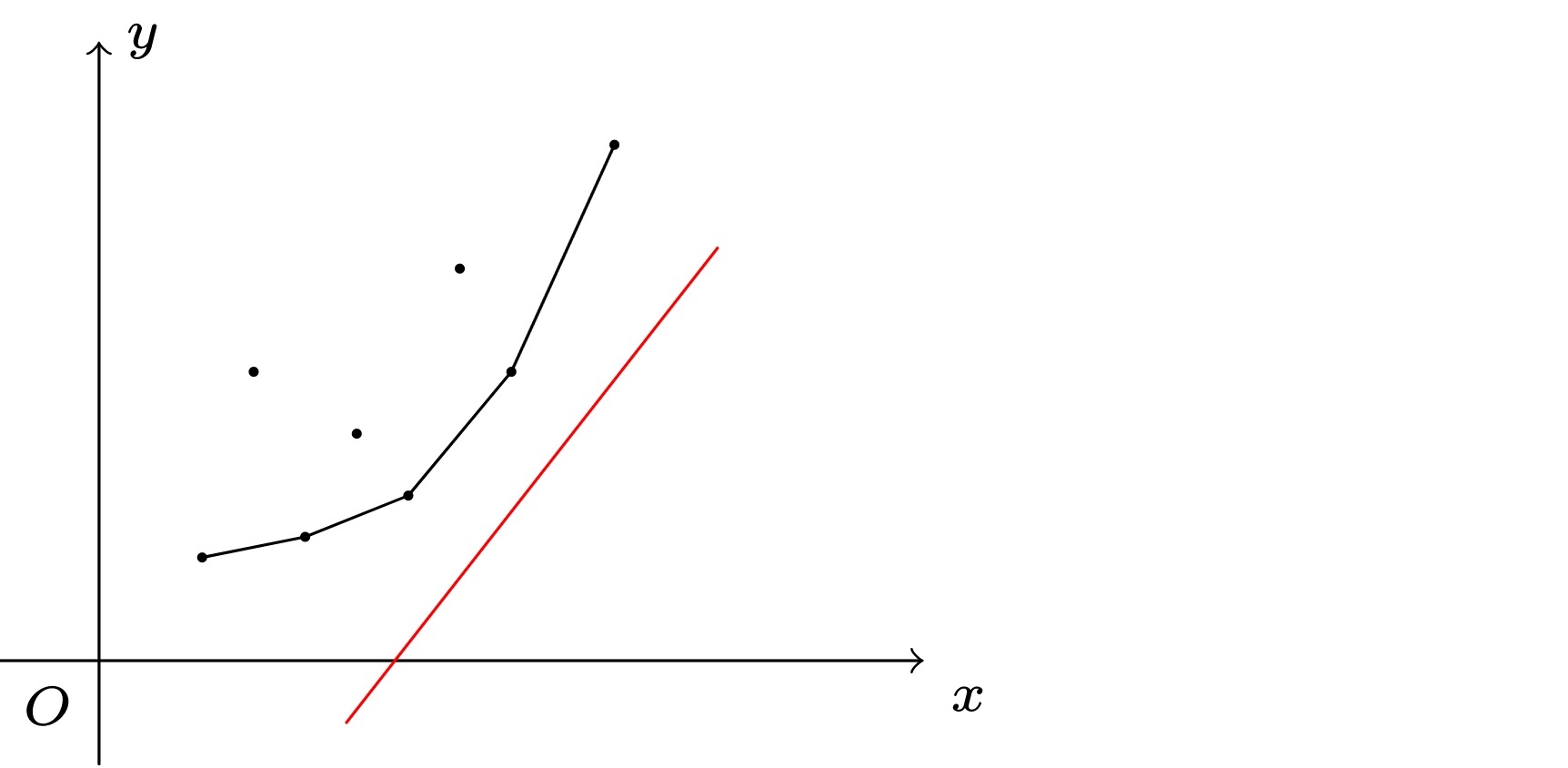
在这里,斜率 k ′ k' k′ 的计算公式为 y i − y j x i − x j \frac{y_i - y_j}{x_i - x_j} xi−xjyi−yj。
最后一点是,每次更新的时候, j j j 的范围其实是 [ c − 1 , i ) [c - 1, \ i) [c−1, i),因为少于 c − 1 c - 1 c−1 个数一定不可能被分为 c − 1 c - 1 c−1 段,这样可以节省一半计算量。
时间复杂度 O ( n 2 ) O(n^2) O(n2)。
C++ Code
#include <bits/stdc++.h>
using i64 = int64_t;
using u64 = uint64_t;
using f64 = double_t;
using i128 = __int128_t;
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cout << std::fixed << std::setprecision(12);
int n, m, k;
std::cin >> n >> m >> k;
std::vector<int> a(n);
for (int i = 0; i < n; i++) {
std::cin >> a[i];
}
std::vector<int> s(n + 1);
for (int i = 0; i < n; i++) {
s[i + 1] = s[i] + a[i];
}
std::vector<int> x(n + 1);
for (int i = 1; i <= n; i++) {
x[i] = s[i] + i * (i + 1) / 2;
}
std::vector<int> q(n + 1);
std::vector<i64> dp(n + 1), ndp(n + 1);
for (int i = 1; i <= n; i++) {
dp[i] = 1LL * (x[i] + k) * (x[i] + k);
}
std::vector<i64> y(n + 1);
for (int i = 1; i <= n; i++) {
y[i] = dp[i] + 1LL * x[i] * x[i];
}
for (int c = 2; c <= m; c++) {
int hh = 0, tt = 0;
q[tt++] = c - 1;
for (int i = c; i <= n; i++) {
int coef = x[i] + k;
while (hh + 1 < tt and (y[q[hh + 1]] - y[q[hh]]) <= (x[q[hh + 1]] - x[q[hh]]) * 2LL * coef) {
hh++;
}
int j = q[hh];
ndp[i] = dp[j] + 1LL * coef * coef + 1LL * x[j] * x[j] - 2LL * coef * x[j];
while (hh + 1 < tt and i128(y[i] - y[q[tt - 1]]) * (x[q[tt - 1]] - x[q[tt - 2]]) <= i128(y[q[tt - 1]] - y[q[tt - 2]]) * (x[i] - x[q[tt - 1]])) {
--tt;
}
q[tt++] = i;
}
for (int i = c; i <= n; i++) {
y[i] = ndp[i] + 1LL * x[i] * x[i];
}
dp.swap(ndp);
}
std::cout << dp[n] << "\n";
return 0;
}
























 835
835

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








