2101. 引爆最多的炸弹 Medium

给你一个炸弹列表。一个炸弹的 爆炸范围 定义为以炸弹为圆心的一个圆。

炸弹用一个下标从 0 开始的二维整数数组 bombs 表示，其中 bombs[i] = [xi, yi, ri] 。xi 和 yi 表示第 i 个炸弹的 X 和 Y 坐标，ri 表示爆炸范围的 半径 。

你需要选择引爆 一个 炸弹。当这个炸弹被引爆时，所有 在它爆炸范围内的炸弹都会被引爆，这些炸弹会进一步将它们爆炸范围内的其他炸弹引爆。

给你数组 bombs ，请你返回在引爆 一个 炸弹的前提下，最多 能引爆的炸弹数目。

示例 1：

输入：bombs = [[2,1,3],[6,1,4]]
输出：2
解释：
上图展示了 2 个炸弹的位置和爆炸范围。
如果我们引爆左边的炸弹，右边的炸弹不会被影响。
但如果我们引爆右边的炸弹，两个炸弹都会爆炸。
所以最多能引爆的炸弹数目是 max(1, 2) = 2 。

示例 2：

输入：bombs = [[1,1,5],[10,10,5]]
输出：1
解释：
引爆任意一个炸弹都不会引爆另一个炸弹。所以最多能引爆的炸弹数目为 1 。

示例 3：

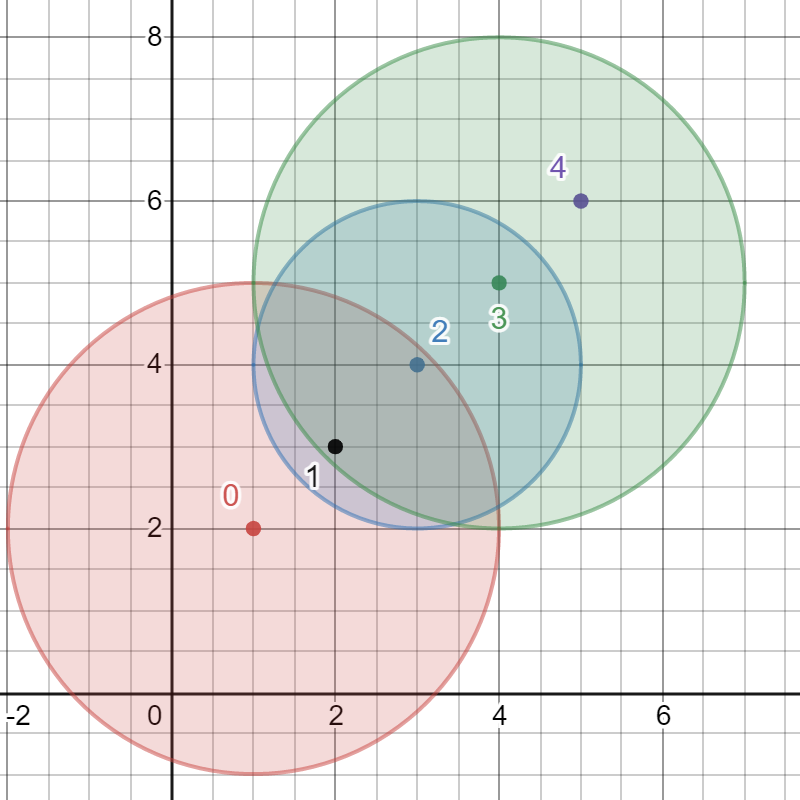
输入：bombs = [[1,2,3],[2,3,1],[3,4,2],[4,5,3],[5,6,4]]
输出：5
解释：
最佳引爆炸弹为炸弹 0 ，因为：
- 炸弹 0 引爆炸弹 1 和 2 。红色圆表示炸弹 0 的爆炸范围。
- 炸弹 2 引爆炸弹 3 。蓝色圆表示炸弹 2 的爆炸范围。
- 炸弹 3 引爆炸弹 4 。绿色圆表示炸弹 3 的爆炸范围。
所以总共有 5 个炸弹被引爆。

提示：

 ·1 <= bombs.length <= 100

 ·bombs[i].length == 3

 ·1 <= xi, yi, ri <= 105

题目大意：计算引爆一颗炸弹最多能引爆的炸弹数。

分析：

（1）本题可抽象为图的问题，若炸弹i能引爆炸弹j，则可视为炸弹i到炸弹j有一条有向边，因此可以抽象出一个有向图，则炸弹i可以引爆的炸弹数即为从结点i出发可到达的所有结点的总数（包括结点i）；

（2）由（1）可将题目转换为计算从某个结点出发能到达的结点的总数的最大值。设map[i]表示结点i可以到达的结点的集合，如果i可以到达k，则k能到达的结点i也能到达，因此i能到达的结点可以更新为map[i]=map[i]∪map[k]。由此可以用Floyd算法计算出各个结点可以到达的所有结点，最终的答案即为map数组中最大的集合中的结点个数；

（3）由于map[i]只需记录结点i是否可以到达其它结点，因此可以用bitset实现map[i]，则当i可以到达k时，map[i]|=map[k]。

class Solution {
public:
    int maximumDetonation(vector<vector<int>>& bombs) {
        int N=bombs.size();
        size_t ans=0;
        long long dis;
        vector<bitset<100>> map(N);
        for(int i=0,x1,y1,r1,x2,y2,r2;i<N;++i){
            x1=bombs[i][0];y1=bombs[i][1];r1=bombs[i][2];
            for(int j=i;j<N;++j){
                x2=bombs[j][0];y2=bombs[j][1];r2=bombs[j][2];
                dis=pow((x1-x2),2)+pow((y1-y2),2);
                if(dis<=(long long)r1*r1) map[i].set(j);
                if(dis<=(long long)r2*r2) map[j].set(i);
            }
        }
        for(int k=0;k<N;++k){
            for(int i=0;i<N;++i){
                //如果i可以到达k
                if(map[i].test(k)) map[i]|=map[k];
            }
        }
        for(const auto& bits:map) ans=max(ans,bits.count());
        return ans;
    }
};