this.parent = parent;
this.left = left;
this.right = right;
this.color = color;
this.key = key;
this.value = value;
}
public RBNode getParent() {
return parent;
}
public void setParent(RBNode parent) {
this.parent = parent;
}
public RBNode getLeft() {
return left;
}
public void setLeft(RBNode left) {
this.left = left;
}
public RBNode getRight() {
return right;
}
public void setRight(RBNode right) {
this.right = right;
}
public boolean isColor() {
return color;
}
public void setColor(boolean color) {
this.color = color;
}
public K getKey() {
return key;
}
public void setKey(K key) {
this.key = key;
}
public V getValue() {
return value;
}
public void setValue(V value) {
this.value = value;
}
}
}
复制代码
左旋代码实现
/**
* 围绕p左旋
* p pr(r)
* / | / \
* pl pr(r) => p rr
* / \ / \
* rl rr pl rl
*
* 左旋的时候
* p-pl 和 pr-rr的关系不变
* pr-rl 要变为 p-rl
* 也就是 rl要变为 p的右子节点
* 同时 p要成为 rl 的父节点
* 还有就是要判断 p 是否有父节点
* 如果没有
* r 变为 root 节点
* 如果有
* r.parent = p.parent
* 还要设置 r为 p.parent 的子节点(可能左也可能右)
* 如果 p.parent.left == p
* p.parent.left = r;
* 否则
* p.parent.right = r;
* 最后
* p.parent = r;
* r.left = p;
* @param p
*/
private void leftRotate(RBNode p){
if(p != null){
RBNode r = p.right;
// 1.设置 pr-rl 要变为 p-rl
// 把rl设置到p的右子节点
p.right = r.left;
if(r.left != null){
// 设置rl的父节点为p
r.left.parent = p;
}
// 2.判断p的父节点情况
r.parent = p.parent; // 不管 p是否有父节点,都把这个父节点设置为 r的父节点
if(p.parent == null){
root = r; // p没有父节点 则r为root节点
}else if(p.parent.left == p){
p.parent.left = r; // 如果p为 p.parent的左子节点 则 r 也为 p.parent的左子节点
}else{
p.parent.right = r; // 反之设置 r 为 p.parent的右子节点
}
// 最后 设置 p 为 r 的左子节点
r.left = p;
p.parent = r;
}
}
复制代码
右旋实现:
/**
* 围绕p右旋
* @param p
*/
public void rightRotate(RBNode p){
if(p != null){
RBNode r = p.left;
p.left = r.right;
if(r.right != null){
r.right.parent = p;
}
r.parent = p.parent;
if(p.parent == null){
root = r;
}else if(p.parent.left == p){
p.parent.left = r;
}else{
p.parent.right = r;
}
r.right = p;
p.parent = r;
}
}
复制代码
2 新增节点
------
2-3-4树中结点添加需要遵守以下规则:
* 插入都是向最下面一层插入
* 升元:将插入结点由 2-结点升级成 3-结点,或由 3-结点升级成 4-结点;
* 向 4-结点插入元素后,需要将中间元素提到父结点升元,原结点变成两个 2-结点,再把元素插入2-结点中,如果父结点也是 4-结点,则递归向上层升元,至到根结点后将树高加1;
而将这些规则对应到红黑树里,就是:
* 新插入的结点颜色为 红色 ,这样才可能不会对红黑树的高度产生影响。
* 2-结点对应红黑树中的单个黑色结点,插入时直接成功(对应 2-结点升元)。
* 3-结点对应红黑树中的 黑+红 子树,插入后将其修复成 红+黑+红 子树(对应 3-结点升元);
* 4-结点对应红黑树中的 红+黑+红 子树,插入后将其修复成 红色祖父+黑色父叔+红色孩子 子树,然后再把祖父结点当成新插入的红色结点递归向上层修复,直至修复成功或遇到 root 结点;
公式:**红黑树**+新增一个节点(红色)\*\*=\*\*对等的2-3-4树+新增一个节点
### 2.1 新增节点示例
我们通过新增2-3-4树的过程来映射对应的红黑树的节点新增
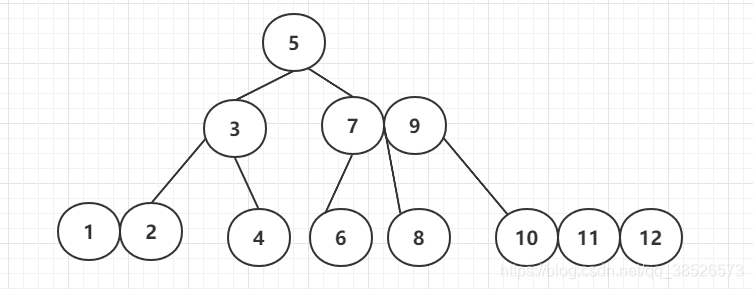
**2-3-4树的新增(全部在叶子节点完成)**
**1.新增一个节点,2 节点**
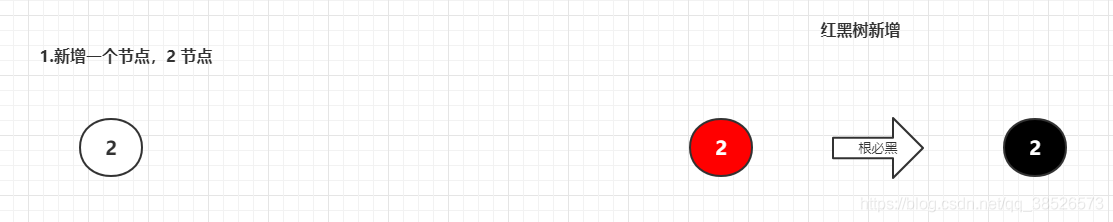
**2.新增一个节点,与2节点合并,直接合并**
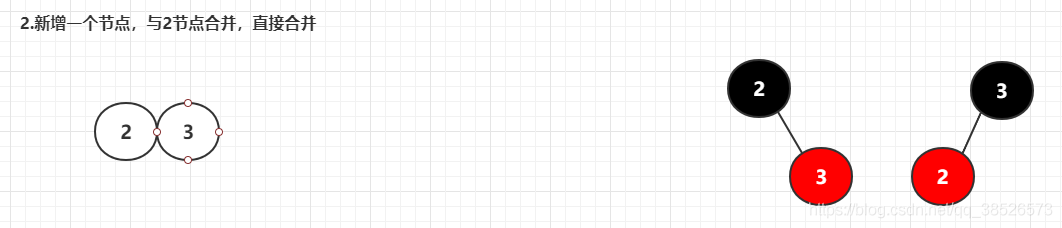
**3.新增一个节点,与3节点合并,直接合并**
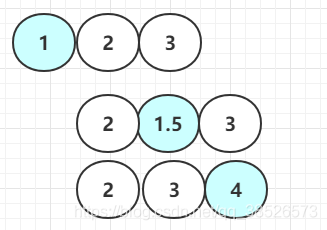
插入的值的位置会有3种情况
对应的红黑树为:
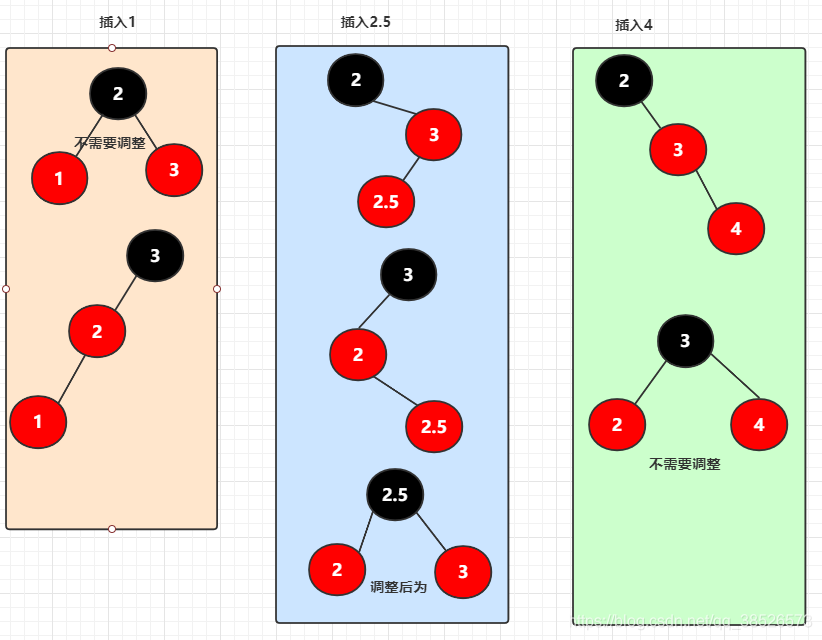
**4.新增一个节点,与4节点合并,此时需要分裂、**
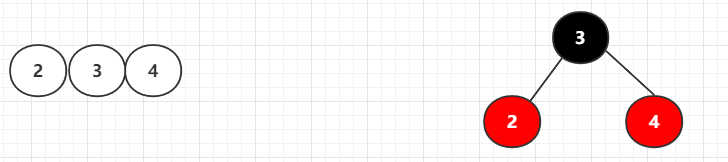
**插入值的位置可能是**
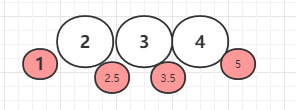
对应的红黑树的结构为
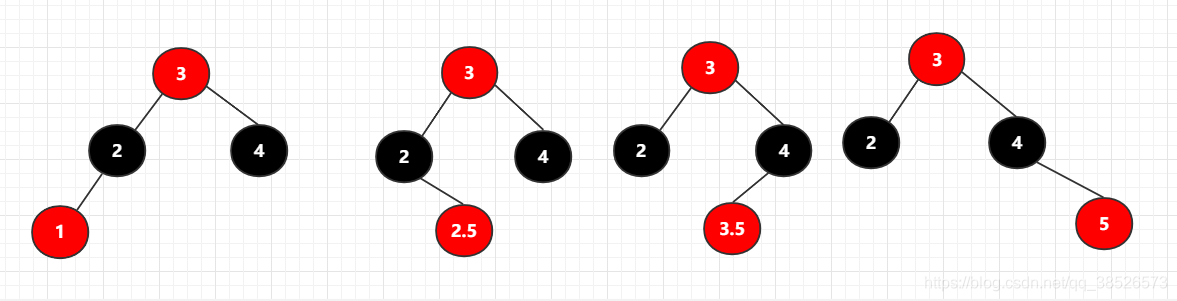
### 2.2 新增代码实现
红黑树的新增规则我们理清楚了,接下来就可以通过Java代码来具体的实现了。
先实现插入节点,这就是一个普通的二叉树的插入
/**
* 新增节点
* @param key
* @param value
*/
public void put(K key , V value){
RBNode t = this.root;
if(t == null){
// 说明之前没有元素,现在插入的元素是第一个
root = new RBNode<>(key , value == null ? key : value,null);
return ;
}
int cmp ;
// 寻找插入位置
// 定义一个双亲指针
RBNode parent;
if(key == null){
throw new NullPointerException();
}
// 沿着跟节点找插入位置
do{
parent = t;
cmp = key.compareTo((K)t.key);
if(cmp < 0){
// 左侧找
t = t.left;
}else if(cmp > 0){
// 右侧找
t = t.right;
}else{
// 插入节点的值==比较的节点。值替换
t.setValue(value==null?key:value);
return;
}
}while (t != null);
// 找到了插入的位置 parent指向 t 的父节点 t为null
// 创建要插入的节点
RBNode<K, Object> e = new RBNode<>(key, value == null ? key : value, parent);
// 然后判断要插入的位置 是 parent的 左侧还是右侧
if(cmp < 0){
parent.left = e;
}else{
parent.right = e;
}
// 调整 变色 旋转
fixAfterPut(e);
}
复制代码
然后再根据红黑树的特点来实现调整(旋转,变色)
private boolean colorOf(RBNode node){
return node == null ? BLACK:node.color;
}
private RBNode parentOf(RBNode node){
return node != null ? node.parent:null;
}
private RBNode leftOf(RBNode node){
return node != null ? node.left:null;
}
private RBNode rightOf(RBNode node){
return node != null ? node.right:null;
}
private void setColor(RBNode node ,boolean color){
if(node != null){
node.setColor(color);
}
}
/**
* 插入节点后的调整处理
* 1. 2-3-4树 新增元素 2节点添加一个元素将变为3节点 直接合并,节点中有两个元素
* 红黑树:新增一个红色节点,这个红色节点会添加在黑色节点下(2节点) --- 这种情况不需要调整
* 2. 2-3-4树 新增元素 3节点添加一个元素变为4节点合并 节点中有3个元素
* 这里有6中情况,( 根左左 根左右 根右右 根右左)这四种要调整 (左中右的两种)不需要调整
* 红黑树:新增红色节点 会添加到 上黑下红的节点中 = 排序后中间节点是黑色,两边节点是红色
*
* 3. 2-3-4树:新增一个元素 4节点添加一个元素需要裂变:中间元素升级为父节点,新增元素与剩下的其中一个合并
* 红黑树:新增节点是红色+爷爷节点是黑色,父亲节点和叔叔节点为红色 调整为
* 爷爷节点变红色,父亲和叔叔节点变为黑色,如果爷爷节点为root节点则调整为黑色
* @param x
*/
private void fixAfterPut(RBNode<K, Object> x) {
最后
我还通过一些渠道整理了一些大厂真实面试主要有:蚂蚁金服、拼多多、阿里云、百度、唯品会、携程、丰巢科技、乐信、软通动力、OPPO、银盛支付、中国平安等初,中级,高级Java面试题集合,附带超详细答案,希望能帮助到大家。

还有专门针对JVM、SPringBoot、SpringCloud、数据库、Linux、缓存、消息中间件、源码等相关面试题。

* 3. 2-3-4树:新增一个元素 4节点添加一个元素需要裂变:中间元素升级为父节点,新增元素与剩下的其中一个合并
* 红黑树:新增节点是红色+爷爷节点是黑色,父亲节点和叔叔节点为红色 调整为
* 爷爷节点变红色,父亲和叔叔节点变为黑色,如果爷爷节点为root节点则调整为黑色
* @param x
*/
private void fixAfterPut(RBNode<K, Object> x) {
最后
我还通过一些渠道整理了一些大厂真实面试主要有:蚂蚁金服、拼多多、阿里云、百度、唯品会、携程、丰巢科技、乐信、软通动力、OPPO、银盛支付、中国平安等初,中级,高级Java面试题集合,附带超详细答案,希望能帮助到大家。
[外链图片转存中…(img-DPPa7Fhk-1628093549088)]
还有专门针对JVM、SPringBoot、SpringCloud、数据库、Linux、缓存、消息中间件、源码等相关面试题。
[外链图片转存中…(img-2K8PcDGg-1628093549091)]






















 1696
1696

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








