基于微分 Vaiana Rosati 模型对 SDF 速率无关迟滞系统进行非线性时程分析的 Matlab 代码-CSDN博客

某大厂资深算法工程师，从事Matlab算法仿真工作10年,擅长智能优化算法、神经网络预测、机器学习、信号处理、元胞自动机、图像处理、路径规划、无人机、无线传感器网络、车间调度、生产调度等多种领域的Matlab仿真，更多仿真源码、算法改进、Matlab项目和期刊发表可私信合作。

本文链接：https://blog.csdn.net/m0_60703264/article/details/132493124

✅作者简介：热爱科研的Matlab仿真开发者，擅长数据处理、建模仿真、程序设计、完整代码获取、论文复现及科研仿真。

🍎个人主页：Matlab科研工作室

🍊个人信条：格物致知,完整Matlab代码及仿真咨询内容私信。

🌿 往期回顾可以关注主页，点击搜索

⛄ 内容介绍

非线性平衡方程

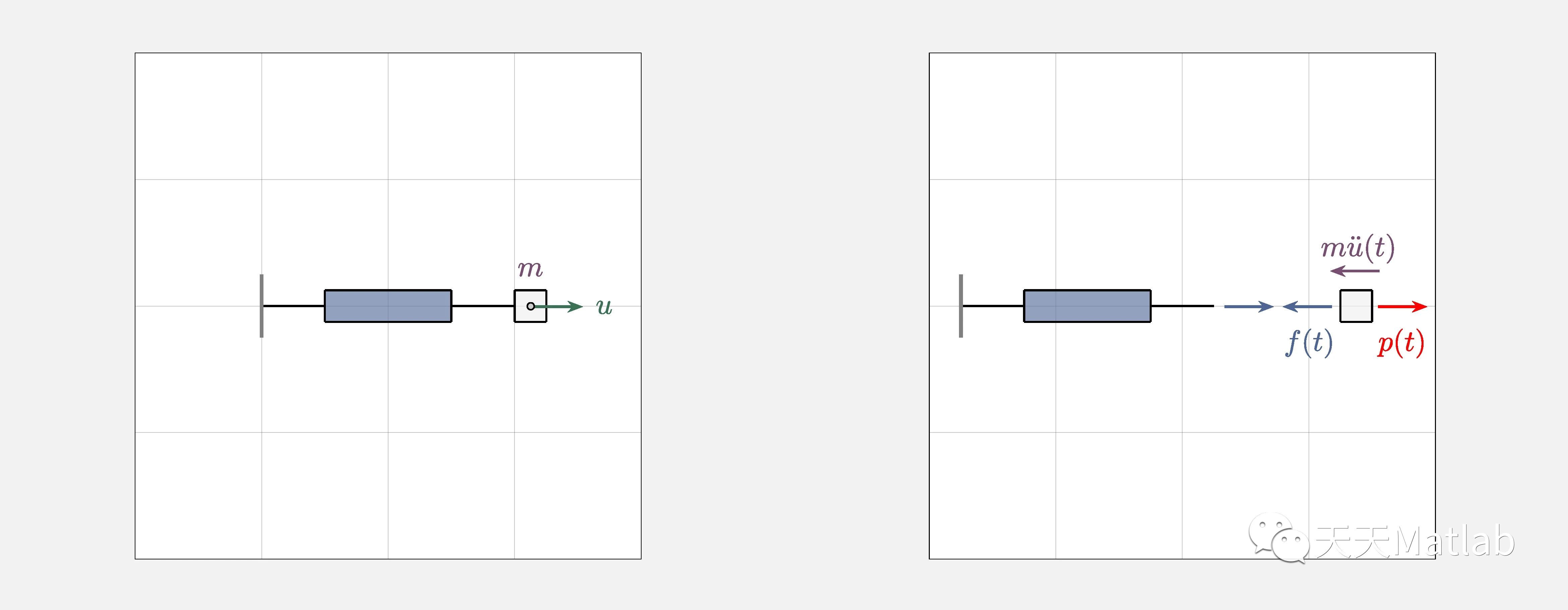
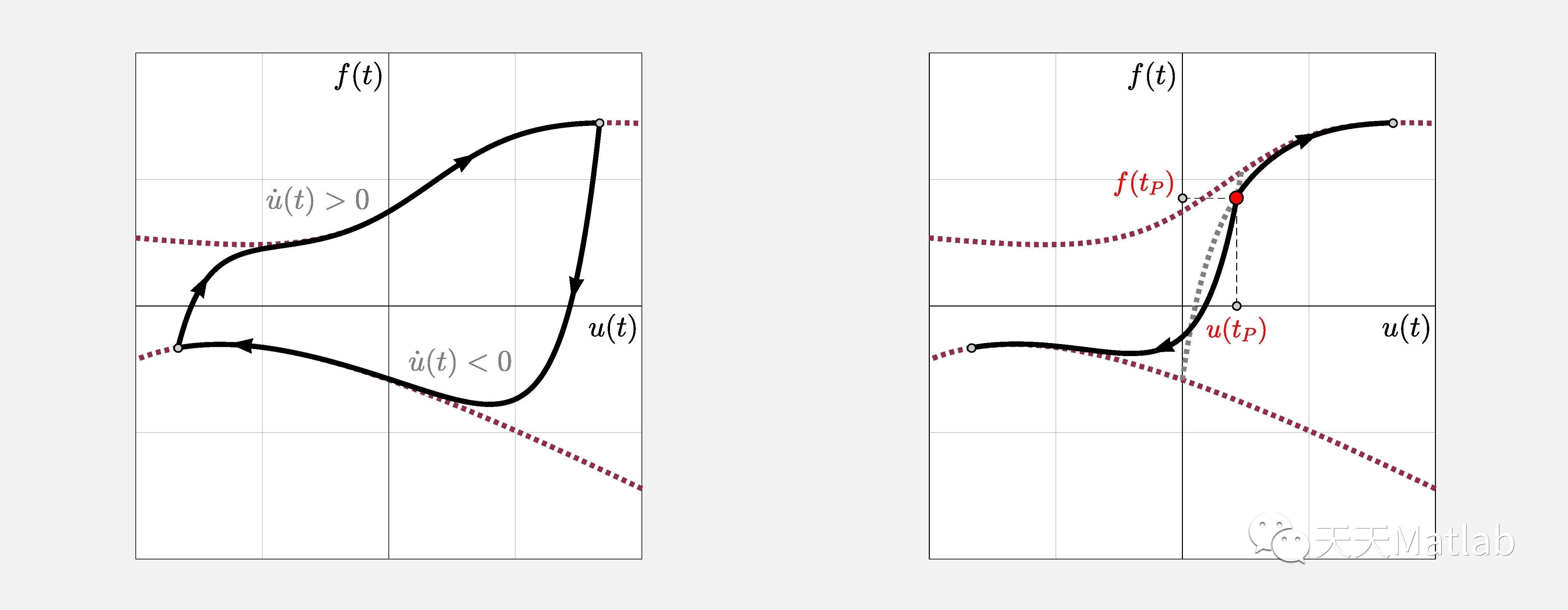
与速率无关的迟滞广义力

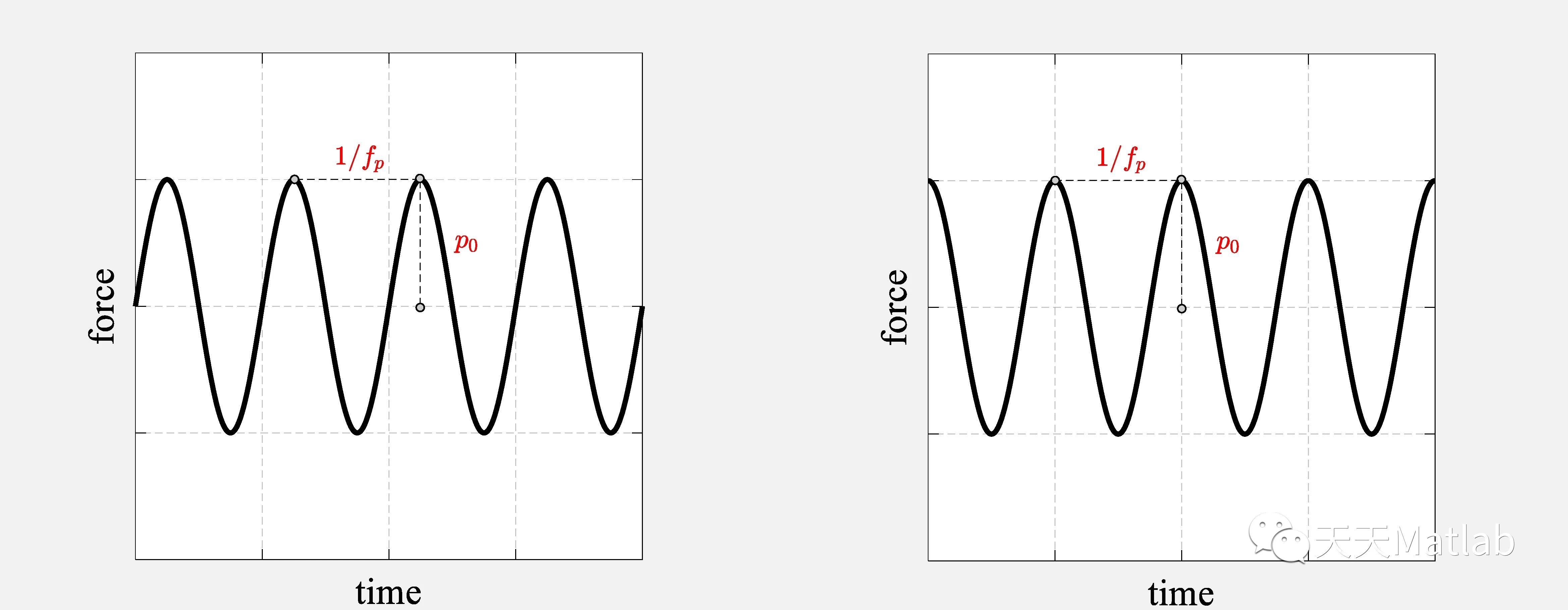
广义外力

数值法

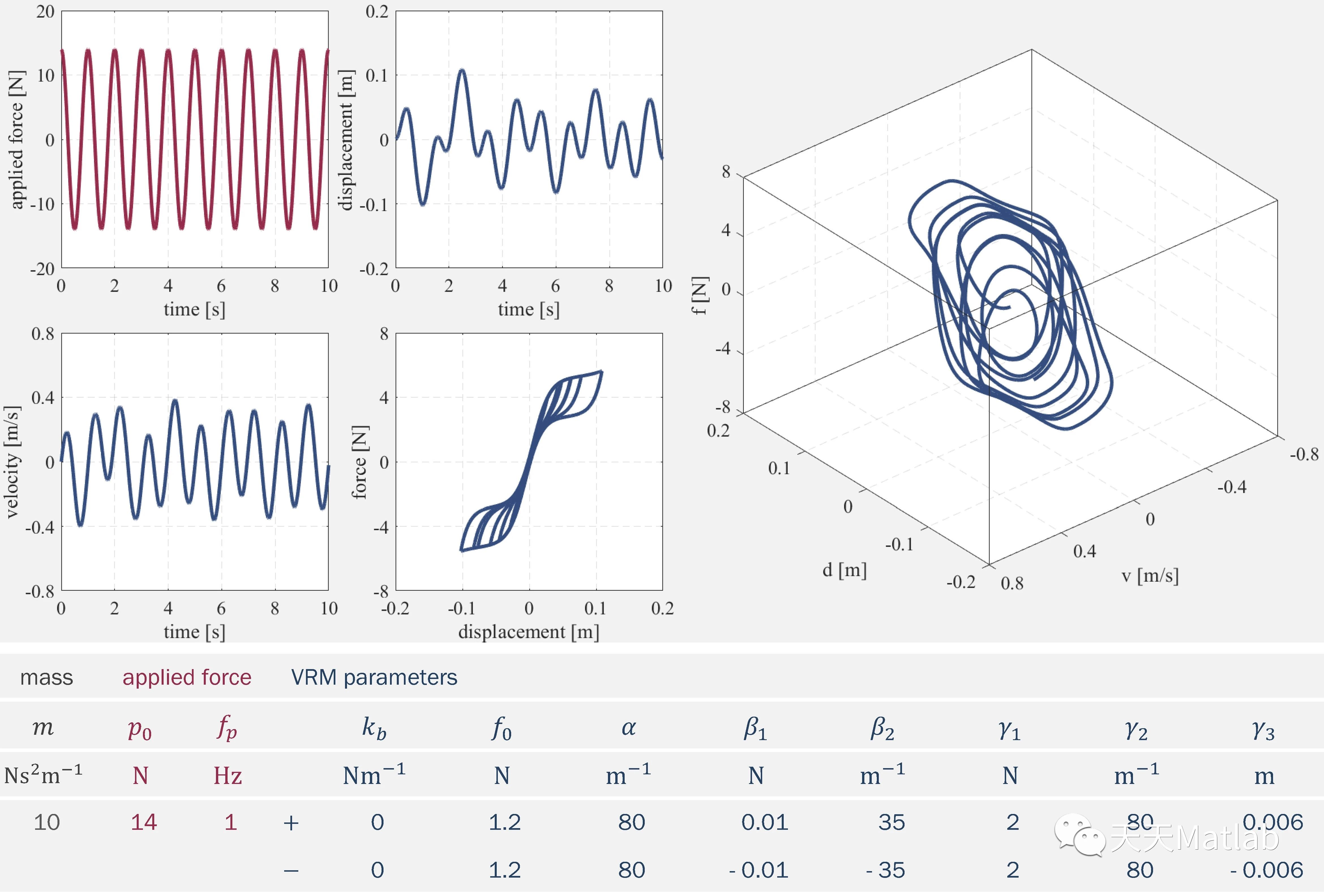
结果 - 正弦广义力

结果 – 余弦广义力

⛄ 核心代码

%  =========================================================================================clc; clear all; close all;%% SDF RATE-INDEPEDENT HYSTERETIC SYSTEM MASSm = 10;                                                                    % Ns^2/m%% VAIANA ROSATI MODEL PARAMETERSkbp     = 0;     kbm     = 0;                                              % N/mf0p     = 1.2;   f0m     = 1.2;                                            % Nalfap   = 80;    alfam   = 80;                                             % 1/mbeta1p  = 0.01;  beta1m  = -0.01;                                          % Nbeta2p  = 35;    beta2m  = -35;                                            % 1/mgamma1p = 2;     gamma1m = 2;                                              % Ngamma2p = 80;    gamma2m = 80;                                             % 1/mgamma3p = 0.006; gamma3m = -0.006;                                         % mparp    = [kbp f0p alfap beta1p beta2p gamma1p gamma2p gamma3p];           % -parm    = [kbm f0m alfam beta1m beta2m gamma1m gamma2m gamma3m];           % -%% EXTERNAL GENERALIZED FORCEtv = 0:0.001:10;                                                           % sfp = 1;                                                                    % Hzp0 = 14;                                                                   % Np  = p0*sin(2*pi*fp*tv(1:length(tv)));                                     % N%% RUNGE-KUTTA METHOD %% INITIAL SETTINGneq = 3;                                                                   % - number of equationsIC  = [0 0 0];                                                             % - initial conditions [x1 x2 x3]%% CALCULATIONS AT EACH TIME STEPoptions = odeset('RelTol',1e-10,'AbsTol',1e-10);[t,x]   = ode45(@(t,x) ODEs(t, x, neq, m, parp, parm, p, tv), tv, IC, options);%% PLOTSfigure('Color',[0.949019610881805 0.949019610881805 0.949019610881805]);subplot('Position',[0.05 0.58 0.2 0.4]);grid on; box on;xlabel('time [s]');ylabel('applied force [N]');axis([0 10 -20 20]);set(gca,'XTick',[0 2 4 6 8 10]);set(gca,'YTick',[-20 -10 0 10 20]);set(gca,'GridLineStyle','--');set(gca,'FontName','Times New Roman');set(gca,'FontSize',16);plot1 = line(t,p,'Color','[0.584313750267029 0.168627455830574 0.294117659330368]','LineWidth',3);subplot('Position',[0.30 0.58 0.2 0.4]);grid on; box on;xlabel('time [s]');ylabel('displacement [m]');axis([0 10 -0.2 0.2]);set(gca,'XTick',[0 2 4 6 8 10]);set(gca,'YTick',[-0.2 -0.1 0 0.1 0.2]);set(gca,'GridLineStyle','--');set(gca,'FontName','Times New Roman');set(gca,'FontSize',16);plot2 = line(t,x(:,1),'Color','[0.204, 0.302, 0.494]','LineWidth',3);subplot('Position',[0.05 0.08 0.2 0.4]);grid on; box on;xlabel('time [s]');ylabel('velocity [m/s]');axis([0 10 -0.8 0.8]);set(gca,'XTick',[0 2 4 6 8 10]);set(gca,'YTick',[-0.8 -0.4 0 0.4 0.8]);set(gca,'GridLineStyle','--');set(gca,'FontName','Times New Roman');set(gca,'FontSize',16);plot3 = line(t,x(:,2),'Color','[0.204, 0.302, 0.494]','LineWidth',3);subplot('Position',[0.30 0.08 0.2 0.4]);grid on; box on;xlabel('displacement [m]');ylabel('force [N]');axis([-0.2 0.2 -8 8]);set(gca,'XTick',[-0.2 -0.1 0 0.1 0.2]);set(gca,'YTick',[-8.0 -4.0 0 4.0 8.0]);set(gca,'GridLineStyle','--');set(gca,'FontName','Times New Roman');set(gca,'FontSize',16);plot4 = line(x(:,1),x(:,3),'Color','[0.204, 0.302, 0.494]','LineWidth',3);subplot('Position',[0.56 0.12 0.4 0.8]);grid on; box on;xlabel('d [m]');ylabel('v [m/s]');zlabel('f [N]');axis([-0.2 0.2 -0.8 0.8 -8 8]);set(gca,'XTick',[-0.2 -0.1 0 0.1 0.2]);set(gca,'YTick',[-0.8 -0.4 0 0.4 0.8]);set(gca,'ZTick',[-8.0 -4.0 0 4.0 8.0]);set(gca,'GridLineStyle','--');set(gca,'FontName','Times New Roman');set(gca,'FontSize',16);set(gca,'BoxStyle','full');view([229.572533907569 40.0908387200157]);plot5 = line(x(:,1),x(:,2),x(:,3),'Color','[0.204, 0.302, 0.494]','Linewidth',3);

⛄ 运行结果

⛄ 参考文献

Vaiana, Nicolò, and Luciano Rosati. “Classification and Unified Phenomenological Modeling of Complex Uniaxial Rate-Independent Hysteretic Responses.” Mechanical Systems and Signal Processing, vol. 182, Elsevier BV, Jan. 2023, p. 109539, doi:10.1016/j.ymssp.2022.109539.

Vaiana, Nicolò, and Luciano Rosati. “Analytical and Differential Reformulations of the Vaiana–Rosati Model for Complex Rate-Independent Mechanical Hysteresis Phenomena.” Mechanical Systems and Signal Processing, vol. 199, Elsevier BV, Sept. 2023, p. 110448, doi:10.1016/j.ymssp.2023.110448.