✅作者简介:热爱科研的Matlab仿真开发者,擅长数据处理、建模仿真、程序设计、完整代码获取、论文复现及科研仿真。
🍎个人主页:Matlab科研工作室
🍊个人信条:格物致知,完整Matlab代码及仿真咨询内容私信。
🌿 往期回顾可以关注主页,点击搜索
🔥 内容介绍
在通信系统中,大规模 MIMO 技术已经成为了一个热门话题。大规模 MIMO 技术能够利用多个天线来传输和接收信号,从而提高了信号的可靠性和传输速度。然而,由于信号传输的复杂性,大规模 MIMO 技术也面临着一些挑战。其中一个挑战就是如何在大规模 MIMO 系统中进行检测。为了解决这个问题,近似消息传递(AMP)技术被提出,并被广泛应用于大规模 MIMO 系统中。
AMP 技术是一种基于概率推断的算法,它能够在大规模 MIMO 系统中高效地进行检测。AMP 技术的核心思想是将复杂的检测问题转化为简单的推断问题。在 AMP 技术中,每个接收天线都会生成一个消息,这个消息包含了接收到的信号和噪声的统计信息。这些消息会被传递到下一个节点,然后根据这些消息进行推断和计算。最终,AMP 技术能够得出准确的检测结果。
AMP 技术在大规模 MIMO 系统中的应用已经被证明是非常有效的。它能够在高速移动的环境下实现高速数据传输,并且能够在复杂的干扰环境下实现可靠的信号检测。此外,AMP 技术还能够在低功耗的设备上实现高效的检测,这对于物联网应用非常重要。
虽然 AMP 技术在大规模 MIMO 系统中的应用非常成功,但是它也存在一些局限性。例如,AMP 技术需要大量的计算资源来进行推断和计算,这可能会导致系统的延迟增加。此外,AMP 技术对于信号的噪声和非线性特性比较敏感,这可能会影响检测的准确性。
总之,近似消息传递(AMP)技术是一种非常有效的大规模 MIMO 检测技术。它能够在复杂的环境下实现高效的信号检测,并且能够在低功耗的设备上实现高效的检测。虽然 AMP 技术存在一些局限性,但是它的优点远远超过了缺点。因此,AMP 技术有望成为未来大规模 MIMO 系统中最常用的检测技术之一。
📣 部分代码
function [MinCost, Hamming,Best] = BBO(ProblemFunction, DisplayFlag, ProbFlag, RandSeed)
% Biogeography-based optimization (BBO) software for minimizing a general function
% INPUTS: ProblemFunction is the handle of the function that returns
% the handles of the initialization, cost, and feasibility functions.
% DisplayFlag = true or false, whether or not to display and plot results.
% ProbFlag = true or false, whether or not to use probabilities to update emigration rates.
% RandSeed = random number seed
% OUTPUTS: MinCost = array of best solution, one element for each generation
% Hamming = final Hamming distance between solutions
% CAVEAT: The "ClearDups" function that is called below replaces duplicates with randomly-generated
% individuals, but it does not then recalculate the cost of the replaced individuals.
if ~exist('DisplayFlag', 'var')
DisplayFlag = true;
end
if ~exist('ProbFlag', 'var')
ProbFlag = false;
end
if ~exist('RandSeed', 'var')
RandSeed = round(sum(100*clock));
end
[OPTIONS, MinCost, AvgCost, InitFunction, CostFunction, FeasibleFunction, ...
MaxParValue, MinParValue, Population] = Init(DisplayFlag, ProblemFunction, RandSeed);
Population = CostFunction(OPTIONS, Population);
OPTIONS.pmodify = 1; % habitat modification probability
OPTIONS.pmutate = 0.005; % initial mutation probability
Keep = 2; % elitism parameter: how many of the best habitats to keep from one generation to the next
lambdaLower = 0.0; % lower bound for immigration probabilty per gene
lambdaUpper = 1; % upper bound for immigration probabilty per gene
dt = 1; % step size used for numerical integration of probabilities
I = 1; % max immigration rate for each island
E = 1; % max emigration rate, for each island
P = OPTIONS.popsize; % max species count, for each island
% Initialize the species count probability of each habitat
% Later we might want to initialize probabilities based on cost
for j = 1 : length(Population)
Prob(j) = 1 / length(Population);
end
% Begin the optimization loop
for GenIndex = 1 : OPTIONS.Maxgen
% Save the best habitats in a temporary array.
for j = 1 : Keep
chromKeep(j,:) = Population(j).chrom;
costKeep(j) = Population(j).cost;
end
% Map cost values to species counts.
[Population] = GetSpeciesCounts(Population, P);
% Compute immigration rate and emigration rate for each species count.
% lambda(i) is the immigration rate for habitat i.
% mu(i) is the emigration rate for habitat i.
[lambda, mu] = GetLambdaMu(Population, I, E, P);
if ProbFlag
% Compute the time derivative of Prob(i) for each habitat i.
for j = 1 : length(Population)
% Compute lambda for one less than the species count of habitat i.
lambdaMinus = I * (1 - (Population(j).SpeciesCount - 1) / P);
% Compute mu for one more than the species count of habitat i.
muPlus = E * (Population(j).SpeciesCount + 1) / P;
% Compute Prob for one less than and one more than the species count of habitat i.
% Note that species counts are arranged in an order opposite to that presented in
% MacArthur and Wilson's book - that is, the most fit
% habitat has index 1, which has the highest species count.
if j < length(Population)
ProbMinus = Prob(j+1);
else
ProbMinus = 0;
end
if j > 1
ProbPlus = Prob(j-1);
else
ProbPlus = 0;
end
ProbDot(j) = -(lambda(j) + mu(j)) * Prob(j) + lambdaMinus * ProbMinus + muPlus * ProbPlus;
end
% Compute the new probabilities for each species count.
Prob = Prob + ProbDot * dt;
Prob = max(Prob, 0);
Prob = Prob / sum(Prob);
end
% Now use lambda and mu to decide how much information to share between habitats.
lambdaMin = min(lambda);
lambdaMax = max(lambda);
for k = 1 : length(Population)
if rand > OPTIONS.pmodify
continue;
end
% Normalize the immigration rate.
lambdaScale = lambdaLower + (lambdaUpper - lambdaLower) * (lambda(k) - lambdaMin) / (lambdaMax - lambdaMin);
% Probabilistically input new information into habitat i
for j = 1 : OPTIONS.numVar
if rand < lambdaScale
% Pick a habitat from which to obtain a feature
RandomNum = rand * sum(mu);
Select = mu(1);
SelectIndex = 1;
while (RandomNum > Select) & (SelectIndex < OPTIONS.popsize)
SelectIndex = SelectIndex + 1;
Select = Select + mu(SelectIndex);
end
Island(k,j) = Population(SelectIndex).chrom(j);
else
Island(k,j) = Population(k).chrom(j);
end
end
end
if ProbFlag
% Mutation
Pmax = max(Prob);
MutationRate = OPTIONS.pmutate * (1 - Prob / Pmax);
% Mutate only the worst half of the solutions
Population = PopSort(Population);
for k = round(length(Population)/2) : length(Population)
for parnum = 1 : OPTIONS.numVar
if MutationRate(k) > rand
Island(k,parnum) = floor(MinParValue + (MaxParValue - MinParValue + 1) * rand);
end
end
end
end
% Replace the habitats with their new versions.
for k = 1 : length(Population)
Population(k).chrom = Island(k,:);
end
% Make sure each individual is legal.
Population = FeasibleFunction(OPTIONS, Population);
% Calculate cost
Population = CostFunction(OPTIONS, Population);
% Sort from best to worst
Population = PopSort(Population);
% Replace the worst with the previous generation's elites.
n = length(Population);
for k = 1 : Keep
Population(n-k+1).chrom = chromKeep(k,:);
Population(n-k+1).cost = costKeep(k);
end
% Make sure the population does not have duplicates.
Population = ClearDups(Population, MaxParValue, MinParValue);
% Sort from best to worst
Population = PopSort(Population);
% Compute the average cost
[AverageCost, nLegal] = ComputeAveCost(Population);
% Display info to screen
MinCost = [MinCost Population(1).cost];
AvgCost = [AvgCost AverageCost];
if DisplayFlag
disp(['The best and mean of Generation # ', num2str(GenIndex), ' are ',...
num2str(MinCost(end)), ' and ', num2str(AvgCost(end))]);
end
end
Best=Conclude(DisplayFlag, OPTIONS, Population, nLegal, MinCost);
% Obtain a measure of population diversity
% for k = 1 : length(Population)
% Chrom = Population(k).chrom;
% for j = MinParValue : MaxParValue
% indices = find(Chrom == j);
% CountArr(k,j) = length(indices); % array containing gene counts of each habitat
% end
% end
Hamming = 0;
% for m = 1 : length(Population)
% for j = m+1 : length(Population)
% for k = MinParValue : MaxParValue
% Hamming = Hamming + abs(CountArr(m,k) - CountArr(j,k));
% end
% end
% end
if DisplayFlag
disp(['Diversity measure = ', num2str(Hamming)]);
end
return;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function [Population] = GetSpeciesCounts(Population, P)
% Map cost values to species counts.
% This loop assumes the population is already sorted from most fit to least fit.
for i = 1 : length(Population)
if Population(i).cost < inf
Population(i).SpeciesCount = P - i;
else
Population(i).SpeciesCount = 0;
end
end
return;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function [lambda, mu] = GetLambdaMu(Population, I, E, P)
% Compute immigration rate and extinction rate for each species count.
% lambda(i) is the immigration rate for individual i.
% mu(i) is the extinction rate for individual i.
for i = 1 : length(Population)
lambda(i) = I * (1 - Population(i).SpeciesCount / P);
mu(i) = E * Population(i).SpeciesCount / P;
end
return;⛳️ 运行结果
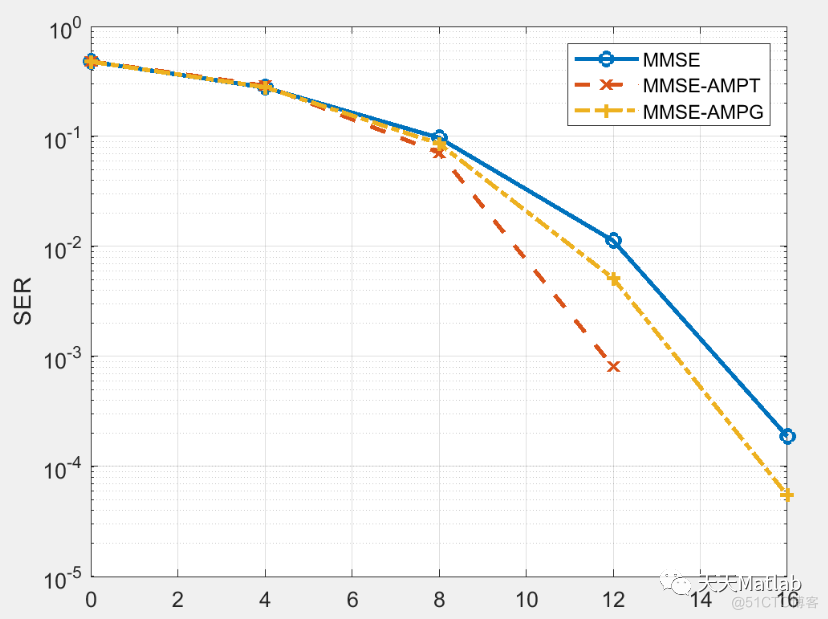

🔗 参考文献
[1] 卞海红,徐国政,王新迪.一种基于PSO和双向GRU的短期负荷预测模型:CN202111215326.2[P].CN202111215326.2[2023-09-18].
[2] 马莉,潘少波,代新冠,等.基于PSO-Adam-GRU的煤矿瓦斯浓度预测模型[J].西安科技大学学报, 2020, 40(2):6.DOI:CNKI:SUN:XKXB.0.2020-02-024.

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










