✅作者简介:热爱数据处理、建模、算法设计的Matlab仿真开发者。
🍎更多Matlab代码及仿真咨询内容点击 🔗:Matlab科研工作室
🍊个人信条:格物致知。
🔥 内容介绍
在无线通信系统中,传输过程中会受到各种干扰,其中大气湍流、混沌和相位噪声是常见的干扰源。这些干扰会导致误码率的增加,从而降低系统的可靠性和性能。因此,对于这些干扰的建模和仿真分析是非常重要的。
本文将介绍一种基于matlab的BPSK(二进制相移键控)误码算法流程,该算法能够计算在加入大气湍流、混沌和相位噪声情况下的误码率。通过这种算法,我们可以评估系统在不同干扰条件下的性能,并且可以优化系统参数以提高系统的可靠性。
首先,我们需要了解BPSK调制和解调的基本原理。BPSK是一种常用的二进制调制方式,其中0和1分别用正弦波的两个相位表示。在发送端,将二进制数据转换为BPSK信号,然后通过信道传输到接收端。在接收端,通过解调将BPSK信号转换回二进制数据。
然而,在传输过程中,信号会受到各种干扰的影响。大气湍流是由于大气层中的湍流运动引起的,会导致信号的强度和相位发生变化。混沌干扰是由于非线性系统的混沌特性引起的,会导致信号的频率和相位发生随机变化。相位噪声是由于各种原因引起的信号相位的随机变化。
为了计算在这些干扰情况下的误码率,我们需要进行一系列的仿真实验。首先,我们需要生成BPSK信号,并将其加入大气湍流、混沌和相位噪声。然后,我们使用解调算法将接收到的信号转换为二进制数据,并与原始数据进行比较,计算误码率。
在matlab中,我们可以使用信号处理工具箱和通信工具箱来实现这个算法。首先,我们可以使用信号处理工具箱中的函数生成BPSK信号。然后,我们可以使用通信工具箱中的函数模拟大气湍流、混沌和相位噪声,并将其叠加到BPSK信号中。最后,我们可以使用通信工具箱中的解调函数将接收到的信号转换为二进制数据,并计算误码率。
通过对不同干扰条件下的误码率进行仿真实验,我们可以评估系统的性能,并优化系统参数以提高系统的可靠性。例如,我们可以通过增加信号的功率或使用更复杂的解调算法来降低误码率。此外,我们还可以通过改变大气湍流和混沌的参数来研究它们对系统性能的影响。
总之,本文介绍了一种基于matlab的BPSK误码算法流程,该算法能够计算在加入大气湍流、混沌和相位噪声情况下的误码率。通过这种算法,我们可以评估系统在不同干扰条件下的性能,并且可以优化系统参数以提高系统的可靠性。这对于无线通信系统的设计和优化非常重要。
📣 部分代码
%---------------------------------基本信息---------------------------------%
%
% 实现功能:计算加入大气、混沌、相位噪声情况下的BPSK误码率
%
%-------------------------------------------------------------------------%
%-------------------------------版本说明-------------------------------%
%{
1.在V2版本的基础上加入混沌噪声的BER
2.分析了4种激光器的线宽,分别为500 800 1200 2000KHz
3.在V3版本的基础上加入 强湍流 弱湍流 还有夜视情况下的大气湍流 PDF 两重积分 单独一重pdf不等于0
4.在V4版本的基础上加入重新整理的公式部分
5.具体版本说明的word 下载网址:
%}
%-------------------------------版本问题-------------------------------%
%{
1.beta的取值问题,
%-------------------------------BPSK解调模块相关参数-------------------------------%
%-------------------------------失配噪声参数-------------------------------%
%beta=10; %chaos feedback gain 环路增益
%-------------------------------探测器参数-------------------------------%
%%平衡探测器参数
yita=0.8; %η量子效率
R_d=yita*e/(hp*v); %计算PD响应度R_d
% 探测器噪声参数设置
G=1; %探测器增益
F_A=G^0.5;
I_d=10^-9; %暗电流
delt_F=2*10^9; %噪声等效带宽
Ts=1/delt_F; %噪声等效时宽
T=300; %探测器温度
R_L=50; %探测器负载电阻
k_B=1.380649*10^-23; %波尔兹曼常数
F_n=1; %探测器噪声因子⛳️ 运行结果
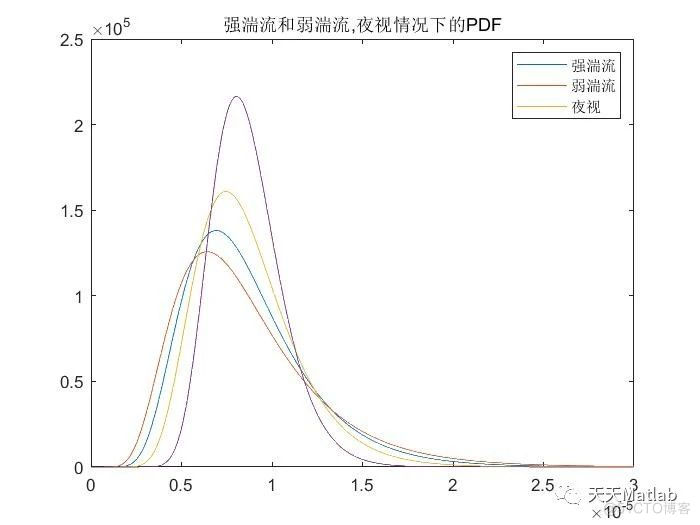
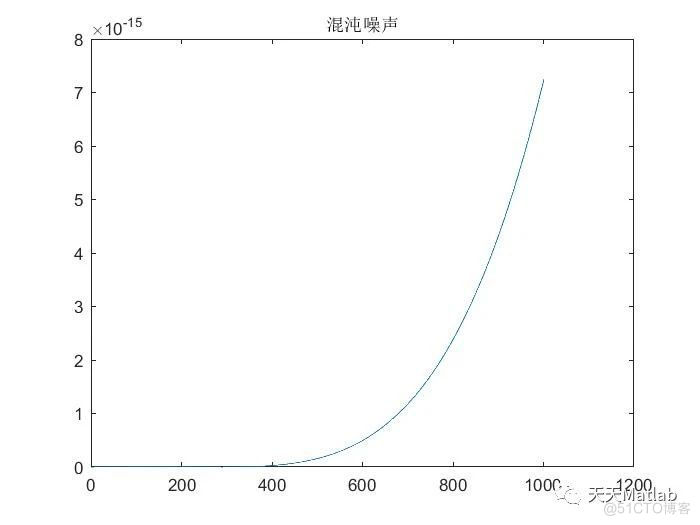
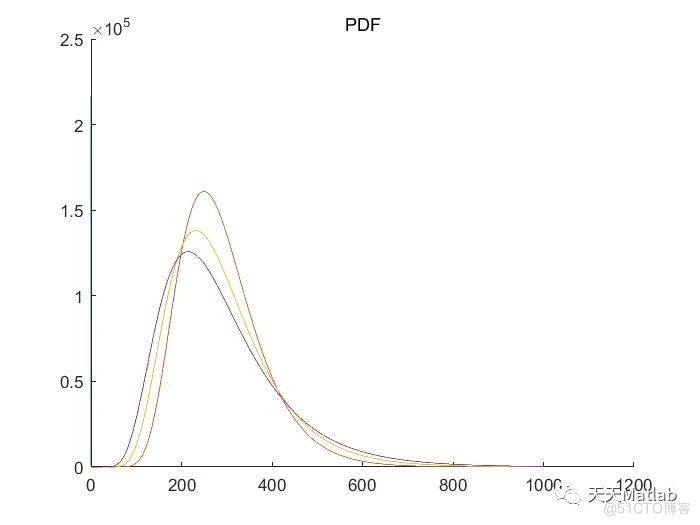
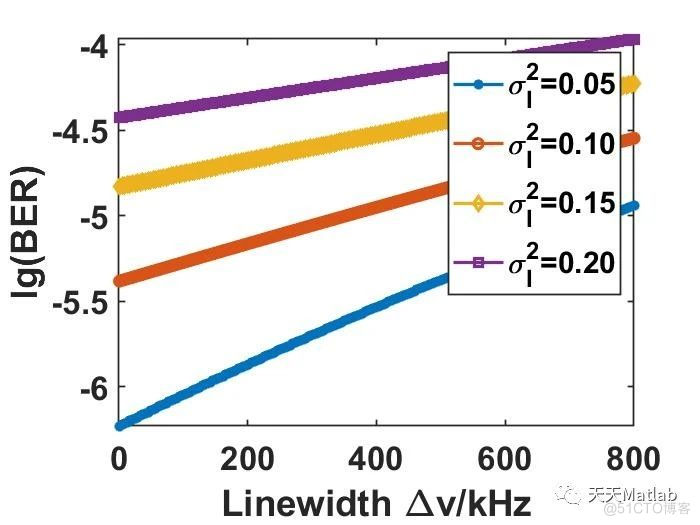
🔗 参考文献
[1] 徐光勇.大气湍流中的激光传输数值模拟及其影响分析[D].电子科技大学,2008.DOI:10.7666/d.D309974.
[2] 刘保菊,张长森.大气湍流对复杂路径下光强起伏及误码率的影响[J].应用科技, 2007, 34(3):4.DOI:10.3969/j.issn.1009-671X.2007.03.001.

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










