✅作者简介:热爱数据处理、建模、算法设计的Matlab仿真开发者。
🍎更多Matlab代码及仿真咨询内容点击 🔗:Matlab科研工作室
🍊个人信条:格物致知。
🔥 内容介绍
无人机技术的发展已经成为当今世界的热点话题之一。无人机编队技术作为无人机领域的重要研究方向之一,对于提高无人机的协同作战能力和应用价值具有重要意义。在无人机编队技术中,队形的实时切换是一个关键问题,而基于匈牙利算法实现无人机编队队形的实时切换成为了研究的热点之一。
匈牙利算法是一种用于解决指派问题的算法,它可以高效地找到最优的指派方案。在无人机编队中,队形的切换可以看作是一个指派问题,即将每架无人机指派到新的位置,使得整个编队的队形达到最优。因此,利用匈牙利算法来实现无人机编队队形的实时切换具有很大的潜力。
基于匈牙利算法实现无人机编队队形实时切换的关键在于如何构建指派问题的成本矩阵。成本矩阵的每个元素表示将某架无人机指派到某个位置的成本,而这个成本可以根据编队的要求来确定。一般来说,成本可以包括无人机之间的距离、速度、方向等因素。通过合理地构建成本矩阵,可以将队形的实时切换问题转化为一个指派问题,从而利用匈牙利算法来解决。
除了构建成本矩阵,基于匈牙利算法实现无人机编队队形实时切换还需要考虑到实时性和稳定性。在实际应用中,无人机编队往往需要在动态环境中进行任务执行,因此队形的实时切换需要在较短的时间内完成,并且要保持编队的稳定性,避免发生碰撞或混乱。因此,如何在保证实时性的同时保持稳定性成为了一个挑战。
针对这一挑战,研究人员提出了一些解决方案。例如,可以将匈牙利算法与预测控制方法相结合,利用预测控制方法对无人机的运动进行预测,从而在实现实时性的同时避免碰撞。此外,也可以引入一些约束条件来限制无人机的运动范围,从而保证队形的稳定性。这些方法为基于匈牙利算法实现无人机编队队形的实时切换提供了一些思路。
总的来说,基于匈牙利算法实现无人机编队队形的实时切换是一个具有挑战性的课题,但也是具有很大潜力的研究方向。随着无人机技术的不断发展和成熟,相信基于匈牙利算法的无人机编队技术将会得到更广泛的应用,并为无人机的协同作战能力和应用价值带来新的突破。
📣 部分代码
clc;clear all;% 做 8*8 矩阵 19 个点 字符:Farray_f = [0 1 1 1 1 1 1 0;0 0 1 0 0 0 0 0;0 0 1 0 0 1 0 0;0 0 1 1 1 1 0 0;0 0 0 0 0 1 0 0;0 0 1 0 0 0 0 0;0 0 1 0 0 0 0 0;0 1 1 1 0 0 0 0];% 做 8*8 矩阵 19 个点 字符:Zarray_z = [0 1 1 1 1 1 1 0;0 1 0 0 0 1 0 0;0 0 0 0 1 0 0 0;0 0 0 1 0 0 0 0;0 0 0 1 0 0 0 0;0 0 1 0 0 0 0 0;0 0 0 0 0 1 0 0;1 1 1 1 1 1 0 0];%% showfigure(1)% for i=1:8% for j=1:8% if array_f(i,j)==1% plot([j],[8-i],'bo');% hold on;% end% end% end%% figure(2)% for i=1:8% for j=1:8% if array_z(i,j)==1% plot([j],[8-i],'bo');% hold on;% end% end% end%% FZ矩阵转换T0T1%F矩阵转换为坐标T0:T0=zeros(19,3);n = 1;for i=1:8for j=1:8if array_f(i,j) == 1T0(n,:) = [i,j,0];n = n + 1;endendend%Z矩阵转换为坐标T1:T1=zeros(19,3);n = 1;for i=1:8for j=1:8if array_z(i,j) == 1T1(n,:) = [i,j,0];n = n + 1;endendend%% 显示结果% for i=1:19% for j=1:19% if a(i,j) == 1 && ~isequal(T0(i,:), T1(j,:))% axis([0 10 0 10]);% plot(T0(i,2),9-T0(i,1),'go');% hold on;% plot(T1(j,2),9-T1(j,1),'ro');% hold on;% plot([T0(i,2),T1(j,2)],[9-T0(i,1),9-T1(j,1)]);% hold on;%% end% end% end%% 对应关系for i=1:19for j=1:19if a(i,j) == 1A(i,:)=[T0(i,2),9-T0(i,1)];B(i,:)=[T1(j,2),9-T1(j,1)];endendend%% 动态显示结果run(A,B);
⛳️ 运行结果
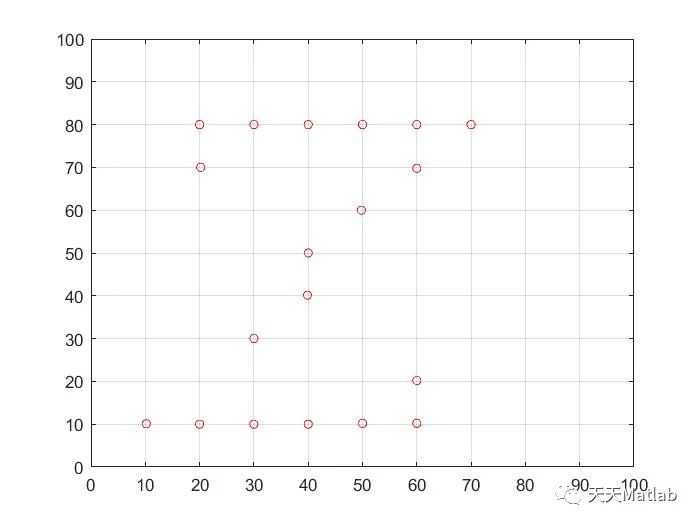
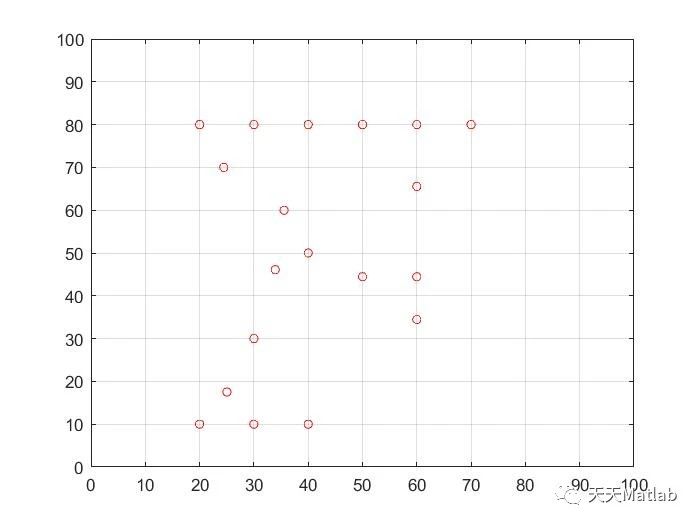
🔗 参考文献
[1] 盛汉霖,叶勇杰,李嘉诚,等.一种基于匈牙利算法的多无人机编队航迹规划方法:CN201810501648.5[P].CN108733074A[2023-12-19].
[2] 姜鸿儒,范云锋,徐亚周,等.基于动态角色分配的一致性协同无人机编队控制[J].计算机测量与控制, 2023, 31(5):126-131.








 文章探讨了如何利用匈牙利算法解决无人机编队队形的实时切换问题,构建成本矩阵考虑因素,结合预测控制和约束条件以实现稳定性,同时面临实时性和动态环境的挑战。
文章探讨了如何利用匈牙利算法解决无人机编队队形的实时切换问题,构建成本矩阵考虑因素,结合预测控制和约束条件以实现稳定性,同时面临实时性和动态环境的挑战。


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










