【路径规划-TSP问题】基于粒子群求解旅行商问题附Matlab代码

 ✅作者简介：热爱数据处理、建模、算法设计的Matlab仿真开发者。

🍎更多Matlab代码及仿真咨询内容点击 🔗：Matlab科研工作室

🍊个人信条：格物致知。

🔥 内容介绍

1. 旅行商问题概述

旅行商问题（TSP）是一个经典的组合优化问题，它描述了一个旅行商需要访问一组城市，并且希望找到一条最短的路径，使得他可以访问所有城市并返回起点。TSP在现实生活中有很多应用，例如物流配送、车辆调度和电路板布线等。

2. 粒子群算法概述

粒子群算法（PSO）是一种受鸟群觅食行为启发的群体智能算法。在PSO中，每个粒子代表一个潜在的解决方案，粒子群则代表一组潜在的解决方案。每个粒子都有自己的位置和速度，并且会根据自己的经验和群体中其他粒子的经验来更新自己的位置和速度。

3. 基于PSO求解TSP

为了使用PSO求解TSP，我们需要将TSP问题编码成粒子群算法能够处理的形式。一种常见的方法是使用二进制编码，其中每个城市由一个二进制字符串表示，字符串的长度等于城市的数量。每个字符串的第i位表示旅行商是否在第i个城市停留。

接下来，我们需要定义PSO算法的适应度函数。适应度函数用于衡量粒子的质量，并且是粒子更新自己位置和速度的基础。对于TSP，我们可以使用路径长度作为适应度函数。

最后，我们需要设置PSO算法的参数。这些参数包括种群规模、迭代次数和惯性权重等。种群规模是指粒子群中粒子的数量，

📣 部分代码

%% 该文件演示基于TSP-PSO算法clc;clear​%% 下载数据data=load('eil51.txt');cityCoor=[data(:,2) data(:,3)];%城市坐标矩阵​figureplot(cityCoor(:,1),cityCoor(:,2),'ms','LineWidth',2,'MarkerEdgeColor','k','MarkerFaceColor','g')legend('城市位置')ylim([4 78])title('城市分布图','fontsize',12)xlabel('km','fontsize',12)ylabel('km','fontsize',12)%ylim([min(cityCoor(:,2))-1 max(cityCoor(:,2))+1])​grid on​%% 计算城市间距离n=size(cityCoor,1);            %城市数目cityDist=zeros(n,n);           %城市距离矩阵for i=1:n    for j=1:n        if i~=j

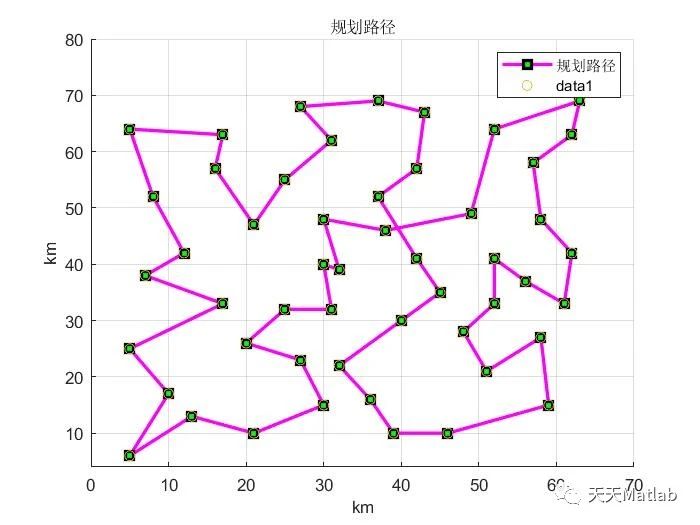
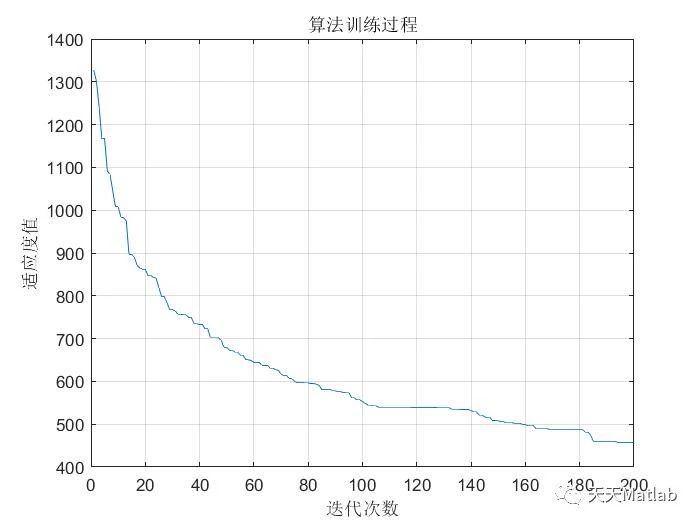
⛳️ 运行结果

🔗 参考文献

[1] 谭皓,王金岩,何亦征,等.一种基于子群杂交机制的粒子群算法求解旅行商问题[J].系统工程, 2005, 23(4):5.DOI:10.3969/j.issn.1001-4098.2005.04.017.

[2] 莫愿斌,陈德钊,胡上序.粒子群复形法求解旅行商问题[J].浙江大学学报：工学版, 2007, 41(3):5.DOI:10.3785/j.issn.1008-973X.2007.03.001.

🎈 部分理论引用网络文献，若有侵权联系博主删除

🎁  关注我领取海量matlab电子书和数学建模资料

👇  私信完整代码、论文复现、期刊合作、论文辅导及科研仿真定制

1 各类智能优化算法改进及应用

生产调度、经济调度、装配线调度、充电优化、车间调度、发车优化、水库调度、三维装箱、物流选址、货位优化、公交排班优化、充电桩布局优化、车间布局优化、集装箱船配载优化、水泵组合优化、解医疗资源分配优化、设施布局优化、可视域基站和无人机选址优化

2 机器学习和深度学习方面

卷积神经网络（CNN）、LSTM、支持向量机（SVM）、最小二乘支持向量机（LSSVM）、极限学习机（ELM）、核极限学习机（KELM）、BP、RBF、宽度学习、DBN、RF、RBF、DELM、XGBOOST、TCN实现风电预测、光伏预测、电池寿命预测、辐射源识别、交通流预测、负荷预测、股价预测、PM2.5浓度预测、电池健康状态预测、水体光学参数反演、NLOS信号识别、地铁停车精准预测、变压器故障诊断

2.图像处理方面

图像识别、图像分割、图像检测、图像隐藏、图像配准、图像拼接、图像融合、图像增强、图像压缩感知

3 路径规划方面

旅行商问题（TSP）、车辆路径问题（VRP、MVRP、CVRP、VRPTW等）、无人机三维路径规划、无人机协同、无人机编队、机器人路径规划、栅格地图路径规划、多式联运运输问题、车辆协同无人机路径规划、天线线性阵列分布优化、车间布局优化

4 无人机应用方面

无人机路径规划、无人机控制、无人机编队、无人机协同、无人机任务分配、无人机安全通信轨迹在线优化

5 无线传感器定位及布局方面

传感器部署优化、通信协议优化、路由优化、目标定位优化、Dv-Hop定位优化、Leach协议优化、WSN覆盖优化、组播优化、RSSI定位优化

6 信号处理方面

信号识别、信号加密、信号去噪、信号增强、雷达信号处理、信号水印嵌入提取、肌电信号、脑电信号、信号配时优化

7 电力系统方面

微电网优化、无功优化、配电网重构、储能配置

8 元胞自动机方面

交通流 人群疏散 病毒扩散 晶体生长

9 雷达方面

卡尔曼滤波跟踪、航迹关联、航迹融合