[NOIP2015 提高组] 子串（线性dp）

[NOIP2015 提高组] 子串

题目背景

NOIP2015 Day2T2

题目描述

有两个仅包含小写英文字母的字符串 $A$ 和 $B$。

现在要从字符串 $A$ 中取出 $k$ 个互不重叠的非空子串，然后把这 $k$ 个子串按照其在字符串 $A$ 中出现的顺序依次连接起来得到一个新的字符串。请问有多少种方案可以使得这个新串与字符串 $B$ 相等？

注意：子串取出的位置不同也认为是不同的方案。

输入格式

第一行是三个正整数 $n,m,k$，分别表示字符串 $A$ 的长度，字符串 $B$ 的长度，以及问题描述中所提到的 $k$，每两个整数之间用一个空格隔开。

第二行包含一个长度为 $n$ 的字符串，表示字符串 $A$。

第三行包含一个长度为 $m$ 的字符串，表示字符串 $B$。

输出格式

一个整数，表示所求方案数。

由于答案可能很大，所以这里要求输出答案对 $1000000007$ 取模的结果。

样例 #1

样例输入 #1

6 3 1 
aabaab 
aab

样例输出 #1

2

样例 #2

样例输入 #2

6 3 2 
aabaab 
aab

样例输出 #2

7

样例 #3

样例输入 #3

6 3 3 
aabaab 
aab

样例输出 #3

7

提示

样例解释

所有合法方案如下：（加下划线的部分表示取出的字串）

样例 1：$\text{aabaab,aabaab}$。
样例 2：$\text{aabaab,aabaab,aabaab,aabaab,aabaab,aabaab,aabaab}$。
样例 3：$\text{aabaab,aabaab,aabaab,aabaab,aabaab,aabaab,aabaab}$。

数据范围

对于第 1 组数据：$1\le n\le 500,1\le m\le 50,k=1$;
对于第 2 组至第 3 组数据：$1\le n\le 500,1\le m\le 50,k=2$;
对于第 4 组至第 5 组数据：$1\le n\le 500,1\le m\le 50,k=m$;
对于第 1 组至第 7 组数据：$1\le n\le 500,1\le m\le 50,1\le k\le m$;
对于第 1 组至第 9 组数据：$1\le n\le 1000,1\le m\le 100,1\le k\le m$;
对于所有 10 组数据：$1\le n\le 1000,1\le m\le 200,1\le k\le m$。

思路

P2679 字串

评价：这道题虽然代码短，但思维量非常大。

题意：就是给你字符串a和字符串b，然后从a中取出k个子串，问能和b匹配的子串个数。

第一眼看到这题的时候，感觉它很像最短编辑距离，因此我自己想到的是这样的：f[ i ][ j ][ k ] = f[ i-1 ][ j-1 ][ k ] + f[ i-1 ][ j-1 ][ k-1 ]； ( A[i] == B[j] )

见图：（初始想法）

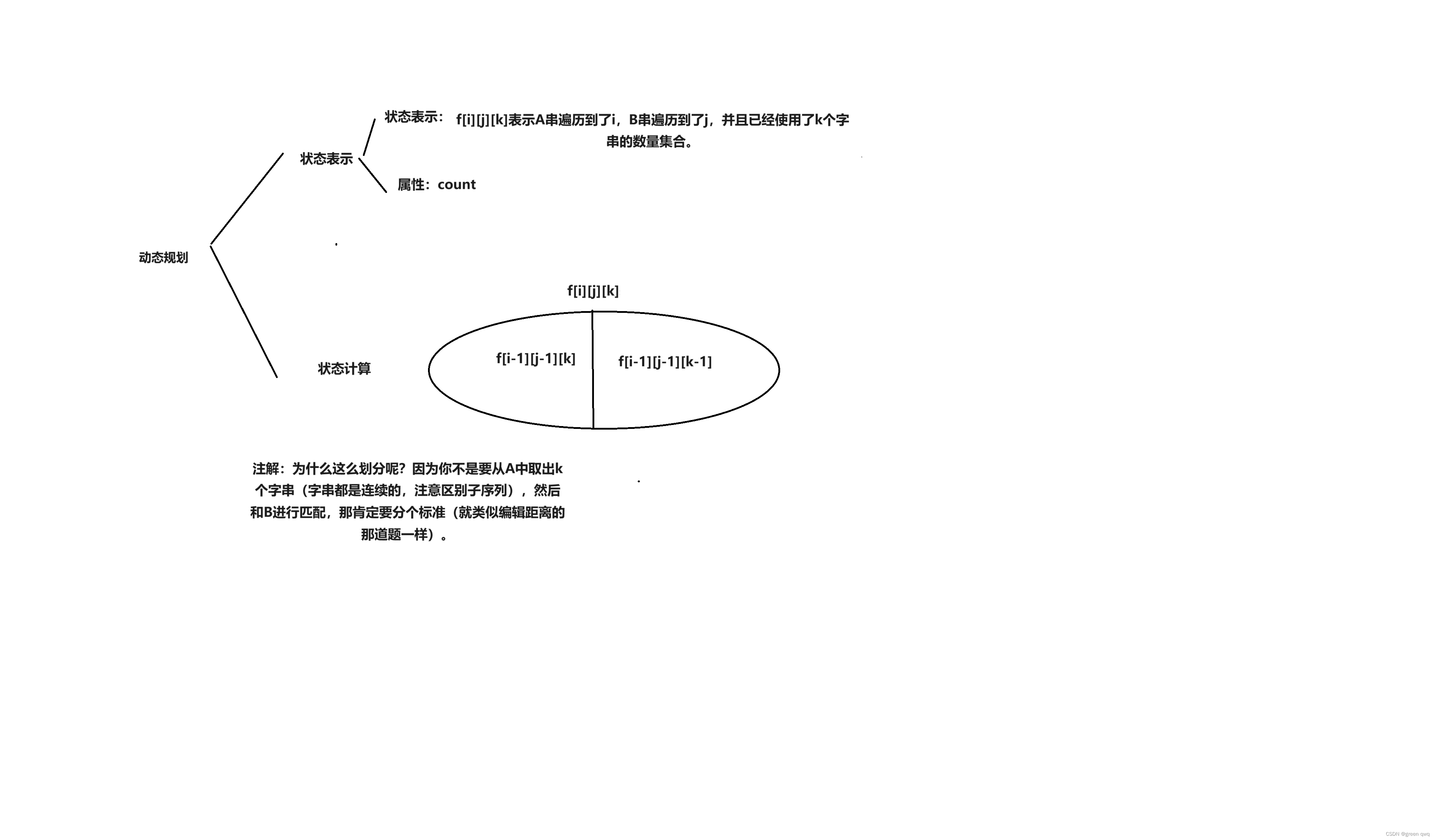
也就说：能匹配时，方案数为：单独使用当前字符为一个子串 + 与前面相连形成一个子串;

但这个DP式子是有问题的。如果不使用当前字符，情况是什么样的呢？

所以我们就要分开来设了（因为这道题它可以划分多个子串（之前最短编辑距离的那种貌似只有一个子串），此时就得用两个数组啦）。

设g[ i ][ j ][ k ]为A用到了 i ，B用到了 j ，已经用了 k 个子串， 并且一定用了当前字符(A[i])时的方案数。

设f[ i ][ j ][ k ]为A用到了 i ，B用到了 j ，已经用了 k 个子串， 无论用不用当前字符(A[i])时的方案数总和。

以上这个思路很重要。（对于这种类似最短编辑距离的题目，我们常常在dp的状态表示的时候加个“且使用A[i]”，也就是A[i]一定被用了，其实那个用不用的那个一般很少说）

一下是状态转移的推导：

---

先分析一下 g 的转移。能转移的前提自然是 A[ i ] == B [ j ]啦。既然 A[i] 一定要用，那么依旧是两种情况：独自成一串 或 与前面的成一串。

独自成一串就是图中（你也可以看题目的样例解析）的a，与前面成一串就是ab。

独自成一串，方案数为：f[ i-1 ][ j-1 ][ k-1]。（前面的爱用不用）

与前方共成一串，方案数为：g[ i-1 ][ j-1 ][ k ]，因为前一个字符串(A[i-1])也一定要用！（看图（或者看样例解释）可知）所以我们合并一下： g[ i ][ j ][ k ] = f[ i-1 ][ j-1 ][ k-1 ] + g[ i-1 ][ j-1 ][ k ]；

---

接着分析 f 的转移。（同理刚刚所说的）f[ i ][ j ][ k ] 的来源也有两种：
使用当前字符 或 不使用当前字符

对于使用当前字符，方案数算法如上，答案即：s[ i ][ j ][ k ]；

对于不使用当前字符，则从f[ i-1 ]转来，即：f[ i -1 ][ j ][ k ]；合并一下： f[ i ][ j ][ k ] = f[ i-1 ][ j ][ k ] + s[ i ][ j ][ k ]；

所以将两个合并一下子，就得到：

        if(a[i]==b[j]){
            g[i][j][k] = f[i-1][j-1][k-1] + g[i-1][j-1][k];
            f[i][j][k] = f[i-1][j][k] + g[i][j][k];
        }else g[i][j][k] = 0;
    

答案存在f[ n ][ m ][ k ]中，显然边界条件为 f[ i ][ 0 ][ 0 ] = 1；（这个是必然的，对于这种方案数的，我们边界情况通常设1）。

然后

我们可以优化，因为你不觉得第一维度很像是01背包吗，对于这样的我们可以把它优化掉：写成：

    f[0][0]=g[0][0]=1;
    
        for(int i=1;i<=n;i++){
            for(int j=m;j>=1;j--){
                for (int k=1;k<=k1;k++){
                    if (a[i]==b[j]){
                        f[j][k]=(f[j-1][k]%mod+g[j-1][k-1]%mod)%mod;
                        g[j][k]=(g[j][k]%mod+f[j][k]%mod)%mod;
                    }
                    else f[j][k]=0;
                }
            }
        }

代码

#include<cstdio>

using namespace std;

const int N = 1010,mod=1e9+7;

char a[N],b[N];
int n,m,k1,f[N][N],g[N][N];

int main(){
    scanf("%d%d%d",&n,&m,&k1);
    
    scanf("%s%s",a+1,b+1);
    
    f[0][0]=g[0][0]=1;
    
    for(int i=1;i<=n;i++){
        for(int j=m;j>=1;j--){
            for (int k=1;k<=k1;k++){
                if (a[i]==b[j]){
                    f[j][k]=(f[j-1][k]%mod+g[j-1][k-1]%mod)%mod;
                    g[j][k]=(g[j][k]%mod+f[j][k]%mod)%mod;
                }
                else f[j][k]=0;
            }
        }
    }
    printf("%d",g[m][k1]);
    return 0;
}