前缀和差分（一维+二维）

已于 2022-07-16 00:05:37 修改
阅读量405 收藏
点赞数
分类专栏： 前缀和差分 STL 文章标签： 算法 c++
于 2022-07-16 00:02:13 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/m0_60777643/article/details/125812648
版权

目录

1.一维前缀和

2.一维差分

一维差分数组初始化

差分标记区间

恢复原数组（一维前缀和）

3.二维前缀和

二维前缀和初始化

 子矩形的前缀和

 4.二维差分

初始化差分

标记区间

复原差分数组（对差分矩阵取前缀和）

1.一维前缀和

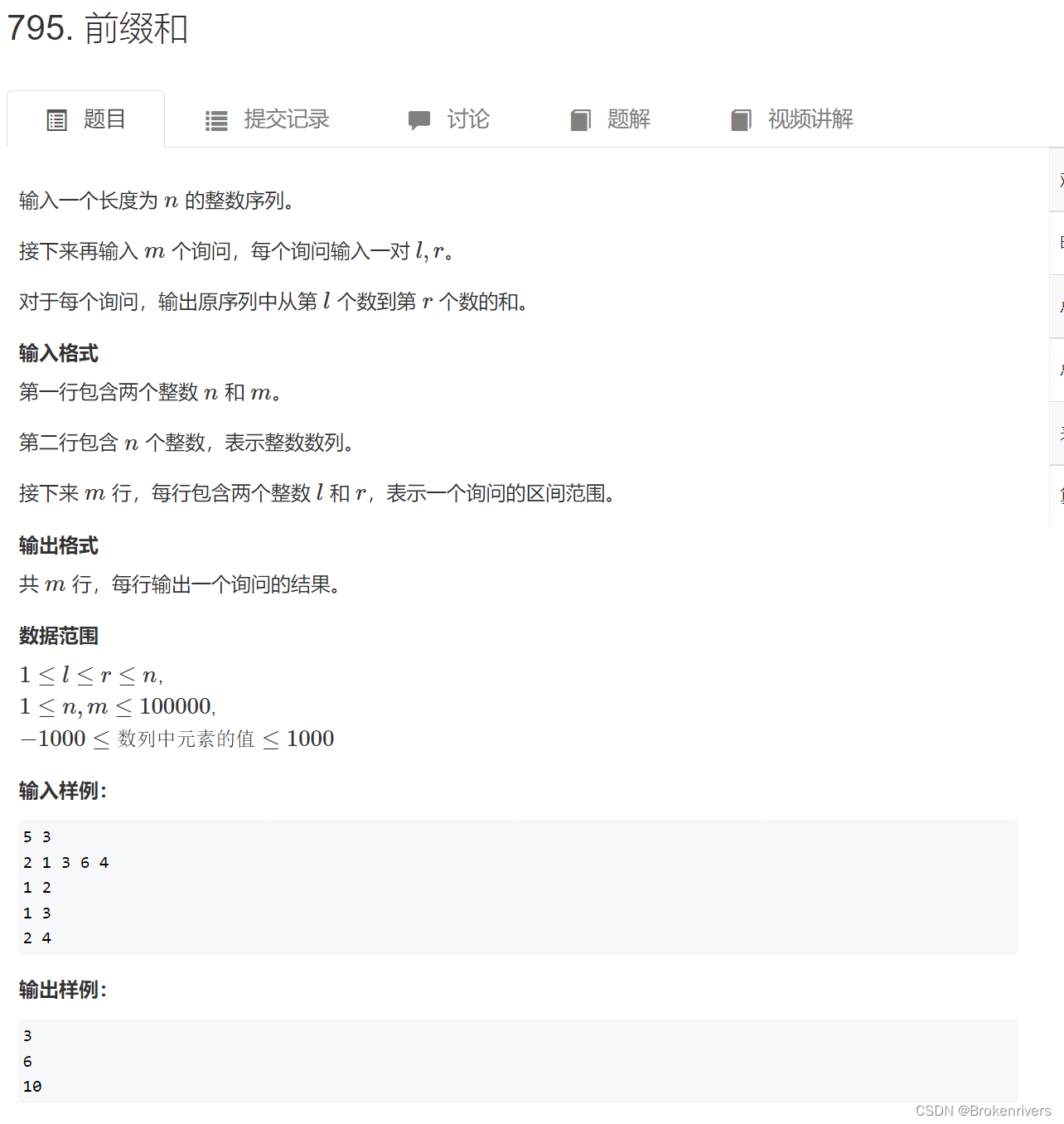
一维还是很好理解的，对原数组求和，前缀和每个元素表示之前所有元素的总和。累加即可

#include <bits/stdc++.h>
#include<iostream>
#include<thread>
using namespace std;
#pragma warning(disable:4996);
#define ll long long
#define	int ll
#define endl "\n"
#define rep(j,b,e) for(int j=b;j<=e;j++)
#define eb(arr) arr.begin(),arr.end()
#define mm(arr) memset(arr,0,sizeof(arr))
#define get(a,node) get<a-1>(node)
int T;
const int N = 2e5 + 10;
int n, k, q;
void inline  inln() {}
template<class T, class ...Arg>
void inline  inln(T& t, Arg&...args) {
	cin >> t;
	inln(args...);
}
void inline pln() {
	cout << "\n";
}
template <class T, class ...Arg>
void inline pln(T t, Arg ...args) {
	cout << t << " ";
	pln(args...);
}
template<typename T>
void inline pln(vector<T>& a, string s = " ") {
	for (T& x : a) {
		cout << x << s;
	}
	cout << endl;
}

signed main()
{
#ifndef ONLINE_JUDGE
	//freopen("out.txt", "w", stdout);
#endif
	inln(n, k);
	vector<int>sum(1);
	rep(j, 1, n) {
		int t;
		cin >> t;
		sum.push_back(sum[j - 1] + t);
	}
	rep(j, 1, k) {
		int l, r;
		inln(l, r);
		pln(sum[r] - sum[l - 1]);
	}
	return 0;
}

2.一维差分

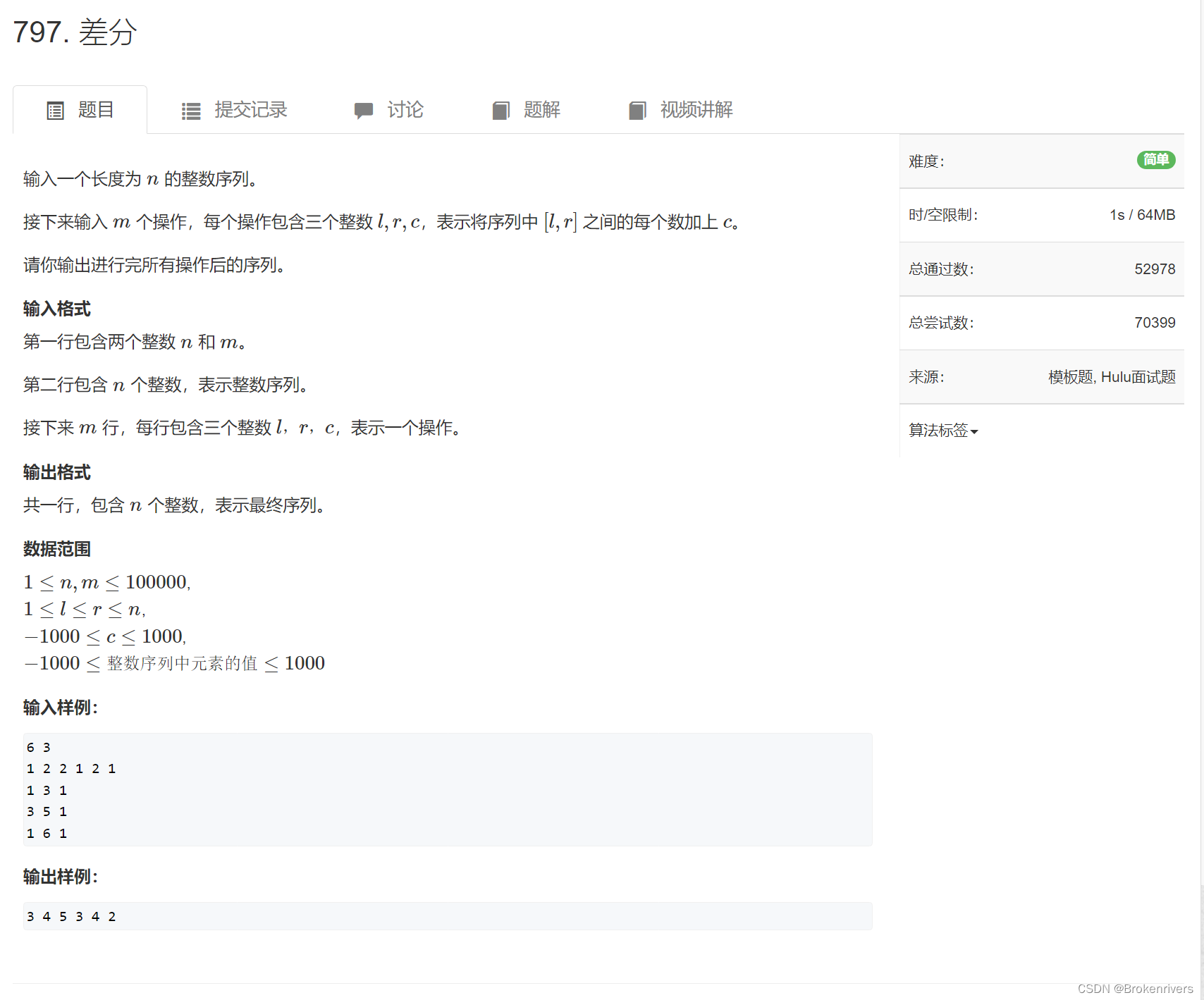
 差分也就是前缀和的逆运算，多用于对区间标记O(1)的处理整个区间的操作。

一维差分数组初始化

对前缀和公式移项：

sum[i] = sum[i-1]+arr[i]  -->   arr[i] = sum[i]-sum[i-1]

数学意义就是sn-sn-1=an

此时arr被称为差分数组

可以看出差分和前缀和其实是互逆得到操作。

差分标记区间

如果要使[l,r]区间上每个元素a[i] 都加上C，

可以先得到a的差分数组b

因为a是b的前缀和，所以满足

a[i]=sum(b[1],b[2]....b[i])

如果使b[i]=b[i]+C

那么a数组中i之前的元素都没有变化，i之后的元素全部+C

这个很简单，如果使b[i]=b[i]+C，那么a[1],a[2]...a[i-1]都跟b[i]没关系，所以不改变

但是a[i],a[i+1],a[n] 因为都加上了b[i]所以值全部+C

而我们需要加C的区间为[l,r]，所以令b[l]=b[l]+C，同时还需要让b[r+1]=b[r+1]-C。

看图就很好理解为什么b[r+1]需要-C了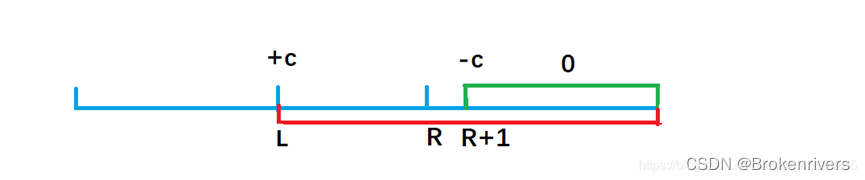

dif[l] += c;
dif[r + 1] -= c; 

要注意差分标记时，只影响后面的原数组，二维差分也是如此。

恢复原数组（一维前缀和）

#include <bits/stdc++.h>
#include<iostream>
#include<thread>
using namespace std;
#pragma warning(disable:4996);
#define ll long long
#define	int ll
#define endl "\n"
#define rep(j,b,e) for(int j=b;j<=e;j++)
#define eb(arr) arr.begin(),arr.end()
#define mm(arr) memset(arr,0,sizeof(arr))
#define get(a,node) get<a-1>(node)
int T;
const int N = 2e5 + 10;
int n, k, q;
void inline  inln() {}
template<class T, class ...Arg>
void inline  inln(T& t, Arg&...args) {
	cin >> t;
	inln(args...);
}
void inline pln() {
	cout << "\n";
}
template <class T, class ...Arg>
void inline pln(T t, Arg ...args) {
	cout << t << " ";
	pln(args...);
}
template<typename T>
void inline pln(vector<T>& a, string s = " ") {
	for (T& x : a) {
		cout << x << s;
	}
	cout << endl;
}


signed main()
{
#ifndef ONLINE_JUDGE
	//freopen("out.txt", "w", stdout);
#endif
	inln(n, k);
	vector<int>arr(1);
	vector<int>dif(N, 0);
	rep(j, 1, n) {
		int t;
		cin >> t;
		arr.push_back(t);
		dif[j] = arr[j] - arr[j - 1];//预处理的差分数组
	}
	while (k--) {
		int l, r, c;
		inln(l, r, c);
		dif[l] += c;//标记区间
		dif[r + 1] -= c;//差分
	}
	rep(j, 1, n) {
		dif[j] += dif[j - 1];//前缀和
		cout << dif[j] << " ";
	}
	return 0;
}

3.二维前缀和

 二维前缀和更难理解一些

二维前缀和初始化

sum[i][j]的前缀和为 蓝色矩形的和

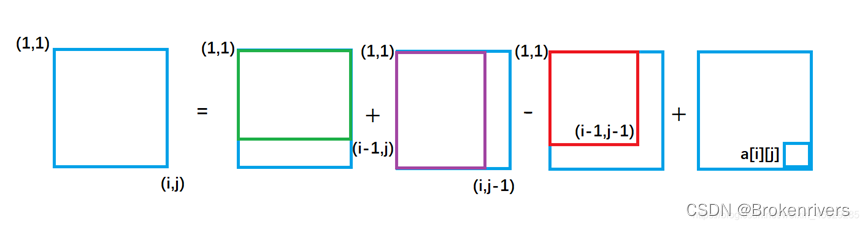
因此得出二维前缀和预处理公式

s[ i ] [ j ] = s[ i-1 ][ j ] + s[ i ] [ j-1 ] + a[ i ] [ j ] - s[ i-1 ][ j-1 ]

------------------------------

 子矩形的前缀和

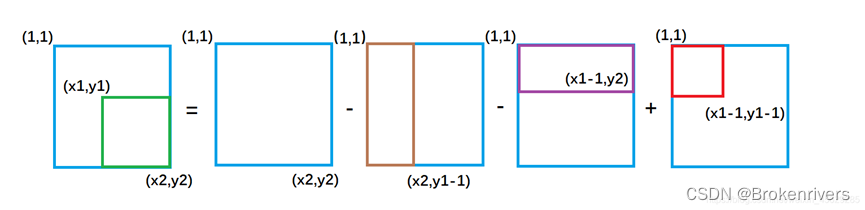
因此二维前缀和的结论为：

以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵的和为：

s[x2, y2] - s[x1 - 1, y2] - s[x2, y1 - 1] + s[x1 - 1, y1 - 1]

#include <bits/stdc++.h>
#include<iostream>
#include<thread>
using namespace std;
#pragma warning(disable:4996);
#define ll long long
#define	int ll
#define endl "\n"
#define rep(j,b,e) for(int j=b;j<=e;j++)
#define eb(arr) arr.begin(),arr.end()
#define mm(arr) memset(arr,0,sizeof(arr))
#define get(a,node) get<a-1>(node)
int T;
const int N = 2e5 + 10;
int n, m, k, q;

template <class T, class ...Arg>
void inline pln(T t, Arg ...args);//打印一行参数
template<typename T>
void inline pln(vector<T>& a, string s = " ");
template<class T, class ...Arg>
void inline  inln(T& t, Arg&...args);//输入一行数据
//---------------------------
signed main()
{
#ifndef ONLINE_JUDGE
	freopen("out.txt", "w", stdout);
#endif
	inln(n, m, k);
	vector<vector<int>>sum(1001, vector<int>(1001, 0));
	rep(j, 1, n) {
		rep(i, 1, m) {
			int t;
			cin >> t;
			sum[j][i] = sum[j - 1][i] + sum[j][i - 1] - sum[j - 1][i - 1] + t;//预处理
		}
	}
	rep(j, 1, k) {
		int l1, r1, l2, r2;
		inln(l1, r1, l2, r2);
		int t = sum[l2][r2] - sum[l1 - 1][r2] - sum[l2][r1 - 1] + sum[l1 - 1][r1 - 1];//子矩形和
		pln(t);
	}
	return 0;
}
//--------------------------------
void inline  inln() {}
template<class T, class ...Arg>
void inline  inln(T& t, Arg&...args) {
	cin >> t;
	inln(args...);
}
void inline pln() {
	cout << "\n";
}
template <class T, class ...Arg>
void inline pln(T t, Arg ...args) {
	cout << t << " ";
	pln(args...);
}
template<typename T>
void inline pln(vector<T>& a) {
	for (T& x : a) {
		cout << x << " ";
	}
	cout << endl;
}

 4.二维差分

二维差分算是比较复杂的过程了。

初始化差分

首先是由原矩阵得到差分数组

由一维差分的概念可知，差分矩阵的元素就是前缀和的相邻差值。也就是图中间小蓝色区域。

这段值可以由红色矩阵的和加上黄色矩阵的和减去中间重复的紫色区域。

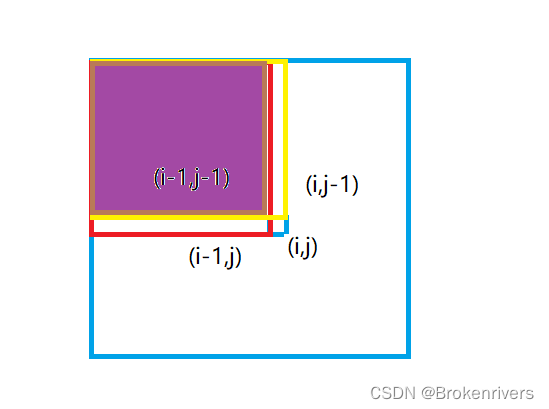
因此，设dif为差分数组，数学公式为

dif[ i ][ j ] = arr[ i ][ j ] - arr[i - 1][ j ]  - arr[i][j - 1] + arr [i - 1][j - 1]

这样就得到原始的差分数组

标记区间

标记也很复杂，但是基本逻辑和一维差分一样，某个差分元素+c，这个点对应的子矩阵元素全部+c，我们要做的不仅是(x1,y1)+c，同时还要将无关区域-c保持不变。据图就很直观了

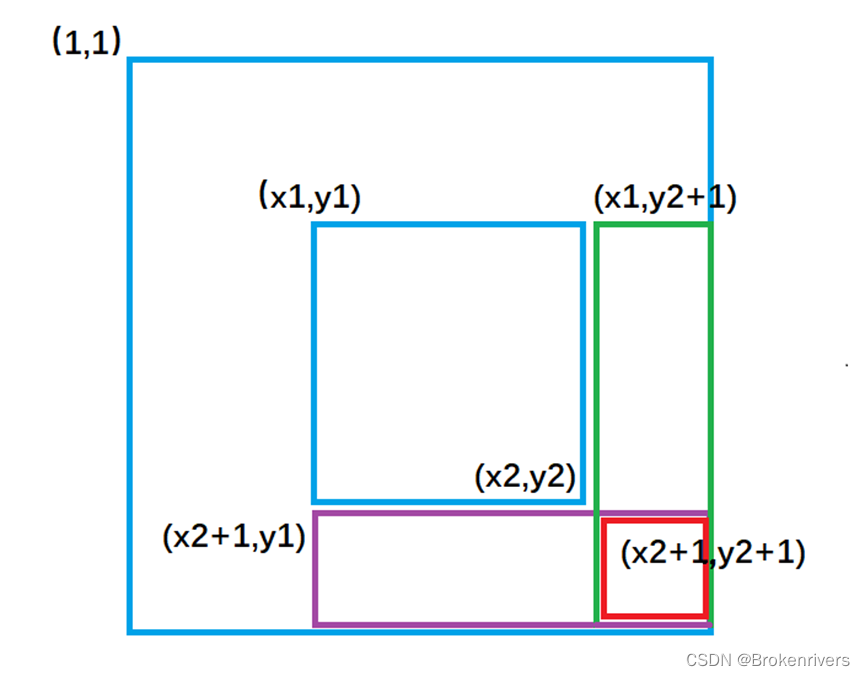
 写成数学表达就是：

dif[x1][y1] += c;
dif[x1][y2 + 1] -= c;
dif[x2 + 1][y1] -= c;
dif[x2 + 1][y2 + 1] += c;

复原差分数组（对差分矩阵取前缀和）

据图(i,j)的前缀和可由绿色+紫色+红色-紫绿重复的区间构成

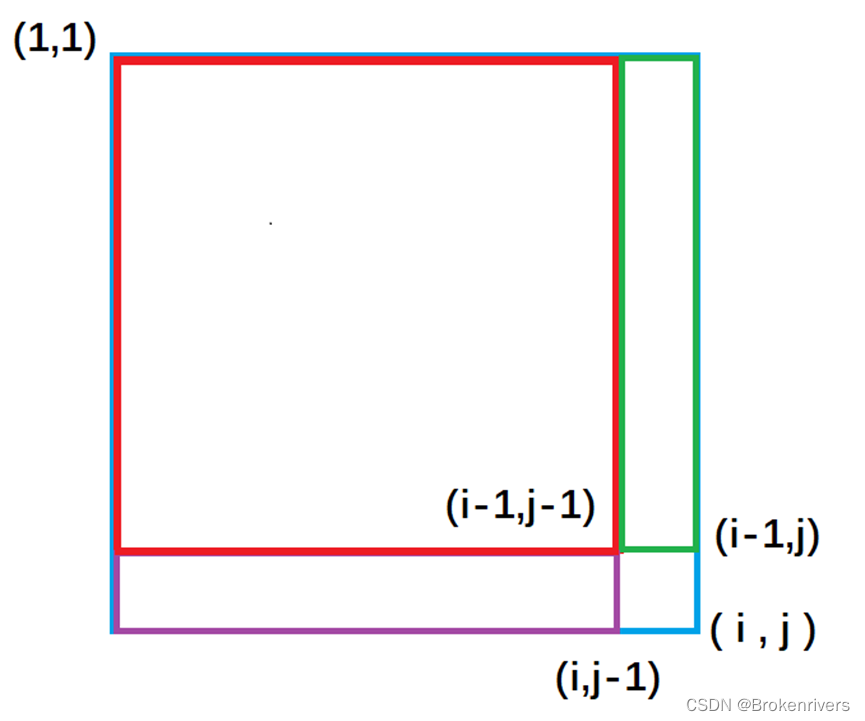
数学表达为：

dif [ i ][ j ] = dif [i - 1][ j ] + dif [ i ][j - 1] - dif [i - 1][j - 1] + dif [ i ][ j ]

#include <bits/stdc++.h>
#include<iostream>
#include<thread>
using namespace std;
#pragma warning(disable:4996);
#define ll long long
#define	int ll
#define endl "\n"
#define rep(j,b,e) for(int j=b;j<=e;j++)
#define eb(arr) arr.begin(),arr.end()
#define mm(arr) memset(arr,0,sizeof(arr))
#define get(a,node) get<a-1>(node)
int T;
const int N = 2e5 + 10;
int n, m, k, q;

template <class T, class ...Arg>
void inline pln(T t, Arg ...args);//打印一行参数
template<typename T>
void inline pln(vector<T> a, string s = " ");
template<class T, class ...Arg>
void inline  inln(T& t, Arg&...args);//输入一行数据
//----------------------------------

signed main()
{

	inln(n, m, k);
	vector<vector<int>>dif(1010, vector<int>(1010));
	auto arr = dif;
	rep(i, 1, n) {
		rep(j, 1, m) {
			int t;
			cin >> t;
			arr[i][j] = t;
            //预处理差分数组
			dif[i][j] = arr[i][j] - arr[i - 1][j] - arr[i][j - 1] + arr[i - 1][j - 1];
		}
	}
	rep(j, 1, k) {
		int x1, y1, x2, y2, c;
		inln(x1, y1, x2, y2, c);
		dif[x1][y1] += c;
		dif[x1][y2 + 1] -= c;
		dif[x2 + 1][y1] -= c;
		dif[x2 + 1][y2 + 1] += c;//差分,差分标记影响的是后面的区域
	}
	rep(i, 1, n) {
		rep(j, 1, m) {
			dif[i][j] = dif[i - 1][j] + dif[i][j - 1] - dif[i - 1][j - 1] + dif[i][j];
            //求差分数组的前缀和，复原
		}
	}
	rep(i, 1, n) {
		pln(vector<int>(dif[i].begin() + 1, dif[i].begin() + m + 1));
	}
	return 0;
}
//-------------------------------------

void inline  inln() {}
template<class T, class ...Arg>
void inline  inln(T& t, Arg&...args) {
	cin >> t;
	inln(args...);
}
void inline pln() {
	cout << "\n";
}
template <class T, class ...Arg>
void inline pln(T t, Arg ...args) {
	cout << t << " ";
	pln(args...);
}
template<typename T>
void inline pln(vector<T> a, string s) {
	for (T& x : a) {
		cout << x << s;
	}
	cout << endl;
}

Brokenrivers
关注
  • 0
    点赞
  • 踩
  • 0
    收藏
    觉得还不错? 一键收藏
  • 0
    评论
专栏目录
某学长讲课ppt（前缀和与差分，二维前缀和与差分）
03-23
二维前缀和与差分的计算：在一维的基础上，进一步讲解二维前缀和与差分的计算方法，结合图表和实例，展现其在图像处理、矩阵计算等领域的应用价值。 应用示例：通过算法竞赛、数据处理等实际场景中的应用案例，展示...
前缀和与差分算法地深入理解
07-11
本文将深入讨论前缀和的概念、二维前缀和、差分和差分矩阵，并探讨它们在算法设计中的应用。 一、前缀和 前缀和是指数组中某个位置之前的元素之和。设数组a：a[1],a[2],…,a[n]，则其前缀和数组s：s[i] = a[1] + a...
前缀和与差分数组 (一维和二维)
weixin_43876403的博客
01-10 534
前言：今天写题目的时候遇到了一个二维差分的题目，由于之前没有接触过，因此前来记录一下 前缀和 差分通常需要和前缀和一起使用才能发挥奇效，所以我们先来介绍一下前缀和。 一维前缀和：对于一个长度为 nnn 的数组 arrarrarr , 前缀和数组的定义为 sum[i+1]=sum[i]+arr[i]sum[i + 1] = sum[i] + arr[i]sum[i+1]=sum[i]+arr[i], 其中 i∈[0,n)i \in [0, n)i∈[0,n). 二维前缀和：对于一个行数为 mmm 列
前缀和（c++实现）
qq_59429217的博客
03-30 3208
一维前缀和与二维前缀和
差分详细讲解(C++)
weixin_73888239的博客
12-20 7977
还不会差分吗?本文详细介绍了差分的应用和构造
差分（一维，二维）
weixin_56265979的博客
11-08 359
差分算法
差分的运算
Dankon的博客
08-29 707
差分 输入一个长度为 n 的整数序列。 接下来输入 m 个操作，每个操作包含三个整数 l,r,c，表示将序列中 [l,r] 之间的每个数加上 c。 请你输出进行完所有操作后的序列。 输入格式 第一行包含两个整数 n 和 m。 第二行包含 n 个整数，表示整数序列。 接下来 m 行，每行包含三个整数 l，r，c，表示一个操作。 输出格式 共一行，包含 n 个整数，表示最终序列。 数据范围 1≤n,m≤100000, 1≤l≤r≤n, −1000≤c≤1000, −1000≤整数序列中元素的值≤1000 输入
关于区间操作查找（前缀和与差分）+树状数组基础.doc
07-09
关于区间操作查找（前缀和与差分）+树状数组基础 本文主要介绍了前缀和与差分的概念，以及树状数组的基础知识。前缀和是一种数组中某元素之前（包括此元素）的所有元素的和，可以用来快速计算区间和。差分是将当前...
纪中训练5月2日提高组反思
01-19
二维差分+二维前缀和+暴力统计 T2（The Great Revegetation） 首先我通过推算得到，答案是2连通块的个数 有关关系的，我就想到了并查集记录关系，也就是友好（相同草）和敌对（不同草） 但是一个并查集无法记录连通...
gasstationleetcode-binary-search:二分查找
06-30
搜索已排序的二维数组 搜索未知大小 固定点 排序数组中的单个元素 等差数列中缺少数字 缺少元素 有效的山数组 山谷的顶峰 在 Mountain Array 中查找 峰元素 在旋转数组中找到最小值 在旋转数组中搜索 平方根 有效的...
一维差分保姆级入门教程（第一章）
MGherobrine的博客
11-18 205
常见的一维差分操作是令某一段区间的数同时加上一个数，我们利用定义出发很容易就能想到只要在区间起点位置加上一个数就行了，但是这样的话我们构成的新数组就是从起点开始以后的数都加上一个数，因为我们想要的只是一段区间，所以只需要在终点的下一个位置减去这个数即可。
(C++) 基础算法学习：一维差分
m0_67839004的博客
02-05 139
【代码】(C++) 基础算法学习：差分。
C++前缀和（一维）
zbq3025456153的博客
10-30 232
【代码】C++前缀和（一维）
[AcWing] 797. 差分（算法基础课）（C++实现）一维差分模板题
cloud的博客
11-01 806
[AcWing]796. 子矩阵的和（C++实现）二维前缀和模板题1. 题目2. 读题（需要重点注意的东西）3. 解法4. 可能有帮助的前置习题5. 所用到的数据结构与算法思想6. 总结 1. 题目 2. 读题（需要重点注意的东西） 思路：二维前缀和，多用于求区间和，能将O(n)的时间复杂度转换为O(1)； 关键代码在于 求前缀和 求区间和：左上角的坐标为(x1,y1),右下角的坐标为(x2,y2),求此区间的和的公式为 3. 解法 --------------------------
二维差分
weixin_30437481的博客
04-22 315
　　二维差分和一维差分思路上并没有什么区别，具体实现的区别就在于一维的直接对区间两端差分就好了，而二维的多了一维需要处理。 　　差分的思想是和前缀和有关的，一维的前缀和我们都懂求，那么二维的呢？ 　　如图 　　因为是从左到右，从上到下的遍历，当要求红色部分，(0,0)到（i,j）处的前缀和时，我们黄色部分和蓝色部分已经是已知的了，而它们重叠的部分就是绿色部分，所以把黄色和蓝色部分的结果加起来...
一维差分与二维差分问题
weixin_41514525的博客
07-28 282
一维差分： 输入一个长度为n的整数序列。 接下来输入m个操作，每个操作包含三个整数l, r, c，表示将序列中[l, r]之间的每个数加上c。 请你输出进行完所有操作后的序列。 输入格式 第一行包含两个整数n和m。 第二行包含n个整数，表示整数序列。 接下来m行，每行包含三个整数l，r，c，表示一个操作。 输出格式 共一行，包含n个整数，表示最终序列。 数据范围 1≤n,m≤...
【模板】一维前缀和与一维差分
脚踏实地，仰望星空
01-29 708
1.一维前缀和 1.1 求解一维前缀和数组 1.2 区间查询 2.一维差分 2.1 定义 2.2 区间修改 2.3 初始化
差分数组C++
斯坦福-MIT-Harvard-CMU
02-13 1942
差分数组在数组某一段数值同乘以一个值，或者求某数组的前n项和非常方便 int a[] = {0,1,2,3,4,5}; b[i] = a[i] - a[i-1];(1<i≤n,b[1]=a[1],a[0] = b[0] = 0) b[ ] = {0,1,1,1,1,1} 则称b[ ]是a的差分数组，它具有的性质是a[i] = b[i] + b[i-1] + … + b[1]; 如果要在数...
二维前缀和 二维空间里面哪个是前缀和 哪个是差分
最新发布
03-14
前缀和是指对于一个二维数组，计算出每个元素左上角的所有元素之和，差分是指对于一个二维数组，计算出每个元素与其左上角元素之差。在二维空间中，前缀和通常用于计算矩阵区域内的元素和，而差分通常用于计算矩阵区域内的元素差。

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值