逻辑代数是学习数电基础。虽然实际过程中数字电路的自动化设计计数早已取代了手工处理过程,但是学习化简过程也具有重要的意义(平时作业有啊,还不给答案!),所以用C++ 写了在已知最小项和无关项情况下采用Q-M(列表化简)法,得出最简表达式。
首先看几个概念:

最小项:m=2 (0010:abCd) ; m=6 (0110:aBCd) 就是一个蕴含项,但是他们不是质蕴含项,因为他们可以合并嘛 :表示为 :aCd:0-10 (这也是逻辑代数能化简的原因)。所以最后可以不能被合并的蕴含项就是质蕴涵项。实质蕴含项就是存在一个最小项,而其它质蕴涵项中都没有这个最小项。观察发现,只有相差一位“1”的才能合并。所以先将最小项根据1的数量按照顺序排列,再合并。

开始Q-M化简 :(先考虑只有最小项的情况,无关项在完成最小项基础上加一个条件就好了(我的代码是这样的))
先定义一个类,就叫他最小项类:

注意:
Num_of_group:指的是合并组数,只有同一组才能合并。例如上图中:单个最小项:m=2和m=6是同一组,合并后m=2,6 为下一组。规定:输入的最小项为组数0,每合并一次,组数加1。
Include_LT:将合并的最小项存储起来,Include_LT_lenth:储存最小项的个数。例如:
单个输入最小项m=2, Include_LT[0]=2,Include_LT_lenth=1; 一次合并m=2,6,Include_LT[0]=2, Include_LT[1]=6, Include_LT_lenth=2;
按照上述:完成最小项的输入与储存。存到

注意:AT_lenth为储存的最小项类长度,并非输入的最小项长度。后续操作,每合并最小项一次,AT_lenth长度都会加一。
我们也将输入另外存入一个数组,方便后续使用:

注意 :Input_m数组是按照顺序存入,而Input_m_Mark[a][2]中a代表最小项数据。比如按照2,4,6...输入最小项,则Input_m[0]=2, Input_m[1]=4...Input_m_Mark[2][0]=0(最小项2的输入顺序),Input_m_Mark[2][1]=标记标志(后续操作的标志)。int Input_mLenth :输入的最小项长度;
第一步:查找质蕴涵项
完成最小项存入后,开始合并,最终得到所有的质蕴含项。两个判断:同一组,1的数量差一位就合并。将合并的新类加在AT_L末尾,并且统一将LowestTerm_m取少一位1的最小项,如m=2,6(0-10)中LowestTerm_m=2,并将被合并的最小项类合并标志combine_Flag置1;
注意:合并后,将合并位标记。如m=2 (0010) + m=6 (0110) >> m=2,6(0-10),第二位“-”。并且,合并时,对应的"-"必须一致。如:m=8,9(100-) + m=12,13(110-) >>m=8,9,12,13(1-0-)。
AT_lenth=QM_input(AT_L);
cout << "--------- 第一步查找质蕴含项 ---------" << endl;
for (int i = 0; i < AT_lenth; i++)
{
for (int j = 0; j < AT_lenth; j++)
{
//Num_of_group 同一组检测
if (AT_L[j].show_Num_of_group() == AT_L[i].show_Num_of_group())
{
//Num_of_1 差一位检测
if (AT_L[j].show_Num_of_1() - AT_L[i].show_Num_of_1() == 1)
{
combineATcheck(AT_L[i], AT_L[j]);
}
}
}
}循环结束后,我们就得到了,所有的质蕴含项:即最小项类合并标志combine_Flag为0。

但是,我们发现,质蕴含项中并不是互斥的。如最后的两组:均为1-0-,由下图可知:

经过不同组合的合并,最终可能得到一样的质蕴含项。所以我们需要检测,并去掉多余的相同质蕴含项。这里,我建立的一个新类,用于单独存储互斥的质蕴含项,就叫他质蕴含项类。

注意:RecordaddrIN_LSList:记录原最小项类数组中位置,方便返回寻找对应的最小项类。
IncLT_List[10]和IncLT_length就是最小项类中对应数组。
Real_RI_Flag:实质蕴含项的标志。
赋值到质蕴含项类数组:
//赋值质蕴含项类数组
Rime_Implication RI_list[500];
int RI_lenth=0;
void RI_list_Get()
{
for (int i = 0; i < AT_lenth; i++)
{
//判断是否为质蕴含项
if (!AT_L[i].combine_Flag)
{
//判断是否已存在相同的质蕴涵项
if (Check_New_RI(AT_L[i], RI_lenth))
{
RI_list[RI_lenth].LT_to_RI(AT_L[i], i);
RI_lenth++;
}
}
}
}打印输出,我们发现已经将重复项去除了。

好了,至此我们得到质蕴含项类数组RI_list。
第二步:建立质蕴含表,并得到实质蕴涵项。

如上图,逻辑很简单,就看看一个最小项是否只属于一个质蕴涵项,那么这个质蕴涵项就是实质蕴涵项。如m=9 就只属于m=8,9,12,13这个质蕴含项,那它就是实质蕴涵项。

我们用二维数组来存最小项属于的质蕴涵项。例如:
上图中最小项m=2属于PI2,PI3,则RI_Map[2][0]= PI2在质蕴涵项类数组中的角标,RI_Map[2][1]= PI3在质蕴涵项类数组中的角标,RI_mLenth[2]=2;
void RI_Picture()
{
//初始化
for (int i = 0; i <50; i++)
{
RI_mLenth[i] = 0;
for (int j = 0; j <50; j++)
{
RI_Map[i][j] = 0;
}
}
for (int i = 0; i < RI_lenth; i++)
{
for (int j = 0; j < RI_list[i].IncLT_length; j++)
{
//记录次最小项数值->对应 RI_Map[]和RI_mLenth[] 下标
int tmp_addr = RI_list[i].IncLT_List[j];
RI_Map[tmp_addr][ RI_mLenth [tmp_addr] ]=i;
RI_mLenth[tmp_addr]++;
}
}
}至此,我们得到了完整的质蕴含表:

现在,什么是实质蕴含项呢?很简单,就是最小项m的RI_mLenth[m]为1的对应的RI_Map[m][0]。
如上图中的m=9对应的第6个质蕴涵项:m=8,9,12,13 和m=15对应的第5个质蕴涵项:m=13,15。可见,代码结果和手画的质蕴含表结果相同。但是,完全可能没有实质蕴含项哎?这个就要看一步了,也是Q-M 化简的最后一步。
第三步:寻找最佳覆盖。
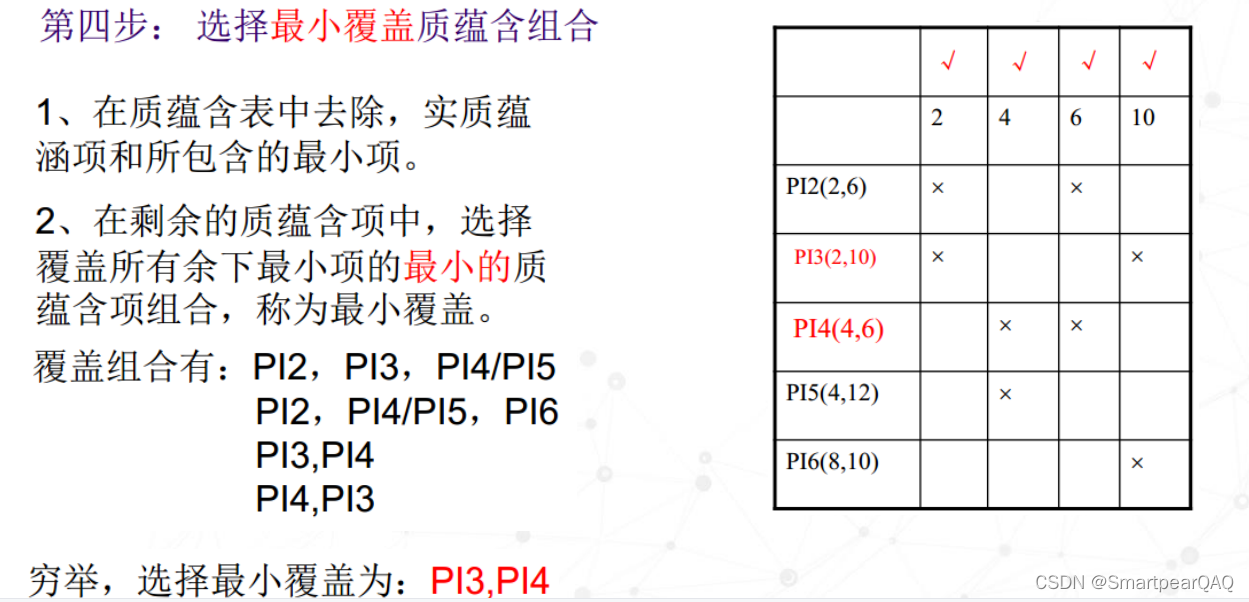
首先,我们明确什么叫最佳覆盖。就是用数量最少的质蕴涵项能包括所有的最小项,不难理解,一个质蕴涵项对应一个逻辑表达式,(如m=2,6(0-10) >> aCd),所以如果质蕴涵项数目最少,化简最后的表达式最短(“+”号最少)。
至此,我们再来理解什么是实质蕴涵项:要得到某个表达式,就要包含所有的最小项,而实质蕴涵项包含至少一个其他蕴含项没有的最小项,就代表最后结果一定有这个实质蕴含项代表的逻辑表达式。那既然包含它,那我们就索性直接把实质蕴含项包含的所有最小项和实质蕴含项本身划出表外,再来求最佳覆盖。也就是:

代码结果符合手动画图结果:

现在我们就很好回答可能存在的没有实质蕴含项的问题了。既然没有实质蕴含项,那就代表我们不能直接从质蕴含表中得出必然含的质蕴含项,那怎么办呢?很简单,直接找最佳覆盖嘛!
至此,我们终于到了真最后一步,覆盖问题。我的想法很简单,暴力枚举呗。我们在RI_Map中保存了最小项所在的每个质蕴含项位置,那我们就让待覆盖的最小项都出一个对应的地址,组合起来,得到全部组合。
例如 :上图中


对应下图中质蕴含类数组,我们发现,已经罗列全部实现覆盖的全部组合。
注意 :这里是一个典型的算法问题,感觉上很简单,但是for循环实现不了,因为不能确定剩下最小项的个数,所以采用递归的方法实现。
见:求从n个数组任意选取一个元素的所有组合 - NULL00 - 博客园;
 然后,我们再将相同地址(即同一个质蕴涵项)合并起来:
然后,我们再将相同地址(即同一个质蕴涵项)合并起来:

最佳覆盖就出来了,就是含地址最少的那个。在返回找到对应的质蕴涵项,再加上我们开始的实质蕴含项,就是完整的最佳覆盖和最简表达式了。

至此,我们再来谈谈实质蕴涵项,它其实就是简化我们求解最佳覆盖过程的,如果划掉一部分最小项和质蕴含项,那全部实现覆盖的全部组合的数量就会得到可观的减少。
最后,我们谈谈无关项是什么?无关项就是化简是可以看做0或者1,但是覆盖时不用考虑他。所以,无关项就很简单了:
在生成质蕴涵项时,使用最小项和无关项。
在生成最小项覆盖时,只使用最小项。
有同学想要源码:
https://gitee.com/smartpear/some-publicly-available-code
觉得有用的同学,麻烦给star
本人菜鸡,如有错误或者更好的想法,欢迎讨论。







 本文介绍了使用C++编程实现逻辑代数中的Q-M化简方法,通过查找质蕴含项和实质蕴含项来简化逻辑函数表达式。详细阐述了Q-M化简的步骤,包括最小项的合并、质蕴含项和实质蕴含项的判断,以及最佳覆盖的寻找。此外,还讨论了无关项在化简过程中的作用,并提供了源码链接供读者参考。
本文介绍了使用C++编程实现逻辑代数中的Q-M化简方法,通过查找质蕴含项和实质蕴含项来简化逻辑函数表达式。详细阐述了Q-M化简的步骤,包括最小项的合并、质蕴含项和实质蕴含项的判断,以及最佳覆盖的寻找。此外,还讨论了无关项在化简过程中的作用,并提供了源码链接供读者参考。

















 537
537

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










