（重制版）TSP问题——ACO蚁群算法（代码+解释）

路径构建

   伪随机比例选择规则（random proportional）：

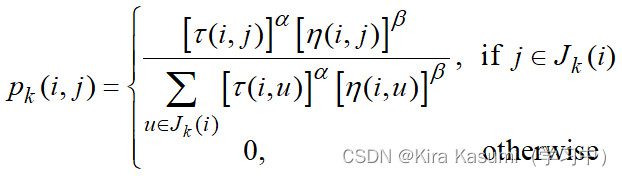
    对于每只蚂蚁k，路径记忆向量Rk按照访问顺序记录了所有k已经经过的城市序号。设蚂蚁k当前所在城市为i，则其选择城市j作为下一个访问对象的概率如上式。Jk(i)表示从城市i可以直接到达的、且又不在蚂蚁访问过的城市序列Rk中的城市集合。h(i, j)是一个启发式信息，通常由h (i, j)=1/dij直接计算。t(i, j)表示边(i, j)上的信息素量。

    长度越短、信息素浓度越大的路径被蚂蚁选择的概率越大。a和b是两个预先设置的参数，用来控制启发式信息与信息素浓度作用的权重关系。当a=0时，算法演变成传统的随机贪心算法，最邻近城市被选中的概率最大。当b=0时，蚂蚁完全只根据信息素浓度确定路径，算法将快速收敛，这样构建出的最优路径往往与实际目标有着较大的差异，算法的性能比较糟糕。

信息素更新

        （1）在算法初始化时，问题空间中所有的边上的信息素都被初始化为t0。

        （2）算法迭代每一轮，问题空间中的所有路径上的信息素都会发生蒸发，我们为所有边上的信息素乘上一个小于1的常数。信息素蒸发是自然界本身固有的特征，在算法中能够帮助避免信息素的无限积累，使得算法可以快速丢弃之前构建过的较差的路径。

        （3）蚂蚁根据自己构建的路径长度在它们本轮经过的边上释放信息素。蚂蚁构建的路径越短、释放的信息素就越多。一条边被蚂蚁爬过的次数越多、它所获得的信息素也越多。

     （ 4 ）迭代（ 2 ），直至算法终止。

m是蚂蚁个数；r是信息素的蒸发率，规定0<r≤1。 是第k只蚂蚁在它经过的边上释放的信息素量，它等于蚂蚁k本轮构建路径长度的倒数。Ck表示路径长度，它是Rk中所有边的长度和。

代码部分 

import random
import numpy as np
import matplotlib.pyplot as plt

# randomly generate the map with constraint of [-100, 100]
def gen_cities(city_num, random_state=True):
    if random_state:
        cities = (np.random.uniform(0, 2, (city_num, 2))-1)*200
        np.savetxt('cities.txt', cities)
    else:
        cities = np.loadtxt('cities.txt')
    return cities

# get distance matrix
def get_distance_mateix(cities):
    distances = np.zeros((len(cities), len(cities)))
    for i in range(len(cities)):
        for j in range(len(cities)):
            distances[i][j] = np.sqrt((cities[i][0]-cities[j][0])**2 + (cities[i][1]-cities[j][1])**2)

    return distances


# plot cities on a graph
def plot_map(cities, path):
    plt.figure(figsize=(10,10), dpi=100)
    plt.scatter(cities[:,0], cities[:,1], s=150)
    for i in range(len(cities)-1):
        plt.plot([cities[path[i]][0], cities[path[i+1]][0]], [cities[path[i]][1], cities[path[i+1]][1]], c='r')
    plt.plot([cities[path[0]][0], cities[path[len(cities)-1]][0]], [cities[path[0]][1], cities[path[len(cities)-1]][1]], c='r')
    plt.savefig('cities.png')

def plot_ants(all_lengths, all_best):
    plt.figure(figsize=(5, 5), dpi=500)
    plt.plot(all_lengths, 'g.')
    plt.plot(all_best, 'r-', label='history_best')
    plt.xlabel('Iteration')
    plt.ylabel('length')
    plt.legend()
    plt.savefig('ants.png')
    plt.show()
    plt.close()

def find_fittest(routes_length, pop_size):
    key = 10000000000
    fittest = 0
    for i in range(pop_size):
        if routes_length[i] < key:
            key = routes_length[i]
            fittest = i
    return fittest

def initiate(ant_number, city_num):
    ant_site = [0] * ant_number
    for i in range(ant_number):
        ant_site[i] = np.random.randint(0, city_num)

    return ant_site

def roulette_wheel_selection(city_number, select):
    sum_p = sum(select)
    index = 0
    for i in range(city_number):
        select[i] = select[i] / sum_p
    selected = random.random()
    while select[index] < selected:
        select[index + 1] += select[index]
        index += 1

    return index

def create_route(city_num, P, ant_site):
    select = P.copy()
    index = ant_site
    ant_route = [0] * city_num
    ant_route[0] = ant_site
    for i in range(city_num):
        select[i][ant_site] = 0
    for i in range(city_num - 1):
        index = roulette_wheel_selection(city_num, select[index])
        ant_route[i + 1] = index
        for j in range(city_num):
            select[j][index] = 0

    return ant_route


def update(city_num, ants_site, a, b, p, q, pheromone, distances, ant_number):
    P = np.zeros([city_num, city_num])
    for i in range(city_num):
        for j in range(city_num):
            if i != j:
                P[i][j] = pheromone[i][j] ** a * (1 / distances[i][j]) ** b

    """**********创建路径***********"""
    ants_route = [0] * ant_number
    for i in range(city_num):
        ants_route[i] = [0] * city_num
    ants_length = [0] * ant_number
    for i in range(ant_number):
        ants_route[i] = create_route(city_num, P, ants_site[i])
        for j in range(city_num - 1):
            ants_length[i] += distances[ants_route[i][j]][ants_route[i][j + 1]]
        ants_length[i] += distances[ants_route[i][0]][ants_route[i][city_num - 1]]

    """***********更新信息浓度************"""
    pheromone_add = np.zeros([city_num, city_num])
    for i in range(ant_number):
        for j in range(city_num - 1):
            pheromone_add[ants_route[i][j]][ants_route[i][j + 1]] += q / ants_length[i]

    for i in range(city_num):
        for j in range(city_num):
            pheromone[i][j] = (1 - p) * pheromone[i][j] + pheromone_add[i][j]

    return pheromone, ants_length, ants_route


def ACO(city_num, distances):
    ant_number = int(city_num * 1.5)
    pheromone = np.ones([city_num, city_num])
    q = 500            # 信息素常量
    max_t = 30       # 迭代次数
    a = 2              # 信息素因子
    b = 3              # 启发因子
    p = 0.1            # 信息素挥发因子
    hope_value = 400
    best_route = [0] * city_num
    best_length = 10000000000

    all_lengths = []
    all_best = np.zeros(max_t)

    for i in range(max_t):
        ants_site = initiate(ant_number, city_num)
        pheromone, ants_lengths, ants_route = update(city_num, ants_site, a, b, p, q,
                                                     pheromone, distances, ant_number)

        index = find_fittest(ants_lengths, ant_number)
        if ants_lengths[index] < best_length:
            best_length = ants_lengths[index]
            best_route = ants_route[index]
            if best_length < hope_value:
                break

        all_lengths.append(ants_lengths)
        all_best[i] = best_length

    return best_length, best_route, all_lengths, all_best




def main():
    city_num = 30
    cities = gen_cities(city_num, random_state=True)
    distances = get_distance_mateix(cities)
    best_length, best_route, all_lengths, all_best = ACO(city_num, distances)
    print("Best path is:", best_route, "with length", best_length, '\n')
    plot_map(cities, best_route)
    plot_ants(all_lengths, all_best)
    print(all_best)


if __name__=="__main__":
    main()
    plt.show()

运行结果如下：

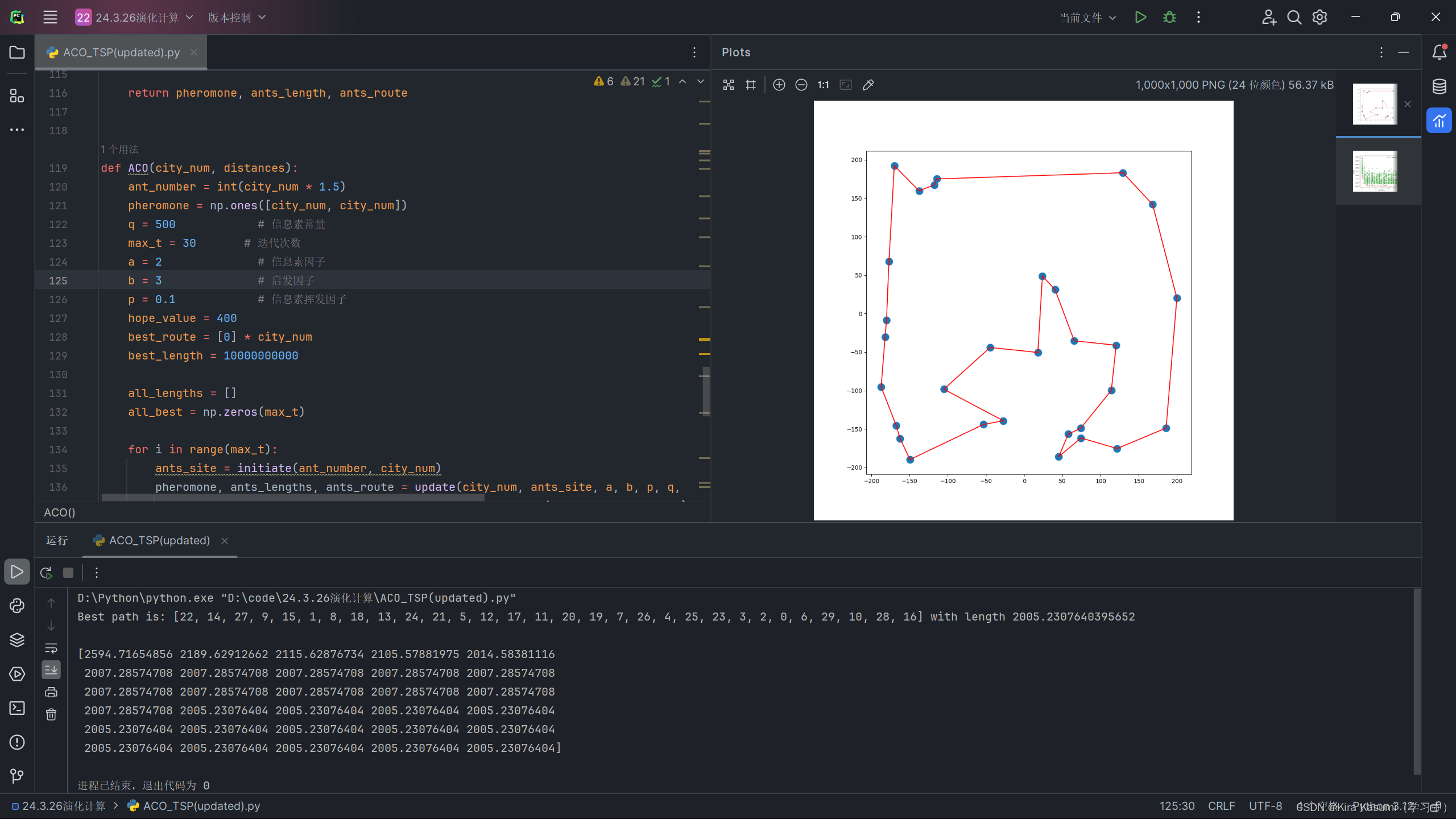
这里30个城市的情况下迭代15次左右就已经是最优解了，实际还能再压缩蚁群的迭代次数。