SURF算法及原理

没有不重的名么

已于 2025-01-13 15:21:31 修改

阅读量1.1k

点赞数 37

分类专栏：深度学习文章标签：算法计算机视觉人工智能目标跟踪

于 2024-12-18 16:14:25 首次发布

本文链接：https://blog.csdn.net/m0_61595251/article/details/144552488

版权

深度学习专栏收录该内容

15 篇文章

订阅专栏

SURF算法与源码分析、上 - ☆Ronny丶 - 博客园

SURF算法与源码分析、下 - ☆Ronny丶 - 博客园

【CV学习5】SURF算法详解 - 苟富贵 - 博客园

与SIFT的区别：

①SIFT在构造DOG金字塔以及求DOG局部空间极值比较耗时，SURF的改进是使用Hessian矩阵变换图像，极值的检测只需计算Hessian矩阵行列式，作为进一步优化，使用一个简单的方程可以求出Hessian行列式近似值，使用盒状模糊滤波（box blur）求高斯模糊近似值。

②SURF不使用降采样，通过保持图像大小不变，但改变盒状滤波器的大小来构建尺度金字塔。

③在计算关键点主方向以及关键点周边像素方向的方法上，SURF不使用直方图统计，而是使用哈尔(haar)小波转换。SIFT的KPD达到128维，导致KPD的比较耗时，SURF使用哈尔(haar)小波转换得到的方向，让SURF的KPD降到64维，减少了一半，提高了匹配速度

SURF借鉴了SIFT中简化近似的思想，把DoH中的高斯二阶微分模板进行了简化，使得模板对图像的滤波只需要进行几个简单的加减法运算，并且，这种运算与滤波器的尺度无关。

实验证明，SURF算法较SIFT在运算速度上要快3倍左右。

SURF：

积分图像：

SURF中使用积分图像的概念，借助积分图像，图像与高斯二阶微分模板的滤波转化为对积分图像的加减运算

积分图像中任意一点 $(i,j)$ 的值 $ii(i,j)$ 为原图像左上角到点 $(i,j)$ 相应的对角线区域灰度值总和：

$ii(i,j)=\sum_{r\leqslant i,c\leqslant j}^{}p(r,c)$

$p(r,c)$ 表示图像中点 $(r,c)$ 的灰度值， $ii(i,j)$ 使用迭代运算得到：

$S(i,j)=S(i,j-1)+p(i,j)$

$ii(i,j)=ii(i-1,j)+S(i,j)$

$S(i,j)$ 表示一列的积分，且 $S(i,-1)=0,ii(i,j)=0$ ，求积分图像，只需要对原图像所有像素进行一遍扫描

OpenCV中提供接口：

# src :输入图像，大小为M*N
# **** sum: 输出的积分图像，大小为（M+1）*（N+1）****
# sdepth：用于指定sum的类型，-1表示与src类型一致
void integral(InputArray src, OutputArray sum, int sdepth = -1);

OpenCV中积分图使用的计算公式为：

$ii(i,j)=\sum_{r<i,c<j}^{}p(r,c)$

因此它输出的大小是(M+1)*(N+1)

积分图像与原始图像的关系：

积分图像与原始图像的尺寸相同，积分图像中每个位置坐标与原始灰度图像的像素坐标相对应。

不同的是，在原始图像采用灰度图像的情况下，灰度图像每个像素使用8bit表示，而积分图像由于像素的累加运算，或图像尺度的变化，积分图像中每个像素位宽将会需要积分的像素尾款来表示

构建：

对于一幅原始的灰度图像，以图像中的第一个像素位置作为坐标原点，向右为 $x$ 轴正向，向下为
$y$ 轴正向建立坐标系

将任意像素 $(x,y)$ 与坐标原点之间围成的矩形区域内所有像素值相加得到一个新的值，定义为积分像素值。

构建好积分图后，任意矩形内的像素累加只需要使用矩形四个顶角位置的积分像素值进行加减运算即可得到：

代码：

该函数接受一个积分图像，以及尺寸相关的参数，组数与每组的层数，检测到的特征点保存在vector<KeyPoint>类型的结构中。

static void fastHessianDetector(const Mat& sum, const Mat& msum, vector<KeyPoint>& keypoints,
    int nOctaves, int nOctaveLayers, float hessianThreshold)
{
    # first Octave图像采样的步长，第二组的时候加倍，以此内推增加这个值，将会加快特征点检测的速度，但是会让特征点的提取变得不稳定
    const int SAMPLE_STEP0 = 1;

    int nTotalLayers = (nOctaveLayers + 2)*nOctaves; # 尺度空间的总图像数
    int nMiddleLayers = nOctaveLayers*nOctaves; # 用于检测特征点的层的 总数，也就是中间层的总数

    vector<Mat> dets(nTotalLayers); # 每一层图像 对应的 Hessian行列式的值
    vector<Mat> traces(nTotalLayers); # 每一层图像 对应的 Hessian矩阵的迹的值
    vector<int> sizes(nTotalLayers); # 每一层用的 Harr模板的大小
    vector<int> sampleSteps(nTotalLayers); # 每一层用的采样步长 
    vector<int> middleIndices(nMiddleLayers); # 中间层的索引值

    keypoints.clear();

    # 为上面的对象分配空间，并赋予合适的值
    int index = 0, middleIndex = 0, step = SAMPLE_STEP0;

    for (int octave = 0; octave < nOctaves; octave++)
    {
        for (int layer = 0; layer < nOctaveLayers + 2; layer++)
        {
            # 这里sum.rows - 1是因为 sum是积分图，它的大小是原图像大小加1
            # 这里面有除以遍历图像用的步长
            dets[index].create((sum.rows - 1) / step, (sum.cols - 1) / step, CV_32F); 
            traces[index].create((sum.rows - 1) / step, (sum.cols - 1) / step, CV_32F);
            sizes[index] = (SURF_HAAR_SIZE0 + SURF_HAAR_SIZE_INC*layer) << octave;
            sampleSteps[index] = step;

            if (0 < layer && layer <= nOctaveLayers)
                middleIndices[middleIndex++] = index;
            index++;
        }
        step *= 2;
    }
    # Calculate hessian determinant and trace samples in each layer
    for (int i = 0; i < nTotalLayers; i++)
    {
        calcLayerDetAndTrace(sum, sizes[i], sampleSteps[i], dets[i], traces[i]);
    }

    # Find maxima in the determinant of the hessian
    for (int i = 0; i < nMiddleLayers; i++)
    {
        int layer = middleIndices[i];
        int octave = i / nOctaveLayers;
        findMaximaInLayer(sum, msum, dets, traces, sizes, keypoints, octave, layer, hessianThreshold, sampleSteps[layer]);
    }

    std::sort(keypoints.begin(), keypoints.end(), KeypointGreater());

DoH近似：

Hessian矩阵：

目的：生成图像稳定的边缘点（突变点），为后续特征提取做准备

在SURF算法中，图像像素 $I(x,y)$ 即为函数值 $f(x,y)$ 。但由于特征点需要具备尺度无关性，所以在进行Hessian矩阵构造前，需要对其进行高斯滤波，选用二阶标准高斯函数作为滤波器:

给定图像 $I$ 中的一个点 $x(i,j)$ ，在 $x$ 处，尺度为 $\sigma$ 的Hessian矩阵 $H(x,\sigma )$ 定义如下：

$L_{xx}(x,\sigma )\; \: \: \: \: L_{xy}(x,\sigma )$

$H(x,\sigma )=\left [ L_{xx}(x,\sigma )\; \: \: \: \: L_{xy}(x,\sigma )\right ]$

二阶形式如下：

$L_{xx}(x,\sigma )$ 为高斯二阶微分 $\frac{\alpha ^{2}g(\sigma)}{\alpha x^{2}}$ 在 $x$ 处与图像 $I$ 的卷积， $L_{xy}$ 等同理

Hessian矩阵的形式：

SIFT中使用高斯差分对 $L_{xx}$ 、 $L_{xy}$ 、 $L_{yy}$ 进行近似估计，使用 $D_{xx}$ 、 $D_{xy}$ 、 $D_{yy}$ 代替高斯拉普拉斯函数：

$D(x,y,\sigma )=(G(x,y,k\sigma )-G(x,y,\sigma ))*I(x,y)$

$=L(x,y,k\sigma )-L(x,y,\sigma )$

当Hessian矩阵的判别式取得局部极大值时，判定当前点是比周围邻域内其他点更亮或更暗的点，由此来定位关键点的位置，Hessian矩阵的判别式为：

三种高斯微分算子的图形如下：

代码：

这个函数首先定义了尺寸为9的第一层图像的三个模板。模板分别为一个3×5、3×5、4×5的二维数组表示，数组的每一行表示一个黑白块的位置参数。函数里只初始化了第一层图像的模板参数，后面其他组其他层的Harr模板参数都是用resizeHaarPattern这个函数来计算的。

struct SurfHF
{
    int p0, p1, p2, p3;
    float w;

    # 返回的是一个SurfHF的结构体，由两个点及一个权重构成。 
    SurfHF() : p0(0), p1(0), p2(0), p3(0), w(0) {}
};

resizeHaarPattern把模板中的点坐标转换到在积分图中的相对（模板左上角点）坐标。

static void
resizeHaarPattern(const int src[][5], SurfHF* dst, int n, int oldSize, int newSize, int widthStep)
{
    float ratio = (float)newSize / oldSize;
    for (int k = 0; k < n; k++)
    {
        int dx1 = cvRound(ratio*src[k][0]);
        int dy1 = cvRound(ratio*src[k][1]);
        int dx2 = cvRound(ratio*src[k][2]);
        int dy2 = cvRound(ratio*src[k][3]);
        # 巧妙的坐标转换
        # 换为一个相对距离，距离模板左上角点的在积分图中的距离
        dst[k].p0 = dy1*widthStep + dx1;
        dst[k].p1 = dy2*widthStep + dx1; 
        dst[k].p2 = dy1*widthStep + dx2;
        dst[k].p3 = dy2*widthStep + dx2;
        # 原来的+1,+2用 覆盖的所有像素点平均。
        dst[k].w = src[k][4] / ((float)(dx2 - dx1)*(dy2 - dy1));
    }
}

在用积分图计算近似卷积时，使用calcHaarPattern函数

inline float calcHaarPattern(const int* origin, const SurfHF* f, int n)
{
    # orgin即为积分图，n为模板中黑白块的个数
    double d = 0;
    for (int k = 0; k < n; k++)
        d += (origin[f[k].p0] + origin[f[k].p3] - origin[f[k].p1] - origin[f[k].p2])*f[k].w;
    return (float)d;
}

整个calcLayerDetAndTrack的代码

static void calcLayerDetAndTrace(const Mat& sum, int size, int sampleStep,
    Mat& det, Mat& trace)
{
    const int NX = 3, NY = 3, NXY = 4;
    const int dx_s[NX][5] = { { 0, 2, 3, 7, 1 }, { 3, 2, 6, 7, -2 }, { 6, 2, 9, 7, 1 } };
    const int dy_s[NY][5] = { { 2, 0, 7, 3, 1 }, { 2, 3, 7, 6, -2 }, { 2, 6, 7, 9, 1 } };
    const int dxy_s[NXY][5] = { { 1, 1, 4, 4, 1 }, { 5, 1, 8, 4, -1 }, { 1, 5, 4, 8, -1 }, { 5, 5, 8, 8, 1 } };

    SurfHF Dx[NX], Dy[NY], Dxy[NXY];

    if (size > sum.rows - 1 || size > sum.cols - 1)
        return;
    resizeHaarPattern(dx_s, Dx, NX, 9, size, sum.cols);
    resizeHaarPattern(dy_s, Dy, NY, 9, size, sum.cols);
    resizeHaarPattern(dxy_s, Dxy, NXY, 9, size, sum.cols);

    # The integral image 'sum' is one pixel bigger than the source image 
    # 最大能遍历到的行坐标，因为要减掉一个模板的尺寸
    int samples_i = 1 + (sum.rows - 1 - size) / sampleStep; 
    # 最大能遍历到的列坐标
    int samples_j = 1 + (sum.cols - 1 - size) / sampleStep;  

    # Ignore pixels where some of the kernel is outside the image 
    int margin = (size / 2) / sampleStep;

    for (int i = 0; i < samples_i; i++)
    {
        # 坐标为(i,j)的点是模板左上角的点，所以实际现在模板分析是的i+margin,j+margin点处的响应
        const int* sum_ptr = sum.ptr<int>(i*sampleStep);
        float* det_ptr = &det.at<float>(i + margin, margin); // 左边空隙为 margin
        float* trace_ptr = &trace.at<float>(i + margin, margin);
        for (int j = 0; j < samples_j; j++)
        {
            float dx = calcHaarPattern(sum_ptr, Dx, 3);
            float dy = calcHaarPattern(sum_ptr, Dy, 3);
            float dxy = calcHaarPattern(sum_ptr, Dxy, 4);
            sum_ptr += sampleStep;
            det_ptr[j] = dx*dy - 0.81f*dxy*dxy;
            trace_ptr[j] = dx + dy;
        }
    }
}

interpolateKeypoint函数通过插值计算最大值点

static int
interpolateKeypoint(float N9[3][9], int dx, int dy, int ds, KeyPoint& kpt)
{
    Vec3f b(-(N9[1][5] - N9[1][3]) / 2,  // Negative 1st deriv with respect to x
        -(N9[1][7] - N9[1][1]) / 2,  // Negative 1st deriv with respect to y
        -(N9[2][4] - N9[0][4]) / 2); // Negative 1st deriv with respect to s

    Matx33f A(
        N9[1][3] - 2 * N9[1][4] + N9[1][5],            // 2nd deriv x, x
        (N9[1][8] - N9[1][6] - N9[1][2] + N9[1][0]) / 4, // 2nd deriv x, y
        (N9[2][5] - N9[2][3] - N9[0][5] + N9[0][3]) / 4, // 2nd deriv x, s
        (N9[1][8] - N9[1][6] - N9[1][2] + N9[1][0]) / 4, // 2nd deriv x, y
        N9[1][1] - 2 * N9[1][4] + N9[1][7],            // 2nd deriv y, y
        (N9[2][7] - N9[2][1] - N9[0][7] + N9[0][1]) / 4, // 2nd deriv y, s
        (N9[2][5] - N9[2][3] - N9[0][5] + N9[0][3]) / 4, // 2nd deriv x, s
        (N9[2][7] - N9[2][1] - N9[0][7] + N9[0][1]) / 4, // 2nd deriv y, s
        N9[0][4] - 2 * N9[1][4] + N9[2][4]);           // 2nd deriv s, s

    Vec3f x = A.solve(b, DECOMP_LU);

    bool ok = (x[0] != 0 || x[1] != 0 || x[2] != 0) &&
        std::abs(x[0]) <= 1 && std::abs(x[1]) <= 1 && std::abs(x[2]) <= 1;

    if (ok)
    {
        kpt.pt.x += x[0] * dx;
        kpt.pt.y += x[1] * dy;
        kpt.size = (float)cvRound(kpt.size + x[2] * ds);
    }
    return ok;
}

static void findMaximaInLayer(const Mat& sum, const Mat& mask_sum,
    const vector<Mat>& dets, const vector<Mat>& traces,
    const vector<int>& sizes, vector<KeyPoint>& keypoints,
    int octave, int layer, float hessianThreshold, int sampleStep)
{
    // Wavelet Data
    const int NM = 1;
    const int dm[NM][5] = { { 0, 0, 9, 9, 1 } };
    SurfHF Dm;

    int size = sizes[layer];

    # 当前层图像的大小
    int layer_rows = (sum.rows - 1) / sampleStep;
    int layer_cols = (sum.cols - 1) / sampleStep;

    # 边界区域大小，考虑的下一层的模板大小
    int margin = (sizes[layer + 1] / 2) / sampleStep + 1;

    if (!mask_sum.empty())
        resizeHaarPattern(dm, &Dm, NM, 9, size, mask_sum.cols);

    int step = (int)(dets[layer].step / dets[layer].elemSize());

    for (int i = margin; i < layer_rows - margin; i++)
    {
        const float* det_ptr = dets[layer].ptr<float>(i);
        const float* trace_ptr = traces[layer].ptr<float>(i);
        for (int j = margin; j < layer_cols - margin; j++)
        {
            float val0 = det_ptr[j]; // 中心点的值
            if (val0 > hessianThreshold)
            {
                # 模板左上角的坐标
                int sum_i = sampleStep*(i - (size / 2) / sampleStep);
                int sum_j = sampleStep*(j - (size / 2) / sampleStep);


                const float *det1 = &dets[layer - 1].at<float>(i, j);
                const float *det2 = &dets[layer].at<float>(i, j);
                const float *det3 = &dets[layer + 1].at<float>(i, j);
                float N9[3][9] = { { det1[-step - 1], det1[-step], det1[-step + 1],
                    det1[-1], det1[0], det1[1],
                    det1[step - 1], det1[step], det1[step + 1] },
                    { det2[-step - 1], det2[-step], det2[-step + 1],
                    det2[-1], det2[0], det2[1],
                    det2[step - 1], det2[step], det2[step + 1] },
                    { det3[-step - 1], det3[-step], det3[-step + 1],
                    det3[-1], det3[0], det3[1],
                    det3[step - 1], det3[step], det3[step + 1] } };


                if (!mask_sum.empty())
                {
                    const int* mask_ptr = &mask_sum.at<int>(sum_i, sum_j);
                    float mval = calcHaarPattern(mask_ptr, &Dm, 1);
                    if (mval < 0.5)
                        continue;
                }

                # 检测val0，是否在N9里极大值，？？为什么不检测极小值呢*/
                if (val0 > N9[0][0] && val0 > N9[0][1] && val0 > N9[0][2] &&
                    val0 > N9[0][3] && val0 > N9[0][4] && val0 > N9[0][5] &&
                    val0 > N9[0][6] && val0 > N9[0][7] && val0 > N9[0][8] &&
                    val0 > N9[1][0] && val0 > N9[1][1] && val0 > N9[1][2] &&
                    val0 > N9[1][3] && val0 > N9[1][5] &&
                    val0 > N9[1][6] && val0 > N9[1][7] && val0 > N9[1][8] &&
                    val0 > N9[2][0] && val0 > N9[2][1] && val0 > N9[2][2] &&
                    val0 > N9[2][3] && val0 > N9[2][4] && val0 > N9[2][5] &&
                    val0 > N9[2][6] && val0 > N9[2][7] && val0 > N9[2][8])
                {
                    # Calculate the wavelet center coordinates for the maxima 
                    float center_i = sum_i + (size - 1)*0.5f;
                    float center_j = sum_j + (size - 1)*0.5f;

                    KeyPoint kpt(center_j, center_i, (float)sizes[layer],
                        -1, val0, octave, CV_SIGN(trace_ptr[j]));

                    # 局部极大值插值，用Hessian，类似于SIFT里的插值，里面没有迭代5次，只进行了一次查找，why?  
                    int ds = size - sizes[layer - 1];
                    int interp_ok = interpolateKeypoint(N9, sampleStep, sampleStep, ds, kpt);

                    # Sometimes the interpolation step gives a negative size etc. 
                    if (interp_ok)
                    {
                        /*printf( "KeyPoint %f %f %d\n", point.pt.x, point.pt.y, point.size );*/
                        keypoints.push_back(kpt);
                    }
                }
            }
        }
    }
}

盒式滤波器：

高斯核服从正态分布，从中心点向外，系数越来越低，为了提高运算速度，Surf采用盒式滤波器来近似代替高斯滤波器，以提高运算速度。

盒式滤波器（Boxfilter）对图像的滤波转化成计算图像上不同区域间像素和的加减运算问题，只需要简单几次查找积分图就可以完成。每个像素的Hessian矩阵行列式的近似值：

在 $D_{xy}$ 上乘了一个加权系数0.9，目的是为了平衡因使用盒式滤波器近似所带来的误差。

为了将模板与图像的卷积转换为盒式滤波运算，需要对高斯二阶微分模板进行简化，使得简化后的模板只是由几个矩形区域组成，矩形区域内填充同一值，如下图所示，在简化模板中白色区域的值为正数，黑色区域的值为负数，灰度区域的值为0：

对于σ=1.2的高斯二阶微分滤波器，设定模板的尺寸为9×9的大小，并用它作为最小尺度空间值对图像进行滤波和斑点检测。使用 $D_{xx}$ 、 $D_{xy}$ 和 $D_{yy}$ 表示模板与图像进行卷积的结果，将Hessian矩阵的行列式作如下的简化：

为保持高斯核与近似高斯核一致性，平衡Hessian行列式表示式，使用滤波器响应的相关权重 $w$ ：

使用不同的模板尺寸，就形成了多尺度斑点响应的金字塔图像

尺度空间表示：

对比：

一般通过不同 $\sigma$ 的高斯函数，对图像进行平滑滤波，然后重采样图像获得更高一层的金字塔图像。

SIFT：通过相邻两层图像金字塔相减得到DoG图像，然后在DoG图像上进行斑点和边缘检测工作

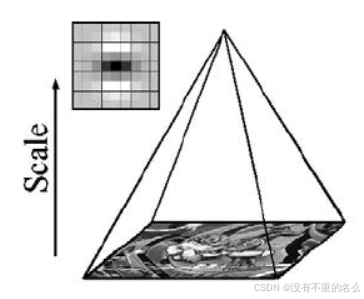
图像金字塔分为若干组（Octave），同时每组又有若干层（Layer）图片组成

SURF：通过不同尺寸盒子滤波模板与积分图像求取Hessian矩阵行列式的响应图像，然后在响应图像上采用3D非极大值抑制，求取各种不同尺度的斑点。

过程：

①将尺度空间划分为若干组，一个组代表了逐步放大的滤波模板对同一输入图像进行滤波的一系列响应图，每个组又由若干固定的层组成，两个层之间的最小尺度变化量是盒子滤波器模板尺寸的1/3。

对于9×9的模板， $l_{0}$ =3。下一层的响应长度至少应该在 $l_{0}$ 的基础上增加2个像素，以保证一边一个像素，即 $l_{0}$ =5。

黑色、白色区域的长度增加偶数个像素，以保证一个中心像素的存在

②将滤波器尺寸增加量翻倍（6，12，24，38）。这样，可以得到第二组的滤波器尺寸

第三组的滤波器尺寸为27，51，75，99。如果原始图像的尺寸仍然大于对应的滤波器尺寸，尺度空间的分析还可以进行第四组，其对应的模板尺寸分别为51，99，147和195。

下图显示了第一组至第三组的滤波器尺寸变化。

对于尺寸为L的模板，当用它与积分图运算来近似二维高斯核的滤波时，对应的二维高斯核的参数σ=1.2×(L/9)，这一点至关重要，尤其是在后面计算描述子时，用于计算邻域的半径时。

Hessian行列式图像的产生过程：

在SURF算法的尺度空间中，每一组中任意一层包括 $D_{xx},D_{yy},D_{xy}$ 三种盒子滤波器

对一幅输入图像进行滤波后通过Hessian行列式计算公式可以得到对于尺度坐标下的Hessian行列式的值，所有Hessian行列式值构成一幅Hessian行列式图像

兴趣点的定位：

为在图像及不同尺寸中定位兴趣点，使用3×3×3邻域非最大值抑制。具体的步骤基本与SIFT一致，而且Hessian矩阵行列式的最大值在尺度和图像空间被插值。

用积分图来简化卷积，用不同的模板来近似原来尺度空间中的高斯滤波器。

SURF特征点方向分配：

为保证特征矢量具有旋转不变性，需要对每个特征点分配一个主方向

以特征点为中心，以6*s（s=1.2∗L/9为特征点的尺度）为半径的圆形区域，对图像进行Haar小波响应运算。实际就是对图像进行梯度运算，只不过需利用积分图像，提高计算图像梯度的效率。

考虑到Haar小波的模板带宽，实际计算梯度的图像区域与SIFT求取特征点主方向的区域是相同的，用于计算梯度的Harr小波的尺度为4s。

左侧模板计算x方向的响应，右侧模板计算y方向的响应，黑色表示-1，白色表示+1。

与SIFT类似，使用 $\sigma =2s$ 的高斯加权函数对Harr小波的响应值进行高斯加权。为了求取主方向值，需要设计一个以特征点为中心，张角为 $\frac{\pi }{3}$ 的扇形滑动窗口。以步长为0.2弧度左右，旋转这个滑动窗口，并对滑动窗口内的图像Harr小波响应值 $dx,dy$ 进行累加，得到一个矢量 $(mw,\theta w)$ :

主方向为最大Harr响应累加值所对应的方向，也就是最长矢量所对应的方向，即

按照SIFT求方向时策略，当存在另一个相当于主峰值80%能量的峰值时，则将这个方向认为是该特征点的辅方向。

一个特征点可能会被指定有多个方向（一个主方向，一个以上辅方向），以增强匹配的鲁棒性

与SIFT的描述子类似，如果在 $m_{w}$ 中出现另一个大于主峰能量 $max[m_{w}]$ 的80%时的次峰，可以将该特征点复制成两个特征点。一个主的方向为最大响应能量所对应的方向，另一个主方向为次大响应能量所对应的方向。

特征点特征矢量生成：

SURF中，在关键点周围选取一个正方形框，方向为关键点的主方向，边长为20S。将其划分为16个区域（边长为5S），每个区域统计25个像素的水平方向和垂直方向的Haar小波特性（均相对于正方形框的主方向确定的）

生成特征点描述子，需要在一个矩形区域来计算Haar小波响应。

以特征点为中心，沿主方向将20s×20s的图像划分为4×4个子块，每个子块利用尺寸2s的Harr模板进行响应值计算，然后对响应值进行统计 $\sum dx,\sum \left | dx \right |,\sum dy,\sum \left | dy \right |$ 形成特征矢量。

图中以特征点为中心，以20s为边长的矩形窗口为特征描述子计算使用的窗口，特征点到矩形边框的线段表示特征点的主方向。

将20s的窗口划分成4×4子窗口，每个子窗口有5s×5s个像素。使用尺寸为2s的Harr小波对子窗口图像进行其响应值计算，共进行25次采样，分别得到沿主方向的 $dy$ 和垂直于主方向的 $dx$ 。然后，以特征点为中心，对 $dy$ 和 $dx$ 进行高斯加权计算，高斯核的参数为σ=3.3s(即20s/6)。最后分别对每个子块的响应值进行统计，得到每个子块的矢量：

由于共有4×4个子块，因此，特征描述子共由4×4×4=64维特征矢量组成。

SURF描述子不仅具有尺度和旋转不变性，而且对光照的变化也具有不变性。使小波响应本身就具有亮度不变性，而对比度的不变性则是通过将特征矢量进行归一化来实现。

对于实际图像的描述子，认为它们是由这三种不同模式图像的描述子组合而成的。

为了充分利用积分图像进行Haar小波的响应计算，并不直接旋转Haar小波模板求得其响应值，而是在积图像上先使用水平和垂直的Haar模板求得响应值 $dy$ 和 $dx$ ，然后根据主方向旋转 $dx$ 和 $dy$ 与主方向操持一致。

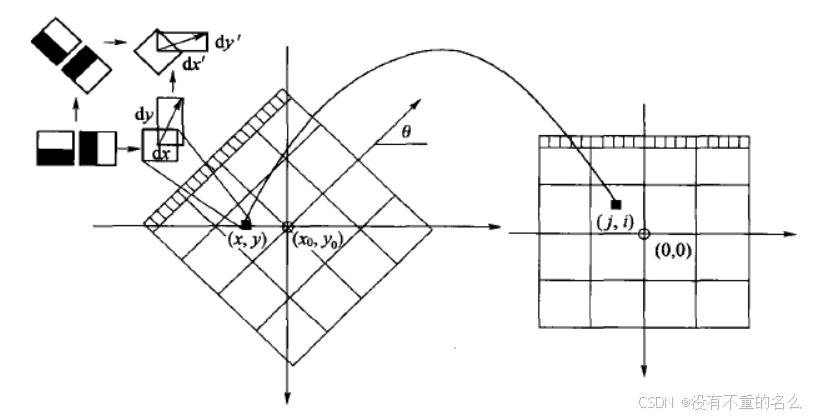
为了求得旋转后Haar小波响应值，首先要得到旋转前图像的位置。旋转前后图偈的位置关系，可以通过点的旋转公式得到：

在得到点 $(j,i)$ 在旋转前对应积分图像的位置 $(x,y)$ 后，利用积分图像与水平、垂直Harr小波，求得水平与垂直两个方向的响应值 $dx$ 和 $dy$ 。对dx和dy进行高斯加权处理，并根据主方向的角度，对 $dx$ 和 $dy$ 进行旋转变换，从而，得到旋转后的 $dx{}'$ ’和 $dy{}'$ 。其计算公式如下：

代码：

通过SURFInvoker这个类来实现。在主流程中，通过一个parallel_for_()函数来并发计算。

struct SURFInvoker
{
    enum{ORI_RADIUS = 6, ORI_WIN = 60, PATCH_SZ = 20};
    // Parameters
    const Mat* img;
    const Mat* sum;
    vector<KeyPoint>* keypoints;
    Mat* descriptors;
    bool extended;
    bool upright;

    // Pre-calculated values
    int nOriSamples;
    vector<Point> apt; // 特征点周围用于描述方向的邻域的点
    vector<float> aptw; // 描述 方向时的 高斯 权
    vector<float> DW;


    SURFInvoker(const Mat& _img, const Mat& _sum,
        vector<KeyPoint>& _keypoints, Mat& _descriptors,
        bool _extended, bool _upright)
    {
        keypoints = &_keypoints;
        descriptors = &_descriptors;
        img = &_img;
        sum = &_sum;
        extended = _extended;
        upright = _upright;

        # 用于描述特征点的 方向的 邻域大小： 12*sigma+1 (sigma =1.2) 因为高斯加权的核的参数为2sigma
        # nOriSampleBound为 矩形框内点的个数
        const int nOriSampleBound = (2 * ORI_RADIUS + 1)*(2 * ORI_RADIUS + 1); // 这里把s近似为1 ORI_DADIUS = 6s

        # 分配大小 
        apt.resize(nOriSampleBound);
        aptw.resize(nOriSampleBound);
        DW.resize(PATCH_SZ*PATCH_SZ); // PATHC_SZ为特征描述子的 区域大小 20s(s 这里初始为1了)

        # 计算特征点方向用的高斯分布权值与坐标
        Mat G_ori = getGaussianKernel(2 * ORI_RADIUS + 1, SURF_ORI_SIGMA, CV_32F); // SURF_ORI_SIGMA = 1.2 *2 =2.5
        nOriSamples = 0;
        for (int i = -ORI_RADIUS; i <= ORI_RADIUS; i++)
        {
            for (int j = -ORI_RADIUS; j <= ORI_RADIUS; j++)
            {
                if (i*i + j*j <= ORI_RADIUS*ORI_RADIUS) // 限制在圆形区域内
                {
                    apt[nOriSamples] = cvPoint(i, j);
                    # 下面这里有个坐标转换，因为i,j都是从-ORI_RADIUS开始的。
                    aptw[nOriSamples++] = G_ori.at<float>(i + ORI_RADIUS, 0) * G_ori.at<float>(j + ORI_RADIUS, 0);
                }
            }
        }
        # nOriSamples为圆形区域内的点，nOriSampleBound是正方形区域的点
        CV_Assert(nOriSamples <= nOriSampleBound); 

        # 用于特征点描述子的高斯权值 
        Mat G_desc = getGaussianKernel(PATCH_SZ, SURF_DESC_SIGMA, CV_32F); # 用于生成特征描述子的高斯加权 sigma = 3.3s (s初取1)
        for (int i = 0; i < PATCH_SZ; i++)
        {
            for (int j = 0; j < PATCH_SZ; j++)
                DW[i*PATCH_SZ + j] = G_desc.at<float>(i, 0) * G_desc.at<float>(j, 0);
        }

        # x与y方向上的 Harr小波,参数为4s 
        const int NX = 2, NY = 2;
        const int dx_s[NX][5] = { { 0, 0, 2, 4, -1 }, { 2, 0, 4, 4, 1 } };
        const int dy_s[NY][5] = { { 0, 0, 4, 2, 1 }, { 0, 2, 4, 4, -1 } };

        float X[nOriSampleBound], Y[nOriSampleBound], angle[nOriSampleBound]; # 用于计算特生点主方向
        uchar PATCH[PATCH_SZ + 1][PATCH_SZ + 1];
        float DX[PATCH_SZ][PATCH_SZ], DY[PATCH_SZ][PATCH_SZ]; # 20s * 20s区域的 梯度值
        CvMat matX = cvMat(1, nOriSampleBound, CV_32F, X);
        CvMat matY = cvMat(1, nOriSampleBound, CV_32F, Y);
        CvMat _angle = cvMat(1, nOriSampleBound, CV_32F, angle);
        Mat _patch(PATCH_SZ + 1, PATCH_SZ + 1, CV_8U, PATCH);

        int dsize = extended ? 128 : 64;

        int k, k1 = 0, k2 = (int)(*keypoints).size();// k2为Harr小波的 模板尺寸
        float maxSize = 0;
        for (k = k1; k < k2; k++)
        {
            maxSize = std::max(maxSize, (*keypoints)[k].size);
        }
        # maxSize*1.2/9 表示最大的尺度 s
        int imaxSize = std::max(cvCeil((PATCH_SZ + 1)*maxSize*1.2f / 9.0f), 1);
        Ptr<CvMat> winbuf = cvCreateMat(1, imaxSize*imaxSize, CV_8U);
        for (k = k1; k < k2; k++)
        {
            int i, j, kk, nangle;
            float* vec;
            SurfHF dx_t[NX], dy_t[NY];
            KeyPoint& kp = (*keypoints)[k];
            float size = kp.size;
            Point2f center = kp.pt;
            # s是当前层的尺度参数 1.2是第一层的参数，9是第一层的模板大小
            float s = size*1.2f / 9.0f;
            # grad_wav_size是 harr梯度模板的大小边长为4s 
            int grad_wav_size = 2 * cvRound(2 * s);
            if (sum->rows < grad_wav_size || sum->cols < grad_wav_size)
            {
                kp.size = -1;
                continue;
            }

            float descriptor_dir = 360.f - 90.f;
            if (upright == 0)
            {
                # 这一步 是计算梯度值，先将harr模板放大，再根据积分图计算，与前面求D_x，D_y一致类似
                resizeHaarPattern(dx_s, dx_t, NX, 4, grad_wav_size, sum->cols);
                resizeHaarPattern(dy_s, dy_t, NY, 4, grad_wav_size, sum->cols);
                for (kk = 0, nangle = 0; kk < nOriSamples; kk++)
                {
                    int x = cvRound(center.x + apt[kk].x*s - (float)(grad_wav_size - 1) / 2);
                    int y = cvRound(center.y + apt[kk].y*s - (float)(grad_wav_size - 1) / 2);
                    if (y < 0 || y >= sum->rows - grad_wav_size ||
                        x < 0 || x >= sum->cols - grad_wav_size)
                        continue;
                    const int* ptr = &sum->at<int>(y, x);
                    float vx = calcHaarPattern(ptr, dx_t, 2);
                    float vy = calcHaarPattern(ptr, dy_t, 2);
                    X[nangle] = vx*aptw[kk];
                    Y[nangle] = vy*aptw[kk];
                    nangle++;
                }
                if (nangle == 0)
                {

                    kp.size = -1;
                    continue;
                }
                matX.cols = matY.cols = _angle.cols = nangle;
                # 计算邻域内每个点的 梯度角度
                cvCartToPolar(&matX, &matY, 0, &_angle, 1);

                float bestx = 0, besty = 0, descriptor_mod = 0;
                for (i = 0; i < 360; i += SURF_ORI_SEARCH_INC) // SURF_ORI_SEARCH_INC 为扇形区域扫描的步长
                {
                    float sumx = 0, sumy = 0, temp_mod;
                    for (j = 0; j < nangle; j++)
                    {
                        # d是 分析到的那个点与 现在主方向的偏度
                        int d = std::abs(cvRound(angle[j]) - i);
                        if (d < ORI_WIN / 2 || d > 360 - ORI_WIN / 2)
                        {
                            sumx += X[j];
                            sumy += Y[j];
                        }
                    }
                    temp_mod = sumx*sumx + sumy*sumy;
                    # descriptor_mod 是最大峰值
                    if (temp_mod > descriptor_mod)
                    {
                        descriptor_mod = temp_mod;
                        bestx = sumx;
                        besty = sumy;
                    }
                }
                descriptor_dir = fastAtan2(-besty, bestx);
            }
            kp.angle = descriptor_dir;
            if (!descriptors || !descriptors->data)
                continue;

            # 用特征点周围20*s为边长的邻域 计算特征描述子 
            int win_size = (int)((PATCH_SZ + 1)*s);
            CV_Assert(winbuf->cols >= win_size*win_size);
            Mat win(win_size, win_size, CV_8U, winbuf->data.ptr);

            if (!upright)
            {
                descriptor_dir *= (float)(CV_PI / 180); # 特征点的主方向 弧度值
                float sin_dir = -std::sin(descriptor_dir); # - sin dir
                float cos_dir = std::cos(descriptor_dir);

                float win_offset = -(float)(win_size - 1) / 2;
                float start_x = center.x + win_offset*cos_dir + win_offset*sin_dir;
                float start_y = center.y - win_offset*sin_dir + win_offset*cos_dir;
                uchar* WIN = win.data;

                int ncols1 = img->cols - 1, nrows1 = img->rows - 1;
                size_t imgstep = img->step;
                for (i = 0; i < win_size; i++, start_x += sin_dir, start_y += cos_dir)
                {
                    double pixel_x = start_x;
                    double pixel_y = start_y;
                    for (j = 0; j < win_size; j++, pixel_x += cos_dir, pixel_y -= sin_dir)
                    {
                        int ix = cvFloor(pixel_x), iy = cvFloor(pixel_y);
                        if ((unsigned)ix < (unsigned)ncols1 &&
                            (unsigned)iy < (unsigned)nrows1)
                        {
                            float a = (float)(pixel_x - ix), b = (float)(pixel_y - iy);
                            const uchar* imgptr = &img->at<uchar>(iy, ix);
                            WIN[i*win_size + j] = (uchar)
                                cvRound(imgptr[0] * (1.f - a)*(1.f - b) +
                                imgptr[1] * a*(1.f - b) +
                                imgptr[imgstep] * (1.f - a)*b +
                                imgptr[imgstep + 1] * a*b);
                        }
                        else
                        {
                            int x = std::min(std::max(cvRound(pixel_x), 0), ncols1);
                            int y = std::min(std::max(cvRound(pixel_y), 0), nrows1);
                            WIN[i*win_size + j] = img->at<uchar>(y, x);
                        }
                    }
                }
            }
            else
            {

                float win_offset = -(float)(win_size - 1) / 2;
                int start_x = cvRound(center.x + win_offset);
                int start_y = cvRound(center.y - win_offset);
                uchar* WIN = win.data;
                for (i = 0; i < win_size; i++, start_x++)
                {
                    int pixel_x = start_x;
                    int pixel_y = start_y;
                    for (j = 0; j < win_size; j++, pixel_y--)
                    {
                        int x = MAX(pixel_x, 0);
                        int y = MAX(pixel_y, 0);
                        x = MIN(x, img->cols - 1);
                        y = MIN(y, img->rows - 1);
                        WIN[i*win_size + j] = img->at<uchar>(y, x);
                    }
                }
            }

            resize(win, _patch, _patch.size(), 0, 0, INTER_AREA);

            for (i = 0; i < PATCH_SZ; i++)
            for (j = 0; j < PATCH_SZ; j++)
            {
                float dw = DW[i*PATCH_SZ + j]; # 高斯加权系数
                float vx = (PATCH[i][j + 1] - PATCH[i][j] + PATCH[i + 1][j + 1] - PATCH[i + 1][j])*dw;
                float vy = (PATCH[i + 1][j] - PATCH[i][j] + PATCH[i + 1][j + 1] - PATCH[i][j + 1])*dw;
                DX[i][j] = vx;
                DY[i][j] = vy;
            }

            // Construct the descriptor
            vec = descriptors->ptr<float>(k);
            for (kk = 0; kk < dsize; kk++)
                vec[kk] = 0;
            double square_mag = 0;
            if (extended)
            {
                # 128维描述子，考虑dx与dy的正负号
                for (i = 0; i < 4; i++)
                for (j = 0; j < 4; j++)
                {
                    # 每个方块内是一个5s * 5s的区域，每个方法由8个特征描述
                    for (int y = i * 5; y < i * 5 + 5; y++)
                    {
                        for (int x = j * 5; x < j * 5 + 5; x++)
                        {
                            float tx = DX[y][x], ty = DY[y][x];
                            if (ty >= 0)
                            {
                                vec[0] += tx;
                                vec[1] += (float)fabs(tx);
                            }
                            else {
                                vec[2] += tx;
                                vec[3] += (float)fabs(tx);
                            }
                            if (tx >= 0)
                            {
                                vec[4] += ty;
                                vec[5] += (float)fabs(ty);
                            }
                            else {
                                vec[6] += ty;
                                vec[7] += (float)fabs(ty);
                            }
                        }
                    }
                    for (kk = 0; kk < 8; kk++)
                        square_mag += vec[kk] * vec[kk];
                    vec += 8;
                }
            }
            else
            {
                # 64位描述子
                for (i = 0; i < 4; i++)
                for (j = 0; j < 4; j++)
                {
                    for (int y = i * 5; y < i * 5 + 5; y++)
                    {
                        for (int x = j * 5; x < j * 5 + 5; x++)
                        {
                            float tx = DX[y][x], ty = DY[y][x];
                            vec[0] += tx; vec[1] += ty;
                            vec[2] += (float)fabs(tx); vec[3] += (float)fabs(ty);
                        }
                    }
                    for (kk = 0; kk < 4; kk++)
                        square_mag += vec[kk] * vec[kk];
                    vec += 4;
                }
            }
            # 归一化 描述子 以满足 光照不变性
            vec = descriptors->ptr<float>(k);
            float scale = (float)(1. / (sqrt(square_mag) + DBL_EPSILON));
            for (kk = 0; kk < dsize; kk++)
                vec[kk] *= scale;
        }
    }
};