C语言实现LDPC码项目详解
1. 项目背景与需求分析
1.1 项目背景
在现代通信和数据存储系统中，纠错码技术被广泛应用于对传输或存储数据中的错误进行检测和校正。其中，LDPC（Low-Density Parity-Check，低密度奇偶校验）码是一种性能接近香农极限的前向纠错码，因其稀疏性和良好的译码性能而受到广泛关注。自从Gallager在20世纪60年代首次提出LDPC码以来，它们在数字通信、卫星通信、无线网络以及数据存储领域中都发挥了重要作用。
LDPC码的基本思想在于构造一个稀疏的奇偶校验矩阵（H矩阵），用以定义码字必须满足的奇偶校验关系。利用这种矩阵结构，可以构造出纠错能力很强的编码方案，同时译码时可以采用基于迭代算法（如置信传播算法、位翻转算法等）进行高效译码。
在实际工程中，LDPC码既可用作信道编码，也可用于存储系统的数据保护。其优点在于：
- 接近香农极限的性能：在噪声条件下能够以较低的信噪比实现可靠传输。
- 硬件实现简单：由于奇偶校验矩阵的稀疏性，使得编码和译码过程中的计算量大大降低，便于硬件实现。
- 灵活的参数设计：可以根据实际应用需求灵活设计码长、码率以及纠错能力。
本项目旨在使用C语言实现一个简单的LDPC码，包括编码和译码两个基本模块。为了便于说明，本文选择一个小尺寸的LDPC码实例，通过构造适当的奇偶校验矩阵和生成矩阵，完成对输入二进制消息的编码；同时，利用基于位翻转算法的迭代译码方法对接收到的码字进行纠错。
1.2 项目需求
本项目的主要需求如下：
-
LDPC码的构造
定义一个稀疏的奇偶校验矩阵H，要求H矩阵满足低密度性质，并尽可能方便构造对应的生成矩阵G。
为了简单起见，我们选择将H矩阵构造为标准型，即写成P∣I的形式，其中P为非奇异矩阵，I为单位矩阵。这样可以直接利用公式G = I | P^T构造出生成矩阵，从而完成编码过程。 -
编码模块
给定一个长度为k的二进制消息，利用生成矩阵G计算出对应的长度为n（n=k+r）的码字。编码过程仅需进行矩阵乘法和模2运算。
本示例中，我们选取n=6、k=3的LDPC码作为演示例子，即生成矩阵为3×6矩阵，编码时将消息（3位）与G相乘得到码字（6位）。 -
译码模块
对于LDPC码译码，常用的译码算法有置信传播算法和位翻转算法。由于置信传播算法较为复杂且涉及概率计算，而位翻转算法实现较为简单，适合教学示例，因此本项目选择基于位翻转算法的迭代译码方法。
译码模块的基本思想是：- 计算接收码字与奇偶校验矩阵H相乘得到综合症（syndrome）；
- 如果综合症全为0，则译码成功；
- 否则，计算每个位参与的奇偶校验错误数，选择错误数较多的比特进行翻转；
- 反复迭代直至综合症为零或达到预设的最大迭代次数。
-
错误处理与仿真测试
程序需要对内存分配、矩阵计算以及迭代过程中的异常情况进行检测，并给出详细的错误提示。主函数中应模拟发送端对消息进行编码，然后在信道中加入一定错误（例如翻转若干比特），最后调用译码模块进行纠错，验证LDPC码的纠错性能。 -
代码风格与注释
为便于初学者理解，本项目所有代码将写在同一文件中，并附有详细中文注释，解释每个函数的作用、输入输出参数及关键算法步骤。
通过上述需求，项目不仅可以帮助大家理解LDPC码的基本原理和实现方法，还能体会迭代译码算法中的误差检测与纠正机制，为更复杂的错误控制编码研究打下基础。
2. 设计思路与实现方案
2.1 LDPC码的参数与矩阵构造
为了使示例简单易懂，我们选取一个较小的LDPC码参数。令码长n=6，消息长度k=3，则冗余位数r=n-k=3。在构造标准型奇偶校验矩阵H时，我们要求其写成P∣I形式，其中P为3×3矩阵，I为3×3单位矩阵。例如，可以令
则奇偶校验矩阵H为
而生成矩阵G则为
2.2 译码算法选择
LDPC译码算法中，置信传播算法（Belief Propagation）是性能最优的一类算法，但实现较为复杂，涉及概率消息的更新与归一化。为了便于实现和教学，本项目采用位翻转（Bit-Flipping）算法。其基本步骤如下：
- 计算综合症：
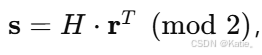，其中r为接收码字。 - 若综合症全为零，则译码成功。
- 否则，对每一位比特，统计其参与的奇偶校验方程中不满足条件的个数。
- 选择错误数超过某个阈值的比特进行翻转（从0变1或1变0）。
- 重复上述步骤直至综合症为零或达到最大迭代次数。
位翻转算法虽然简单，但对于小尺寸LDPC码可以实现良好效果，同时便于理解LDPC译码中的误差检测思想。
2.3 程序模块设计
本项目代码主要分为以下模块：
-
数据结构定义
利用二维数组定义奇偶校验矩阵H和生成矩阵G。此外，定义向量数据结构（使用数组）表示消息、码字和接收向量。 -
编码函数
实现函数encodeLDPC，接收输入消息向量，利用生成矩阵G计算码字。过程包括逐位相乘累加并模2运算。 -
综合症计算函数
实现函数sComputeSyndrome，利用奇偶校验矩阵H计算给定码字的综合症，用于译码判断。 -
译码函数
实现函数decodeLDPC，采用位翻转算法进行译码。函数输入为接收码字和最大迭代次数，输出译码后的码字及是否译码成功的标志。 -
辅助函数
包括打印向量、矩阵以及比特翻转操作的函数，便于调试和测试。 -
主函数
主函数中模拟一个完整的通信链路：- 随机生成一个消息，调用编码函数得到码字；
- 模拟信道传输时加入一定噪声（随机翻转若干比特）；
- 调用译码函数对接收到的码字进行纠错，并输出译码前后结果以及是否成功纠错。
2.4 错误处理与内存管理
由于C语言没有自动垃圾回收机制，本项目中所有动态分配的内存（如用于存储消息、码字等的数组）均需在不再使用时释放。此外，在矩阵运算和迭代译码过程中，应对边界条件和迭代次数进行判断，防止无限循环或数组越界。
2.5 代码风格与注释
所有代码将写在同一文件中，保证结构清晰。每个函数均附有详细中文注释，说明其输入、输出、功能以及关键实现步骤，方便初学者理解LDPC码的基本思想和实现方法。
3. 完整代码及详细注释
下面给出完整的C语言代码。代码中包含了LDPC编码与译码的所有核心操作，并附有详细中文注释，解释每个函数的作用和关键算法。请直接将以下代码复制到C文件中编译运行。
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <time.h>
// 定义LDPC码参数：码长 n = 6，消息长度 k = 3，冗余位 r = 3
#define N 6
#define K 3
#define R (N - K)
// 定义最大迭代次数，用于译码算法
#define MAX_ITER 20
// ---------------------------
// 矩阵定义：采用二维数组存储
// ---------------------------
// 生成矩阵 G = [I | P^T]，大小为 K x N，即 3 x 6
// 这里我们采用标准构造方法，其中 P 为 3x3矩阵
// 设 P = [ [1, 0, 1],
// [0, 1, 1],
// [1, 1, 0] ]
// 则 G = [ I_3 | P^T ] =
// [ 1 0 0 | 1 0 1 ]
// [ 0 1 0 | 0 1 1 ]
// [ 0 0 1 | 1 1 0 ]
int G[K][N] = {
{1, 0, 0, 1, 0, 1},
{0, 1, 0, 0, 1, 1},
{0, 0, 1, 1, 1, 0}
};
// 奇偶校验矩阵 H = [P | I], 大小为 R x N，即 3 x 6
// P 为 3x3矩阵，I 为 3x3单位矩阵
// 根据上面的P矩阵：
// H = [ [1, 0, 1, 1, 0, 0],
// [0, 1, 1, 0, 1, 0],
// [1, 1, 0, 0, 0, 1] ]
int H[R][N] = {
{1, 0, 1, 1, 0, 0},
{0, 1, 1, 0, 1, 0},
{1, 1, 0, 0, 0, 1}
};
// ---------------------------
// 辅助函数：打印向量、矩阵等
// ---------------------------
// 打印一个长度为 len 的二进制向量（数组）
void printVector(const char *label, const int vector[], int len) {
printf("%s: ", label);
for (int i = 0; i < len; i++) {
printf("%d ", vector[i]);
}
printf("\n");
}
// 打印一个矩阵，行数为 rows，列数为 cols
void printMatrix(const char *label, int matrix[][N], int rows, int cols) {
printf("%s:\n", label);
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
printf("%d ", matrix[i][j]);
}
printf("\n");
}
}
// ---------------------------
// 编码函数：LDPC编码
// ---------------------------
/*
* 函数名称: encodeLDPC
* 功能: 利用生成矩阵G对输入消息进行LDPC编码，得到码字
* 参数:
* message: 输入消息向量，长度为 K（二进制比特）
* codeword: 输出码字向量，长度为 N
* 返回值:
* 无，结果存储在 codeword 数组中
*
* 说明:
* 1. 编码过程为矩阵乘法：codeword = message * G (mod 2)
* 2. 逐位相乘并累加，最后对2取模
*/
void encodeLDPC(const int message[K], int codeword[N]) {
// 对码字每一位初始化为0
for (int j = 0; j < N; j++) {
codeword[j] = 0;
}
// 遍历生成矩阵G
for (int i = 0; i < K; i++) {
for (int j = 0; j < N; j++) {
codeword[j] = (codeword[j] + message[i] * G[i][j]) % 2;
}
}
}
// ---------------------------
// 译码函数：LDPC译码（基于位翻转算法）
// ---------------------------
/*
* 函数名称: computeSyndrome
* 功能: 计算综合症 s = H * r^T (mod 2)
* 参数:
* received: 输入的码字向量，长度为 N
* syndrome: 输出的综合症向量，长度为 R
* 返回值:
* 无，结果存储在 syndrome 数组中
*
* 说明:
* 1. 综合症用于检测码字是否满足所有奇偶校验约束
* 2. 若 syndrome 全为 0，则说明码字满足奇偶校验
*/
void computeSyndrome(const int received[N], int syndrome[R]) {
for (int i = 0; i < R; i++) {
syndrome[i] = 0;
for (int j = 0; j < N; j++) {
syndrome[i] = (syndrome[i] + H[i][j] * received[j]) % 2;
}
}
}
/*
* 函数名称: syndromeIsZero
* 功能: 判断综合症是否全为 0
* 参数:
* syndrome: 综合症向量，长度为 R
* 返回值:
* 1 表示综合症全为 0（译码成功），0 表示有错误
*/
int syndromeIsZero(const int syndrome[R]) {
for (int i = 0; i < R; i++) {
if (syndrome[i] != 0) {
return 0;
}
}
return 1;
}
/*
* 函数名称: decodeLDPC
* 功能: 对接收的码字进行LDPC译码（基于位翻转算法），试图纠正错误
* 参数:
* received: 输入的接收码字向量，长度为 N（可能含有错误）
* decoded: 输出的译码后码字向量，长度为 N
* max_iter: 最大迭代次数
* 返回值:
* 0 表示译码成功（综合症全为0），非0表示译码失败
*
* 说明:
* 1. 译码过程为迭代过程：计算综合症，若非0则判断每个位翻转后对综合症的改善
* 2. 采用简单位翻转策略：对每个位计算参与的奇偶校验约束不满足的个数，若超过一定阈值则翻转该比特
* 3. 本示例中采用较简单的策略，适用于小尺寸LDPC码，实际中可采用更复杂的置信传播算法
*/
int decodeLDPC(const int received[N], int decoded[N], int max_iter) {
// 将接收码字复制到译码数组中，作为初始猜测
memcpy(decoded, received, sizeof(int) * N);
int syndrome[R];
int iter = 0;
int error_corrected = 0;
while (iter < max_iter) {
computeSyndrome(decoded, syndrome);
if (syndromeIsZero(syndrome)) {
// 译码成功
return 0;
}
// 对每个位统计它参与的错误校验方程个数
int unsatisfiedCount[N] = {0};
// 遍历每个校验方程（行）
for (int i = 0; i < R; i++) {
// 如果第 i 个校验方程不满足（即 syndrome[i] == 1）
if (syndrome[i] == 1) {
// 遍历该行，统计每个比特参与错误校验的次数
for (int j = 0; j < N; j++) {
if (H[i][j] == 1) {
unsatisfiedCount[j]++;
}
}
}
}
// 找出参与错误校验次数最多的比特
int maxUnsat = 0;
int bitToFlip = -1;
for (int j = 0; j < N; j++) {
if (unsatisfiedCount[j] > maxUnsat) {
maxUnsat = unsatisfiedCount[j];
bitToFlip = j;
}
}
// 如果没有发现明显错误位，则退出
if (bitToFlip == -1 || maxUnsat == 0) {
break;
}
// 翻转该比特
decoded[bitToFlip] = (decoded[bitToFlip] == 0) ? 1 : 0;
error_corrected++;
iter++;
}
// 重新计算综合症，检查是否成功译码
computeSyndrome(decoded, syndrome);
if (syndromeIsZero(syndrome)) {
return 0;
} else {
return -1; // 译码失败
}
}
// ---------------------------
// 主函数：演示LDPC码的编码与译码
// ---------------------------
int main() {
// 设置随机数种子
srand((unsigned)time(NULL));
// 模拟发送端生成随机消息，长度为 K（3比特）
int message[K];
printf("生成随机消息:\n");
for (int i = 0; i < K; i++) {
message[i] = rand() % 2;
}
printVector("原始消息", message, K);
// 进行LDPC编码，生成码字（长度为 N = 6）
int codeword[N];
encodeLDPC(message, codeword);
printVector("编码得到的码字", codeword, N);
// 模拟信道传输，在码字中引入错误
// 例如随机翻转1个比特
int received[N];
memcpy(received, codeword, sizeof(int) * N);
int errorIndex = rand() % N;
received[errorIndex] = (received[errorIndex] == 0) ? 1 : 0;
printf("\n在传输过程中，第 %d 位发生错误！\n", errorIndex);
printVector("接收码字", received, N);
// 进行LDPC译码，尝试纠正错误
int decoded[N];
int ret = decodeLDPC(received, decoded, MAX_ITER);
if (ret == 0) {
printf("\n译码成功！\n");
} else {
printf("\n译码失败！\n");
}
printVector("译码后码字", decoded, N);
// 检验译码后码字是否正确（比较与原始码字是否一致）
int success = 1;
for (int i = 0; i < N; i++) {
if (decoded[i] != codeword[i]) {
success = 0;
break;
}
}
if (success) {
printf("译码结果正确，纠正了信道错误。\n");
} else {
printf("译码结果错误，未能完全纠正信道错误。\n");
}
return 0;
}
4. 代码解读
下面对代码中的主要部分进行详细解读，帮助大家深入理解整个实现过程及各个函数的作用。
4.1 数据结构与矩阵定义
-
参数定义
使用宏定义设置码长 (N=6) 与消息长度 (K=3) 以及最大迭代次数 (MAX_ITER=20)。这些参数决定了LDPC码的基本结构和译码过程中的迭代上限。 -
生成矩阵 G 与奇偶校验矩阵 H
通过标准形式构造LDPC码：- 生成矩阵G构造为 I | P^T；
- 奇偶校验矩阵H构造为 [P∣I]。
本示例中选取的P矩阵为
因此生成矩阵G和H如代码中所示。
4.2 编码函数 encodeLDPC
- 功能
将输入的消息向量与生成矩阵G进行矩阵乘法（模2运算），得到码字。 - 实现细节
对于每一列j，遍历所有消息位i进行累加，最后模2取余。注重对二维数组的下标处理和模运算。
4.3 综合症计算函数 computeSyndrome 与辅助函数
- computeSyndrome
利用奇偶校验矩阵H对输入码字计算综合症，检测是否满足所有奇偶校验约束。 - syndromeIsZero
判断综合症向量是否全为零，用于确定译码是否成功。
4.4 译码函数 decodeLDPC
- 算法思路
采用基于位翻转的简单译码算法：- 初始将接收码字作为译码初值。
- 计算综合症，如果全为0则译码成功。
- 否则，对于每个奇偶校验不满足的行，统计每个位在错误校验方程中出现的次数；
- 找出参与错误校验次数最多的比特并翻转；
- 迭代上述步骤，直至综合症全为零或迭代次数达到上限。
- 实现注意
由于本示例LDPC码尺寸较小，位翻转算法足够简单；对于实际系统中大尺寸LDPC码，通常需要更复杂的迭代译码算法（如置信传播算法）。
4.5 主函数 main
- 流程
- 生成随机消息并打印。
- 利用encodeLDPC编码生成码字。
- 模拟信道传输中随机翻转一个比特引入错误，并打印接收码字。
- 调用译码函数decodeLDPC进行纠错，并输出译码后的码字。
- 最后比较译码后码字与原始码字，验证译码是否成功纠正错误。
5. 项目总结与扩展思考
5.1 项目总结
本项目使用C语言实现了一个简单的LDPC码，包括编码和基于位翻转算法的译码模块。通过本项目，你可以了解到：
- LDPC码的构造与编码
利用标准型奇偶校验矩阵和生成矩阵，将消息编码为具有纠错能力的码字。 - 迭代译码思想
基于综合症的计算和位翻转策略，演示了如何利用LDPC码进行错误检测和纠正。 - 模块化编程
将编码、综合症计算、译码等功能模块化封装，便于调试和后续扩展。 - 仿真测试
通过模拟信道中引入错误并进行译码，验证了LDPC码在简单情形下的纠错性能，为后续更复杂系统的研究提供了实践基础。
5.2 扩展与改进
本项目作为LDPC码实现的入门案例，仍有许多扩展方向和改进空间，例如：
-
更高效的译码算法
本示例采用简单的位翻转算法，适用于小尺寸LDPC码。对于实际应用中常见的高码长LDPC码，建议实现置信传播（Belief Propagation）或最小和（Min-Sum）算法，以获得更好的译码性能。 -
动态参数配置
将LDPC码的参数（如码长、消息长度、最大迭代次数等）通过配置文件或命令行参数动态指定，提高程序的灵活性和适应性。 -
矩阵存储优化
由于LDPC码的奇偶校验矩阵H通常是稀疏矩阵，实际中可采用压缩稀疏矩阵（Compressed Sparse Row, CSR）等数据结构存储，从而节省内存和提高计算效率。 -
硬件加速
对于实时通信系统，译码算法的计算速度至关重要。可考虑利用SIMD指令或GPU加速技术对LDPC译码算法进行并行化，实现硬件加速。 -
仿真平台集成
将本项目作为模块集成到更大规模的通信仿真平台中，对不同信噪比下的纠错性能进行统计和分析，为实际系统设计提供理论依据。 -
扩展到非二进制LDPC码
虽然本示例实现的是二进制LDPC码，但LDPC码也可推广到更高阶域，支持更高维度的编码。研究和实现非二进制LDPC码也将是一项具有挑战性的工作。
5.3 项目反思
在本项目实现过程中，我们深刻体会到以下几点：
-
算法选择与实现平衡
尽管置信传播算法译码性能优异，但其实现复杂度较高。对于教学和小规模实验，采用位翻转算法既能帮助初学者理解LDPC译码基本原理，又能较快完成实现。 -
矩阵运算与模2运算的细节
编码和译码过程中的矩阵乘法和模2运算要求对数组下标和循环边界有严格控制，任何错误都可能导致译码失败或结果错误。 -
迭代终止条件设计
译码迭代算法中设置合适的最大迭代次数十分关键，过少可能导致未纠正完错误，过多则可能增加不必要的计算负担。需要根据具体应用进行权衡。 -
测试与仿真验证
通过对随机消息进行编码、加入噪声再译码，可以直观地验证LDPC码的纠错能力。未来还可设计更多测试用例，统计在不同错误率下的译码成功率，以全面评估系统性能。
5.4 实际应用场景
LDPC码在现代通信与数据存储系统中有广泛应用，主要包括：
-
无线通信与卫星通信
LDPC码因其接近香农极限的性能，被用于4G/5G、Wi-Fi以及卫星通信系统中，确保数据在噪声环境下高效传输。 -
数字电视与光纤通信
数字电视、光纤网络等高数据率传输系统中，LDPC码用于实现高效纠错，保证图像和视频质量。 -
数据存储系统
在硬盘、固态存储器及分布式存储系统中，LDPC码用于对数据进行冗余编码，防止因介质缺陷或读写错误而导致的数据丢失。 -
高速数据链路
在局域网和数据中心高速互联中，LDPC码帮助提高信道利用率和数据传输的鲁棒性。
6. 总结
本文详细介绍了如何使用C语言实现LDPC码，从项目背景、需求分析、设计思路、完整代码实现、代码详细解读到项目总结与扩展思考，层层解析了LDPC码的构造、编码和基于位翻转的译码方法。通过本项目，读者不仅能够掌握利用生成矩阵进行LDPC编码的基本方法，还能理解如何利用奇偶校验矩阵检测错误以及如何通过迭代译码进行错误纠正。
LDPC码在现代通信系统中具有极高的应用价值，其纠错性能和硬件实现优势使其成为众多标准的核心组成部分。虽然本项目示例规模较小，但所展示的编码与译码原理为更大规模LDPC码的研究与实现提供了基础。希望本篇博客能为你在通信原理、错误控制编码及算法实现等领域提供有益的指导，并激发你进一步探索更高效译码算法和硬件加速实现等前沿技术的兴趣。
在今后的工作中，你可以基于本项目扩展更复杂的LDPC译码算法（如置信传播算法）、支持稀疏矩阵存储和并行计算，并结合仿真平台对系统性能进行深入研究，从而不断提升分布式通信系统的鲁棒性和数据传输效率。
7. 参考资料
在本项目实现过程中，参考了以下资料和文献：
- Richardson, T. and Urbanke, R. "Modern Coding Theory", Cambridge University Press.
- MacKay, D.J.C. "Information Theory, Inference, and Learning Algorithms", Cambridge University Press.
- 论文 “Low-Density Parity-Check Codes” – Gallager, R.G.
- LDPC码在数字通信系统中的应用及译码算法相关文献。
- C语言矩阵运算与模2运算实现的相关教程与开源项目。
扫一扫
550
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
