LDPC编码学习

1 线性分组码

线性分组码是将信息序列划成固定长度的分组，包含监督位和信息位，并且两者呈线性关系。
eg：R=k/n的线性码（n,k）
将k bit的信息线性映射到n bit的码字

由于（n,k）的线性分组码C 是GF(2)上的所有 n 维向量组成的向量，空间的一个 k 维子空间，所以在 C 中一定可以找到 k 个相互线性独立的码字构成一组基向量，使得 C 中的每个码字都可以用这组基向量的线性组 合 来 表 示

                                        c=s·G

s：消息序列
c：编码后的码字
G：c的生成矩阵

与生成矩阵对应必定存在描述线性分组码的校验矩阵H

根据校验校验方程，可以判断某个码字是否为有效码字，因此C可以由校验矩阵唯一确定。

当得知校验矩阵以及待编码的信息位时，就可以通过校验方程组来反推出监
督位。因此对于给定的线性分组码只要找到校验矩阵或者生成矩阵就可以完成编
码操作。
线性分组码在译码时就是在所有的码字序列中寻找与接受序列最为接近的码
字作为译码结果。将在接收端接收的序列表示为r=c+e，e 为接收序列与发送的
码字序列的差，称为码字 c 的错误图样。将接收序列与校验矩阵相乘可以得到：

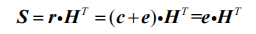
S :接收矢量的校正子，通过 S 和校验矩阵 H 可以反推出错误图样 e，在将
其与接收序列 r 相减，从而得出码字 c 完成译码

2 .校验矩阵的构成

随机构造发：Gallager构造发、旋转矩阵构造法，PEG构造法
结构构造发：由几何、代数、组合等方法构造，如准循环构造法

2.1 Gallager 构造法

构造（n,j,k）规则的的LDPC的校验矩阵的方法、

function GaH=GallagerH(CodeLength,dv,dc)
%%%
CodeLength=20;
dv=3;
dc=4