项目背景与概述
布莱克-斯科尔斯期权定价模型(Black-Scholes Option Pricing Model)是金融工程学中的一个重要理论,它提供了通过当前股票价格、执行价格、到期时间、无风险利率以及股票价格波动率来计算期权价格的方法。这个模型广泛应用于期权市场中,尤其是对于欧式期权的定价。
在本项目中,我们将用C++实现一个简化版的布莱克-斯科尔斯期权定价模型,包括计算欧式看涨期权和欧式看跌期权的理论价格。
相关概念
-
布莱克-斯科尔斯期权定价模型: 布莱克-斯科尔斯模型假设市场是完全的,且没有交易成本。它给出了期权的理论价格公式,尤其对于欧式期权,期权的价格是由以下因素决定的:
- 当前股票价格(S)
- 执行价格(K)
- 到期时间(T)
- 无风险利率(r)
- 股票价格的波动率(σ)
公式(欧式看涨期权):
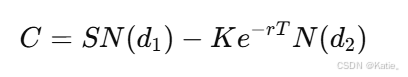
公式(欧式看跌期权):

其中:
-
欧式看涨期权(European Call Option): 欧式看涨期权是一种在期权到期时才能行使的期权。它允许购买者以执行价格(K)买入标的资产(通常是股票)。
-
欧式看跌期权(European Put Option): 欧式看跌期权是与看涨期权相对的,它允许购买者以执行价格(K)卖出标的资产。
-
标准正态分布(Standard Normal Distribution): 标准正态分布的累积分布函数 N(x) 用来计算标准正态分布的值,它是一个广泛应用于金融建模的函数。
项目实现思路
本项目的目标是使用C++实现布莱克-斯科尔斯期权定价模型,计算欧式看涨期权和欧式看跌期权的理论价格。主要步骤如下:
-
计算标准正态分布的累积分布函数(CDF): 由于C++标准库并不直接提供标准正态分布的CDF函数,我们需要自定义一个函数来计算它。
-
实现布莱克-斯科尔斯期权定价公式: 根据给定的参数(股票价格、执行价格、到期时间、无风险利率、波动率),实现布莱克-斯科尔斯模型的公式,分别计算看涨期权和看跌期权的价格。
-
输出计算结果: 在主函数中,根据用户输入的参数调用定价函数,计算并输出欧式期权的理论价格。
C++实现代码
#include <iostream>
#include <cmath>
#include <iomanip>
using namespace std;
// 标准正态分布的累积分布函数(CDF)
double norm_cdf(double x) {
return 0.5 * erfc(-x / sqrt(2)); // erfc是C++标准库提供的互补误差函数
}
// 布莱克-斯科尔斯期权定价函数
double blackScholesCall(double S, double K, double T, double r, double sigma) {
// 计算d1和d2
double d1 = (log(S / K) + (r + 0.5 * sigma * sigma) * T) / (sigma * sqrt(T));
double d2 = d1 - sigma * sqrt(T);
// 计算看涨期权的价格
return S * norm_cdf(d1) - K * exp(-r * T) * norm_cdf(d2);
}
double blackScholesPut(double S, double K, double T, double r, double sigma) {
// 计算d1和d2
double d1 = (log(S / K) + (r + 0.5 * sigma * sigma) * T) / (sigma * sqrt(T));
double d2 = d1 - sigma * sqrt(T);
// 计算看跌期权的价格
return K * exp(-r * T) * norm_cdf(-d2) - S * norm_cdf(-d1);
}
int main() {
// 输入参数
double S, K, T, r, sigma;
cout << "Enter the current stock price (S): ";
cin >> S;
cout << "Enter the strike price (K): ";
cin >> K;
cout << "Enter the time to maturity (T in years): ";
cin >> T;
cout << "Enter the risk-free interest rate (r in decimals): ";
cin >> r;
cout << "Enter the volatility (sigma in decimals): ";
cin >> sigma;
// 计算欧式看涨期权和看跌期权的价格
double call_price = blackScholesCall(S, K, T, r, sigma);
double put_price = blackScholesPut(S, K, T, r, sigma);
// 输出结果
cout << fixed << setprecision(2);
cout << "European Call Option Price: " << call_price << endl;
cout << "European Put Option Price: " << put_price << endl;
return 0;
}
代码解读
-
norm_cdf函数: 由于C++标准库没有直接提供标准正态分布的累积分布函数,我们使用erfc(互补误差函数)来计算标准正态分布的CDF。互补误差函数与标准正态分布的CDF有直接关系。 -
blackScholesCall和blackScholesPut函数:- 这两个函数实现了布莱克-斯科尔斯公式,分别计算欧式看涨期权和看跌期权的理论价格。
- 函数内首先计算出d_1和d_2,然后根据公式计算期权价格。

-
main函数:- 在主函数中,用户输入股票价格、执行价格、到期时间、无风险利率和波动率等参数。
- 然后分别调用
blackScholesCall和blackScholesPut函数,计算并输出期权的价格。
项目总结
本项目实现了一个简化版的布莱克-斯科尔斯期权定价模型,用C++计算欧式看涨期权和看跌期权的理论价格。通过输入期权相关的参数,程序能够输出相应的期权价格。该模型是现代金融工程学中最重要的定价模型之一,广泛应用于期权市场。
未来扩展
-
计算美国期权:布莱克-斯科尔斯模型主要用于欧式期权,而美国期权可以在到期前任何时间行使,因此计算方法更为复杂。可以考虑实现类似的定价模型,如二叉树模型(Binomial Tree)或蒙特卡罗模拟。
-
考虑股息影响:可以扩展模型,考虑股票支付股息的情况,从而调整定价公式。
-
优化计算性能:对于大规模的期权定价需求,可以通过并行计算优化性能,尤其是对于蒙特卡罗模拟等复杂算法。
通过这些扩展,我们能够更加准确地模拟实际市场中的期权定价问题。


























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








