《算法导论》15.2 矩阵链乘法(含有C++代码)

一、问题背景

给定一个n个矩阵的序列(矩阵链)<A1，A2,…，An>，我们希望计算它们的乘积A1A2…An(15.5)
为了计算表达式(15.5)，我们可以先用括号明确计算次序，然后利用标准的矩阵相乘算法进行计算。
我们称有如下性质的矩阵乘积链为完全括号化的( fully parenthesized):它是单一矩阵， 或者是两个完全括号化的矩阵乘积链的积，且已外加括号。例如，如果矩阵链为(A1，A2, A3，A4>，则共有5种完全括号化的矩阵乘积链:


假设三个矩阵的规模分别为10X100、100X5 和5X50。如果按((A1A2)A3)的顺序计算，为计算
A1A2(规模10X5)，需要做10100 5=5000次标量乘法，再与A3相乘又需要做10550=2500次标量乘法，共需7500次标量乘法。如果按(A1 （A2A3))的顺序，计算A2A3(规模100X50)，需100550= 25000次标量乘法，A再与之相乘又需1010050= 50000次标量乘法，共需75 000次标量乘法。因此，按第一种顺序计算矩阵链乘积要比第二种顺序快10倍。

正题

矩阵链乘法问题(matrix chain multiplication problem)可描述如下:给定n个矩阵的链<A1，A2… An)，矩阵A的规模为p_i-1*p_i(1≤i≤n),求完全括号化方案，使得计算乘积A1…An所需标量乘法次数最少。
注意，求解矩阵链乘法问题并不是要真正进行矩阵相乘运算，我们的目标只是确定代价最低的计算顺序。确定最优计算顺序所花费的时间通常要比随后真正进行矩阵相乘所节省的时间(例如仅进行7500次标量乘法而不是75000次)要少。

利用动态规划方法

（1）最优括号化的结构特征

看到，一个非平凡的矩阵链乘法问题实例的任何解都需要划分链，而任何最优解都是由子问题
实例的最优解构成的。因此，为了构造一个矩阵链乘法问题实例的最优解，我们可以将问题划分为两个子问题(A_iA_i+1+…A_k和A_k+1+A_k+2…A_j;的最优括号化问题)，求出子问题实例的最优解，将子问题的最优解组合起来。我们必须保证在确定分割点时，已经考察了所有可能的划分点，这样就可以保证不会遗漏最优解。

（2）一个递归求解方案

用m[i…j]表示计算矩阵A_i…j所需标量乘法的最小值，那么原问题最优解就是m[1…n]。
递归定义m[i…j]如下，对于i=j时的平凡问题，矩阵链只包含唯一的矩阵A_i…i=A，因此不需要做任何标量乘法运算。所以，对所有i=1, 2, … n, m[i, i]=0。 若i < j,我们利用步骤1中得到的最优子结构来计算m[i,j]。我们假设A_iA_i+1A_j,的最优括号化方案的分割点在矩阵A_k和A_k+1之间，其中i≤k<j。那么，m[i, j]就等于计算A_i…k和A_k+1…j的代价加上两者相乘的代价的最小值。由于矩阵A_i的大小为p_i-1*p_i，易知A_i…k与A_k+1…j相乘的代价为p_i-1p_kp_j次运算。因此，我们得到
由于k的不确定性，我们得到以下递归求解公式：

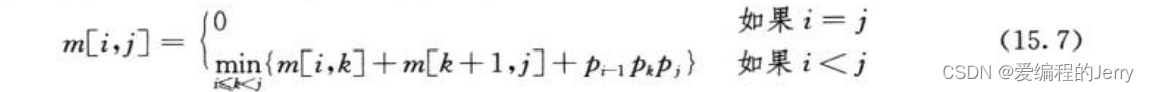
m[i,j]的值给出了子问题最优解的代价，但它并未提供足够的信息来构造最优解。为此，我们用s[i, j]保存A_i…A_j最优括号化方案的分割点位置k，即使得m[i, j]=m[i, k]+m[k+1, j]+p_i-1p_kp_j，成立的k值。

（3）计算最优代价

我们采用一种自底而上的方法：

MATRIX-CHAIN-ORDER(p)
n = p.length-1
let m[1...n,1..n] and s[1...n-1,2....n] be new tables
for i = 1 to n	//长度为1的链的最小代价
	m[i,i] = 0
//第一个循环步：利用递归公式对所有i = 1...n-1计算m[i...i+1]（长度为2的链最小代价）
for l = 2 to n	
	for(i = 1 to n - l + 1)
		j = i + l - 1
		m[i,j] = ∞
		for k = i to j-1
			q = m[i...k] + m[k+1,j] + pi-1 pk pj
			if q < m[i...j]
				m[i...j] = q	//保存代价
				s[i...j] = k	//保存分割点
return m and s

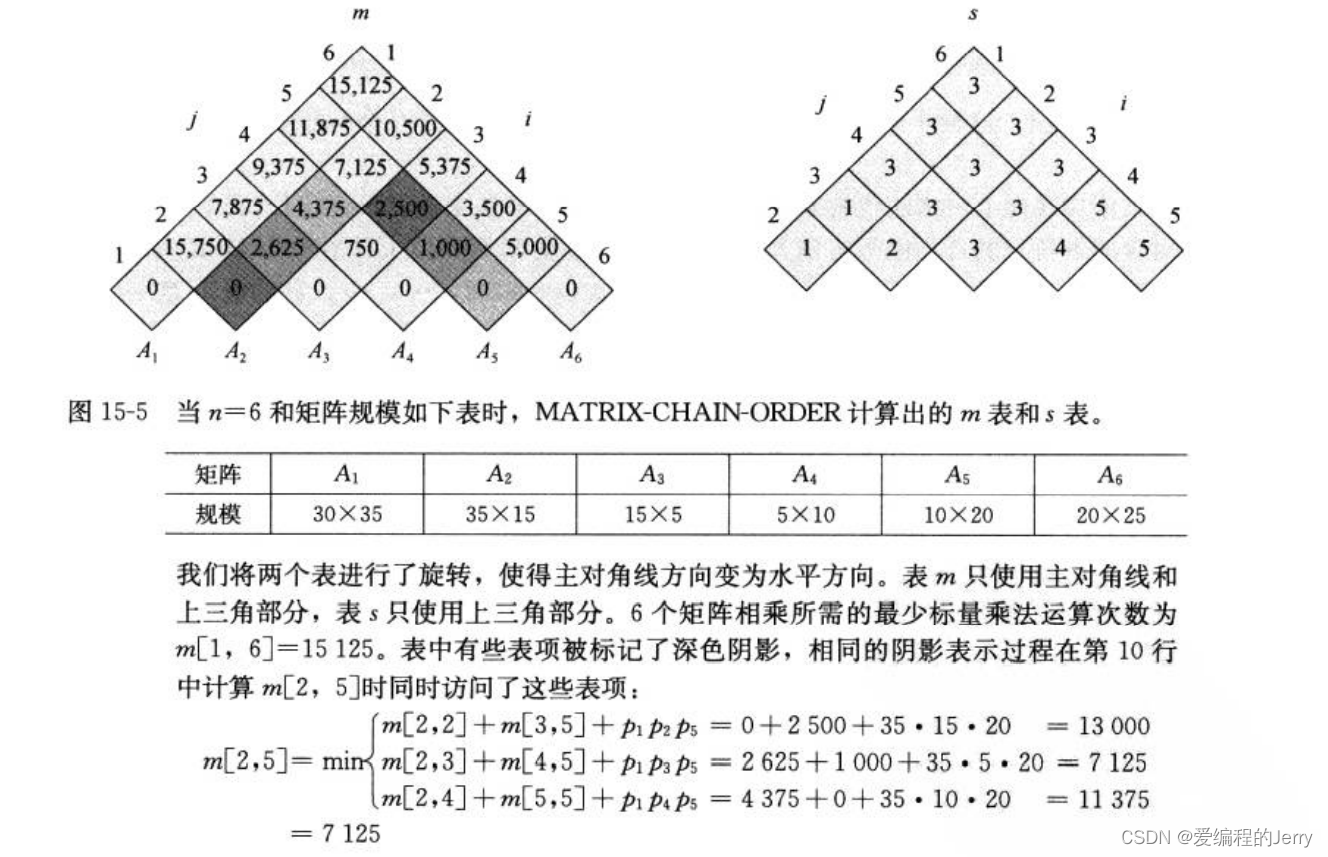
（4）构造最优解(没什么话可以忽略的)

PRINT-OPTIMAL-PARENS(s,j,i)
if i==j
	print("A"i)
else print "("
	PRINT-OPTIMAL-PARENS(s, i, s[i,j])
	PRINT-OPTIMAL-PARENS(s, s[i,j]+1, j)
	print ")"

C++代码

#include <iostream>
#include <vector>
using namespace std;
void MatrixChainOrder(vector<int>& v, int(*m)[10], int(*s)[10])
{
	int n = v.size() -1;
	int  q,num,j = 0;
	for (int i = 1; i < n; i++) {
		m[i][i] = 0;
	}
	for (int l = 2; l <= n; l++) {
		for (int i = 1; i <= n - l + 1;i++) {
			j = i + l - 1;
			m[i][j] = INT_MAX;
			for (int k = i; k <= j - 1; k++) {
				q = m[i][k]+m[k+1][j]+v[i-1]*v[k]*v[j];
				if (q < m[i][j]) {
					m[i][j] = q;
					s[i][j] = k;
				}
			}
		}
	}
}
void PrintOptimalParens(int(*s)[10], int i, int j)
{
	if (i == j)
	{
		cout << 'A'<<i;
	}
	else {
		cout << "(";
		PrintOptimalParens(s, i, s[i][j]);
		PrintOptimalParens(s, s[i][j] + 1, j);
		cout << ")";
	}
}
int main()
{
	vector<int>v1;
	int n;
	cout << "Please enter the number you want!" << endl;
	cin >> n;
	cout << "Please enter the numbers!" << endl;
	int number;
	for (int i = 0; i < n; i++) {
		cin >> number;
		v1.push_back(number);
	}
	int m[10][10], s[10][10];
	MatrixChainOrder(v1, m,s);
	cout << "result:" << endl;
	PrintOptimalParens(s, 1, 6);
	cout << endl;
	return 0;
}