NTC和温度的关系

梁善被人欺

已于 2025-03-20 09:40:27 修改

阅读量1k

点赞数 10

分类专栏： BMS 文章标签：网络单片机嵌入式硬件服务器数据结构

于 2023-12-18 17:30:27 首次发布

本文链接：https://blog.csdn.net/m0_61973119/article/details/135064134

版权

BMS 专栏收录该内容

27 篇文章

订阅专栏

一、NTC介绍

NTC（nagative temperature coefficient）负温度系数的热敏电阻。随着温度的升高，电阻越来越小

二、NTC和温度的关系

生产NTC的厂家会提供一个RT表格，里面记录了温度和电阻的关系，他们的关系是一一对应的，生成的曲线是非线性的

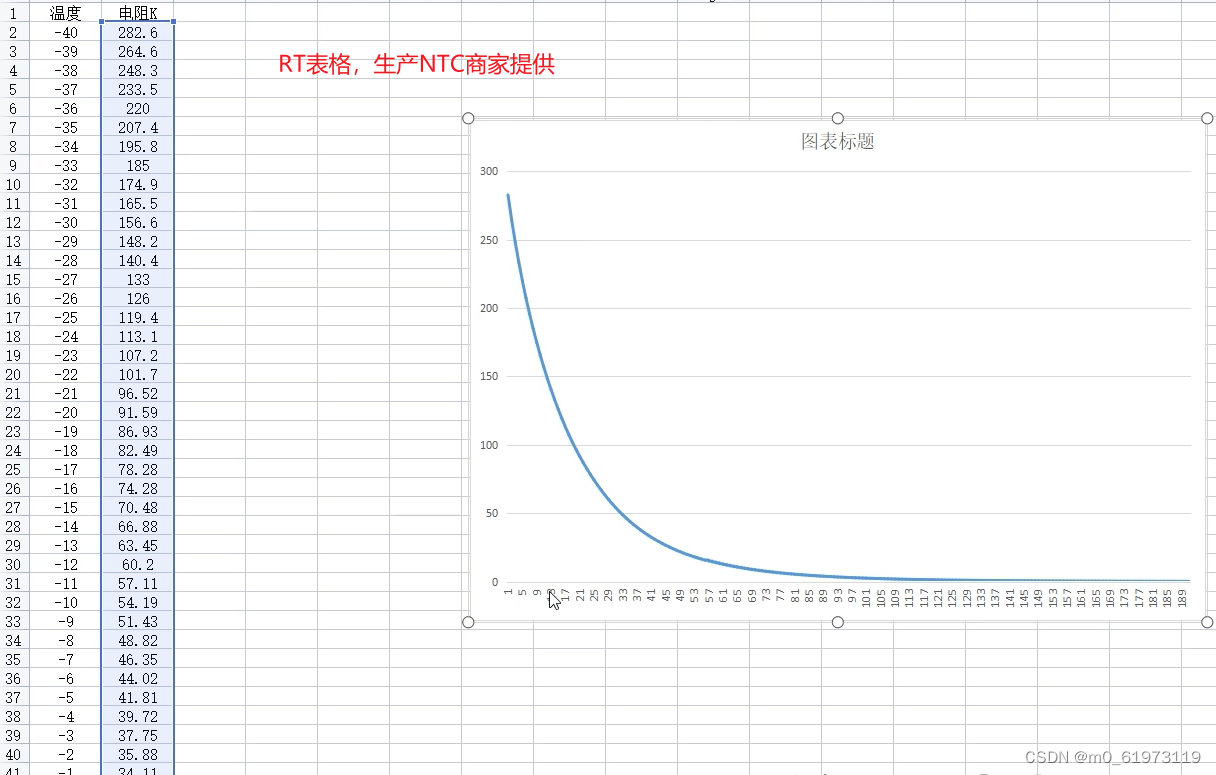
NTC测量温度的原理，看下图表格，左边电路图可以简化成右边的电路图，我们已知了R1，VIN(VREF）和Vout的的值（Vout的值可以测出来），然后在参考RT表格，我们就可以明确的知道此时的温度是多少。

三、代码编写（查表法）

针对温度需要显示到小数点后1位，如果只需要显示到整数，那么将二分查找函数返回条件修改会返回如果找不到固定值，则返回最接近目标值的下标

#include <stdio.h>

int arr[201] = {
    3003200, 2818890, 2646990, 2486590, 2336860, 2197030, 2066390, 1944290, 1830130, 1723340, // -40℃~-31℃
    1623400, 1529830, 1442200, 1360100, 1283160, 1211020, 1143350, 1079860, 1020270, 964310,  // -30℃~-21℃
    911740, 862410, 816020, 772390, 731320, 692670, 656270, 621990, 589680, 559230,           // -20℃~-11℃
    530520, 503380, 477770, 453600, 430790, 409240, 388890, 369660, 351480, 334300,           // -10℃~-1℃
    326560, 310414, 295155, 280730, 267087, 254182, 241970, 230410, 219466, 209100, 198920,   // 0℃~10℃
    187490, 178990, 170920, 163260, 155980, 149050, 142460, 136190, 130220, 124550,           // 11℃~20℃
    119140, 114000, 109110, 104440, 100000, 95745, 91693, 87832, 84154, 80648,                // 21℃~30℃
    77305, 74118, 71078, 68177, 65410, 62768, 60247, 57838, 55538, 53341,                     // 31℃~40℃
    51242, 49235, 47317, 45483, 43728, 42051, 40445, 38909, 37438, 36030,                     // 41℃~50℃
    34701, 33427, 32204, 31032, 29907, 28827, 27791, 26797, 25842, 24925,                     // 51℃~60℃
    24044, 23199, 22386, 21605, 20855, 20134, 19441, 18774, 18133, 17517,                     // 61℃~70℃
    16914, 16334, 15777, 15241, 14725, 14230, 13753, 13294, 12852, 12427,                     // 71℃~80℃
    12018, 11624, 11244, 10879, 10527, 10191, 9867, 9555, 9255, 8965,                         // 81℃~90℃
    8686, 8418, 8159, 7909, 7668, 7436, 7211, 6995, 6787, 6585,                               // 91℃~100℃
    6392, 6205, 6025, 5850, 5682, 5519, 5361, 5209, 5061, 4919,                               // 101℃~110℃
    4781, 4647, 4518, 4393, 4272, 4155, 4042, 3932, 3826, 3723,                               // 111℃~120℃
    3623, 3526, 3432, 3342, 3254, 3168, 3084, 3003, 2925, 2849,                               // 121℃~130℃
    2775, 2704, 2634, 2567, 2502, 2438, 2377, 2317, 2259, 2202,                               // 131℃~140℃
    2147, 2094, 2043, 1992, 1944, 1896, 1850, 1805, 1762, 1719,                               // 141℃~150℃
    1678, 1638, 1599, 1561, 1524, 1488, 1453, 1419, 1386, 1354                                // 151℃~160℃
};

// 数组从大到小排列，二分查找找不到对应值，返回偏大值的下标
int search(int arr[], int size, int target)
{
    int left = 0;
    int right = size - 1;
    int middle = 0;

    if (size <= 0) {
        return -1;
    }
    if (arr[right] >= target) {
        return right;
    }
    if (arr[left] < target) {
        return -1;
    }

    while (right >= left)
    {
        middle = (left + right) >> 1;
        if (target < arr[middle])
        {
            left = middle;
        }
        else if (target > arr[middle])
        {
            right = middle;
        }
        else
        {
            return middle;
        }
        if (right - left == 1) // 找不到目标值且即将返回-1
        {
            return left;
        }
    }
    return -1;
}


int main() {
    int indexDot=0,temp=0;//temp单位 0.1摄氏度
    int index = search(arr,sizeof(arr)/sizeof(arr[0]), 100000);
    if(index != -1)
    {
        indexDot = (arr[index] - 100000) * 10 / (arr[index] - arr[index + 1]);
        temp = (index - 40) * 10 + indexDot;
        printf("index = %d indexDot = %d temp = %d\r\n", index, indexDot, temp);
    }
    else
    {
        temp = 2000;//非法值
    }
    
}