区间DP入门笔记（3）猴子派对/石头组合 HDU-3506

问题 - 3506 (hdu.edu.cn)

 题意：n个猴子坐一圈，每次只能让相邻 两个/两队 进行组合，组合时要将 两个/两队 的权值加和并计入总和中，最后求总和的最小值。

思路：此题可以用区间DP求解，难点在于如何将其变为环的情况，因此介于操作的难易程度，采用开 2n 大小的数组以保证数组的头和尾可以进行运算。

DP状态转移方程：dp[i][j] = min(dp[i][j], dp[i][k] + dp[k + 1][j] + sum[j] - sum[i - 1]);

#include<iostream>
#define maxsize 1005
#define min(i,j) i<j?i:j

using namespace std;

int a[maxsize * 2] = { 0 };
int dp[maxsize * 2][maxsize * 2];
int sum[maxsize * 2];

int main() {
	int n;
	while (~scanf_s("%d", &n)) {
		memset(sum, 0, sizeof(int) * maxsize * 2);
		a[0] = 0;
		for (int i = 1; i <= n; i++) {
			scanf_s("%d", &a[i]);
			a[i + n] = a[i];
			memset(dp[i], 0x3f3f3f3f, sizeof(int) * maxsize * 2);
		}
		for (int i = 1; i <= 2 * n; i++) {
			dp[i][i] = 0;
			sum[i] = sum[i - 1] + a[i];
		}
		for (int d = 2; d <= n; d++) {
			for (int i = 1; i <= 2 * n - d + 1; i++) {
				int j = i + d - 1;
				for (int k = i; k < j; k++) {
					dp[i][j] = min(dp[i][j], dp[i][k] + dp[k + 1][j] + sum[j] - sum[i - 1]);
				}
			}
		}
		int ans = 0x3f3f3f3f;
		for (int i = 1; i <= n; i++) {
			ans = min(ans, dp[i][i + n - 1]);
		}
		printf("%d\n", ans);
	}
	return 0;
}

但是此代码过oj系统时会显示超时，因此这种做法显然需要进行一定的时间上的优化。此时时间复杂度为O()。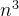

因此我们使用到了四边形优化，其大致原理为 a[ i`][ j ] + a[ i ][ j`] <= a[ i ][ j ] + a[ i`][ j` ].

其中 i`<= i <= j <= j`。

详细解释：

文章：(1条消息) 四边形不等式优化讲解（详解）_NOIAu的博客-CSDN博客_四边形不等式

视频：区间动态规划的四边形不等式优化_哔哩哔哩_bilibili

因此我们需要引入一个s[ i ][ j ]数组，来代表 i 和 j 区间内的最佳分割点，即当k=s[ i ][ j ]时 dp[i][k] + dp[k + 1][j] + sum[j] - sum[i - 1]为最优解。

#include<iostream>
#define maxsize 2100
#define min(i,j) (i<j)?i:j

using namespace std;

int a[maxsize];
int dp[maxsize][maxsize];
int sum[maxsize];
int s[maxsize][maxsize];

int main() {
	int n;
	while (~scanf_s("%d", &n)) {
		memset(dp, 0x3f3f3f3f, sizeof(dp));
		for (int i = 1; i <= n; i++) {
			scanf_s("%d", &a[i]);
			a[i + n] = a[i];
		}
		sum[0] = 0;
		for (int i = 1; i <= 2 * n; i++) {
			sum[i] = sum[i - 1] + a[i];
			dp[i][i] = 0;
			s[i][i] = i;
		}
		for (int d = 2; d <= n; d++) {
			for (int i = 1; i <= 2 * n - d + 1; i++) {
				int j = i + d - 1;
				for (int k = s[i][j - 1]; k <= s[i + 1][j]; k++) {
					if (dp[i][j] > dp[i][k] + dp[k + 1][j] + sum[j] - sum[i - 1]) {
						dp[i][j] = dp[i][k] + dp[k + 1][j] + sum[j] - sum[i - 1];
						s[i][j] = k;
					}
				}
			}
		}
		int ans = 0x3f3f3f3f;
		for (int i = 1; i <= n; i++) {
			ans = min(ans, dp[i][i + n - 1]);
		}
		printf("%d\n", ans);
	}
	return 0;
}

注意：

1.此题输出结果要求对多个输入样例都有运算，因此需要在输入n的时候加上while循环，即为：while (~scanf_s("%d", &n)){}

2.普通区间DP超时，需要时间上的优化。