WHU数据结构 | 排序

排序：整理表中的元素，使之按关键字递增或递减有序排列。
          本章仅讨论递增排序的情况，在默认情况下均指递增排序。

排序的稳定性：当待排序元素的关键字均不相同时，排序的结果是唯一的，否则排序的结果不一定唯一。
如果待排序的表中，存在有多个关键字相同的元素，经过排序后这些具有相同关键字的元素之间的相对次序保持不变，则称这种排序方法是稳定的。
反之，若具有相同关键字的元素之间的相对次序发生变化，则称这种排序方法是不稳定的。

---

---

排序数据的组织：以顺序表作为排序表的存储结构（除基数排序采用单链表外）。假设关键字为int类型，待排序的顺序表直接采用vector<int>向量R表示。

---

内排序：在排序过程中，若整个表都是放在内存中处理，排序时不涉及数据的内、外存交换。
外排序：在排序过程中要进行数据的内、外存交换。

---

内排序的分类：

基于比较的排序：1.比较 2.移动

排序算法的性能由算法的时间和空间确定的，而时间又是由比较和移动的次数确定的。

表中元素为正序：待排序元素的关键字顺序正好和排序顺序相同。
表中元素为反序：待排序元素的关键字顺序正好和排序顺序相反。

 

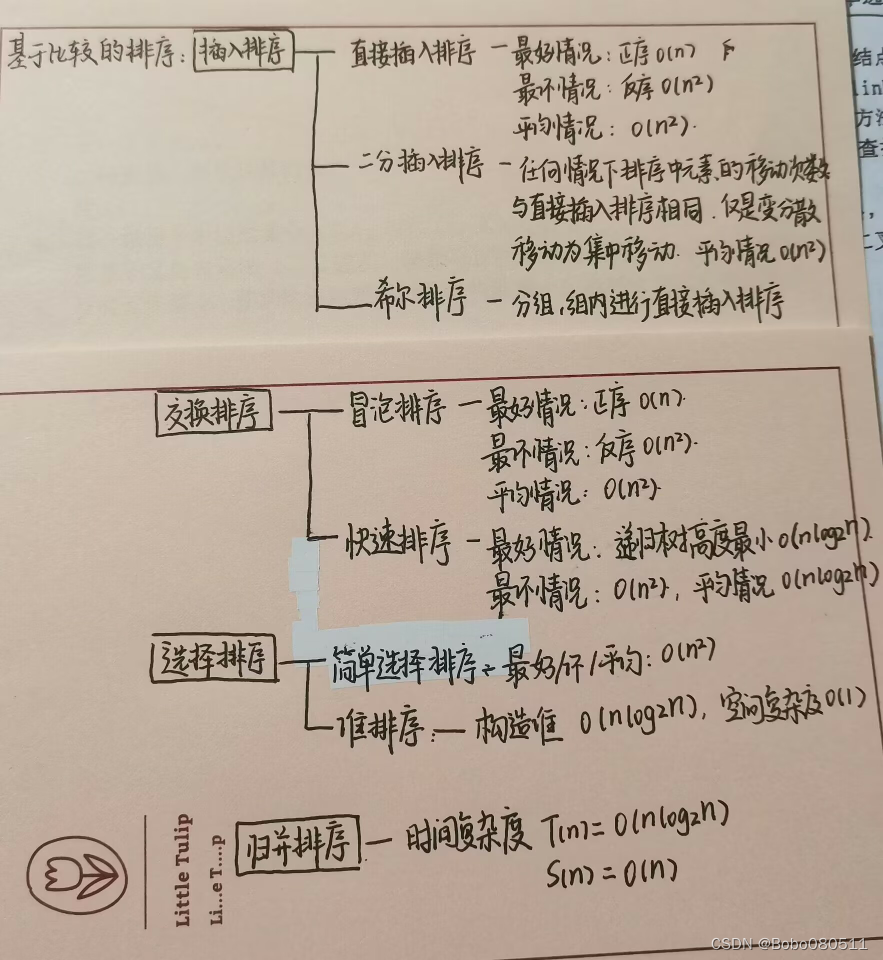
插入排序：

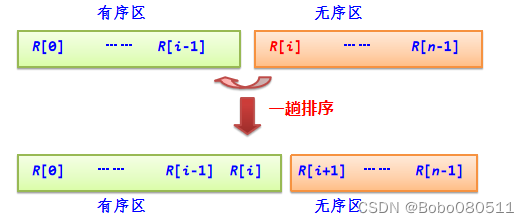
直接插入排序：共n个元素。初始时，有序区只有一个元素R[0]，共经过n-1趟排序。

在有序区中找到第一个小于R[i]的元素，在其后插入R[i]的值

//直接插入排序
void InsertSort(vector<int>& R,int n) 	
{  
 for (int i=1;i<n;i++)			//从R[1]开始
   {  
     if (R[i]<R[i-1])			//反序时
       { int tmp=R[i];			//取出无序区的第一个元素
         int j=i-1;		//有序区R[0..i-1]中向前找R[i]的插入位置

         do
         {  R[j+1]=R[j];			//将大于tmp的元素后移
            j--;				//继续向前比较
         } while (j>=0 && R[j]>tmp);

         R[j+1]=tmp;				//在j+1处插入R[i]
      }
   }
}

 算法扩展：

排序中通常利用“<”比较实现递增排序，可以自定义比较函数cmp(x,y)，

如x<y时，该函数返回true，否则返回false，这样将上述算法中R[j]<=tmp转换为!tmp<R[j]即!cmp(tmp，R[j])，

void InsertSort(vector<int>& R,int n) 	//直接插入排序（递增）
{  for (int i=1;i<n;i++)			//从R[1]开始
   {  if (cmp(R[i],R[i-1]))			//反序时
      {  int tmp=R[i];			//取出无序区的第一个元素
         int j=i-1;		//有序区R[0..i-1]中向前找插入位置

         do
         {  R[j+1]=R[j];			//将大于tmp的元素后移
            j--;				//继续向前比较
         } while (j>=0 && !cmp(R[j],tmp));

         R[j+1]=tmp;				//在j+1处插入R[i]
      }
   }
}

bool cmp(int x,int y)	  //实现递增排序的自定义比较函数
{  if (x<y) return true;
   else return false;
}

bool cmp(int x,int y)	  //实现递减排序的自定义比较函数
{  if (x>y) return true;
   else return false;
}

InsertSort算法不变即可递减排序R
后面讨论的各种排序算法都可以这样转换为递减排序或者按定制的方式排序

算法分析：

1.最好情况分析：

初始数据序列正序：时间复杂度为O(n)

2.最坏情况分析：

初始数据序列反序：时间复杂度为O(n^2)

3.平均情况分析：

将R[i]插入到R[0..i-1]（含i个元素）的中间位置：时间复杂度为O(n^2)

---

二分/折半插入排序：查找采用折半查找方法

void BinInsertSort(vector<int>& R,int n) 	//折半插入排序
{  for (int i=1;i<n;i++)			//从R[1]开始
   {  if (R[i]<R[i-1])			//反序时
      {  int tmp=R[i];			//将R[i]保存到tmp中


         int low=0,high=i-1;
         while (low<=high)		   //折半查找tmp的插入点high+1
         {  int mid=(low+high)/2;		//取中间位置
            if (tmp<R[mid])
               high=mid-1;			//插入点在左半区
            else
               low=mid+1;			//插入点在右半区
         }

         for (int j=i-1;j>=high+1;j--)	//元素后移
            R[j+1]=R[j];

         R[high+1]=tmp;			//原R[i]插入到R[high+1]中 
      }	
   }
}

算法分析：

在任何情况下排序中元素移动的次数与直接插入排序的相同，不同的仅是变分散移动为集中移动。平均情况的时间复杂度为O(n2)。

---

希尔排序：将n个元素分成d个组

d=n/2；将排序序列分为d个组，在各组内进行直接插入排序；递减d=d/2，重复，直到d=0为止

void ShellSort(vector<int>& R,int n) 	//希尔排序
{  int d=n/2;				//增量置初值

   while (d>0)
   { 
     for (int i=d;i<n;i++)		//相隔d位置的元素组直接插入排序
      {  if (R[i]<R[i-d])		//反序时
         {  int tmp=R[i];
            int j=i-d;
            do
            {  R[j+d]=R[j];		//将大于tmp的元素同组中后移
               j=j-d;			//继续向前比较
            } while (j>=0 && R[j]>tmp);
            R[j+d]=tmp;		//在j+d处插入R[i]
         }
      }

      d=d/2;				//减小增量
   }
}

算法分析：

1.希尔算法的时间复杂度难以分析，一般认为其平均时间复杂度为O(n^1.58)。

希尔排序的速度通常要比直接插入排序快。

2.希尔排序是一种不稳定的排序算法

一般地，相距位置较大的两个元素发生交换 →不稳定！

---

交换排序：两个元素反序时进行交换

冒泡排序：

初始有序区为空。i＝0~（n-2），共n-1趟使整个数据有序。→有序区总是全局有序的

 在冒泡排序算法中，若某一趟没有出现任何元素交换，说明所有元素已排好序了，就可以结束本算法。

void BubbleSort(vector<int>& R,int n) 	//冒泡排序
{  for (int i=0;i<n-1;i++) 
   {  
      bool exchange=false;		//本趟前将exchange置为false

      for (int j=n-1;j>i;j--)		//在无序区找出最小元素
          if (R[j]<R[j-1])		//反序时交换
          {  swap(R[j],R[j-1]);
             exchange=true;		//本趟发生交换置exchange为true
          }

      if (!exchange)			//本趟没有发生交换，中途结束算法
         return;
   }
}

算法分析：

1.最好情况分析：

初始数据序列正序：时间复杂度为O(n)。

2.最坏情况分析：

初始数据序列反序：时间复杂度为O(n^2)

3.平均情况分析：

算法可能在中间的某一趟排序完成后就结束，但平均的排序趟数仍是O(n)。
每一趟的关键字比较次数和元素移动次数为O(n)，所以平均时间复杂度为O(n^2)。

---

快速排序:

每趟使表的第1个元素放入适当位置（归位），将表一分为二，对子表按递归方式继续这种划分，直至划分的子表长为0或1（递归出口）。

 划分算法设计：

      n个元素共比较n-1次

排序算法设计：

void _QuickSort(vector<int>& R,int s,int t)  //对R[s..t]快速排序
{  
  if (s<t)				//表中至少存在两个元素的情况
   {  int i=Partition3(R,s,t);	//可用3种划分算法任意一种
      _QuickSort(R,s,i-1);		//对左子表递归排序
      _QuickSort(R,i+1,t);		//对右子表递归排序
   }
}
 
void QuickSort(vector<int>& R,int n)	 //快速排序
{
   _QuickSort(R,0,n-1);
}

快速排序过程 → 递归树

 

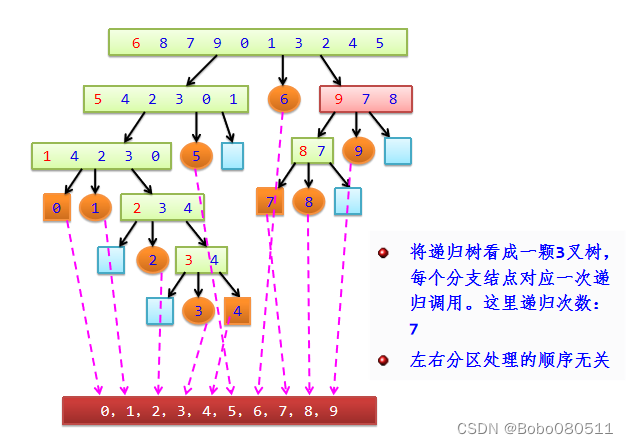
 算法分析：

1.最好情况分析：时间复杂度为O(nlog2n)

如果初始数据序列随机分布，使得每次划分恰好分为两个长度相同的子表，此时递归树的高度最小，性能最好

2.最坏情况分析：时间复杂度为O(n^2)

如果初始数据序列正序或者反序，使得每次划分的两个子表中一个为空一个长度为n-1，此时递归树的高度最高，性能最差。

3.平均情况分析：时间复杂度为O(nlog2n)

选择排序：

 简单选择排序：

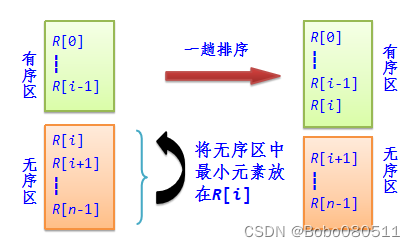
从一个无序区中选出最小的元素，最简单方法是逐个进行元素比较，例如，从无序区R[i..n-1]中选出最小元素R[minj]。

void SelectSort(vector<int>& R,int n)	//简单选择排序
{  for (int i=0;i<n-1;i++)	//做第i趟排序
   {  int minj=i;
      //在当前无序区R[i..n-1]中选最小元素R[minj]
      for (int j=i+1;j<n;j++)	
         if (R[j]<R[minj])
            minj=j;		//minj记下目前找到的最小元素的位置

      if (minj!=i)		//若R[minj]不是无序区首元素
         swap(R[i],R[minj]);	//交换R[i]和R[minj]
   }
}

算法分析：

 无论初始数据序列的状态如何，在第i趟排序从无序区R[i..n-1]（含n-i个元素）中选出最小元素时，内for循环需做n-i-1次比较，因此，总的比较次数为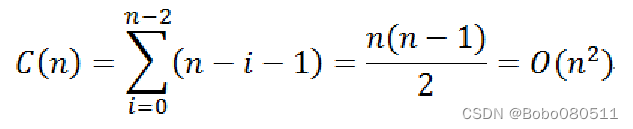

当初始数据序列正序时，元素的移动次数为0。反序时每趟排序均要执行交换操作，此时总的移动次数为最大值3(n-1)。最好、最坏和平均情况的时间复杂度均为O(n^2)。

是一种不稳定的排序方法。

---

堆排序：采用堆方法选出最大元素

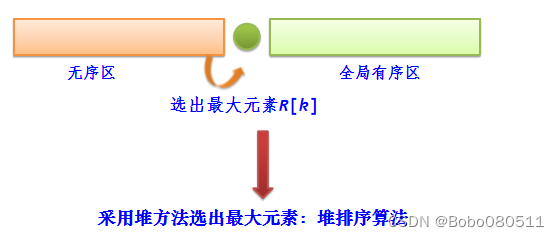
堆的定义：一个序列R[0..n-1]，关键字分别为k0、k1、……、kn-1。

该序列满足如下性质（简称为堆性质）：
   小根堆：ki≤k2i+1 且 ki≤k2i+2   
   大根堆：ki≥k2i+1 且 ki≥k2i+2    （0≤i≤[n/2]-1）

堆的数据结构：

template <typename T>
class Heap			//堆数据结构的实现(默认大根堆)
{  int n;			//堆中元素个数
   vector<T> R;		//用R[0..n-1]存放堆中元素
public:
   Heap():n(0) {}		//构造函数

   void push(T e)				//插入元素e
  { 
    n++;					//堆中元素个数增1
    if (R.size()>=n)			//R中有多余空间
      R[n-1]=e;
    else					//R中没有多余空间
      R.push_back(e); 		//将e添加到末尾
  
    if (n==1) return;			//e作为根结点的情况
    int j=n-1;
    siftUp(j);				//从叶子结点R[j]向上筛选
  }

    T pop()				//删除堆顶元素
   {  if (n==1)
      {  n=0;
      return R[0];
      }

     T e=R[0];			//取出堆顶元素
     R[0]=R[n-1];		//用尾元素覆盖R[0]
     n--;				//元素个数减少1
     siftDown(0,n-1);		//筛选为一个堆
     return e;
  }

    T gettop()	//取堆顶元素
  {
    return R[0];
  }

   bool empty()	//判断堆是否为空
  {
   return n==0;
  }

1.将序列a0 a1 … an-1看成是一颗完全二叉树

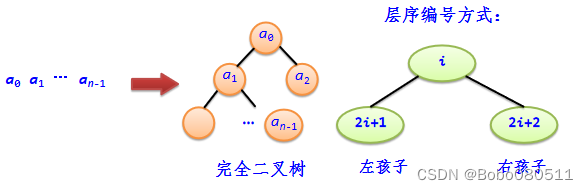
 大根堆：对应的完全二叉树中，任意一个结点的关键字都大于或等于它的孩子结点的关键字。最小关键字的元素一定是某个叶子结点！！！

2.如何判断一颗完全二叉树是否为大根堆

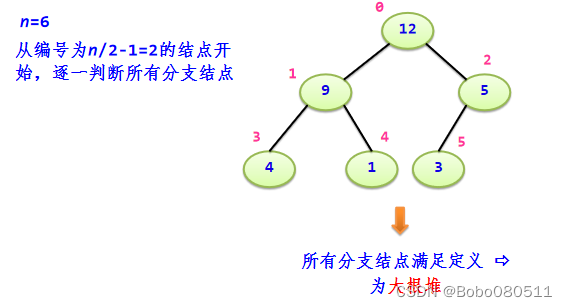
 排序算法：

堆排序的关键是构造堆，这里采用筛选算法建堆。

所谓“筛选”指的是，对一棵左/右子树均为堆的完全二叉树，“调整”根结点使整个二叉树也成为一个堆

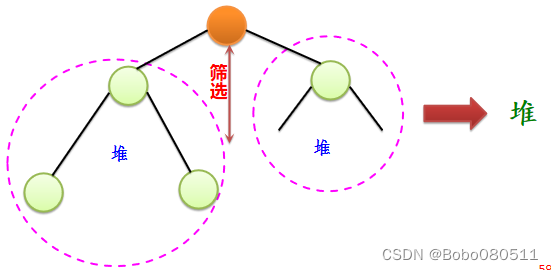
 1. 筛选：不是堆 → 堆

自顶向下筛选：从根结点R[low]开始向下依次查找较大的孩子结点，构成一个序列（2，9，4），其中除了2外其他元素的子序列恰好是递减的。采用类似直接插入排序的思路使其成为一个递减序列（因为大根堆中从根到每个叶子结点的路径均构成一个递减序列）。

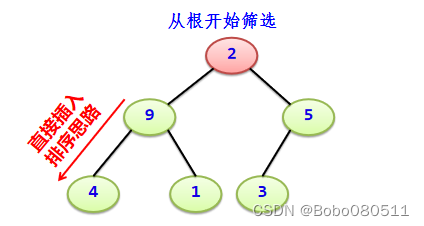
仅仅处理从根结点到某个叶子结点路径上的结点。n个结点的完全二叉树高度为[log2(n+1)]。
所有筛选的时间复杂度为O(log2n)

向下筛选算法：

void siftDown(vector<int>& R,int low,int high)
//R[low..high]的自顶向下筛选
{  int i=low;
   int j=2*i+1;			//R[j]是R[i]的左孩子
   int tmp=R[i];			//tmp临时保存根结点

   while (j<=high)			//只对R[low..high]的元素进行筛选
   {  if (j<high && R[j]<R[j+1])
         j++;				//若右孩子较大,把j指向右孩子

      if (tmp<R[j]) 			//tmp的孩子较大
      {  R[i]=R[j];			//将R[j]调整到双亲位置上
         i=j; j=2*i+1;		//修改i和j值,以便继续向下筛选
      }
      else break;			//若孩子较小，则筛选结束
   }

   R[i]=tmp;				//原根结点放入最终位置
}

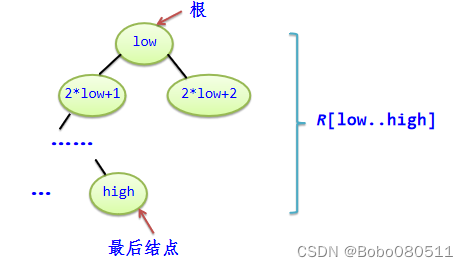
 向上筛选算法：

void siftUp(vector<int>& R,int j)  //自底向上筛选:从叶子结点j向上筛选
{  
   int i=(j-1)/2; 		      //i指向R[j]的双亲

   while (true)
   {  if (R[j]>R[i])		      //若孩子较大
         swap(R[i],R[j]);	      //交换

      if (i==0) break;	      //到达根结点时结束

      j=i;
      i=(j-1)/2;		      //继续向上调整
   }
}

2.一颗完全二叉树  → 初始堆

采用向下筛选算法。

for (int i=n/2-1;i>=0;i--)		     
         //从最后一个分支结点开始循环建立初始堆
   siftDown(R,i,n-1);			
	//对R[i..n-1]进行筛选

3.最大元素归位

 堆排序算法：

void HeapSort(vector<int>& R,int n)	//堆排序
{  for (int i=n/2-1;i>=0;i--)	//从最后一个分支结点开始循环建立初始堆
      siftDown(R,i,n-1);		//对R[i..n-1]进行筛选

   for (int i=n-1;i>0;i--)	//进行n-1趟排序,每一趟后无序区元素个数减1
   {  swap(R[0],R[i]);	//将无序区中尾元素与R[0]交换，扩大有序区
      siftDown(R,0,i-1);		//对无序区R[0..i-1]继续筛选
   }
}

算法分析：

对高度为h的堆，一次“筛选”所需进行的关键字比较的次数至多为2(h-1)。

对n个关键字，建成高度为h（=[log2n]+1）的堆，所需进行的关键字比较的次数不超过4n。

堆排序的时间复杂度为O(nlog2n)。空间复杂度为O(1)，不稳定。

---

归并排序

自底而上的二路归并排序→归并树

有清晰的趟数（同一趟产生的归并段优先归并）。归并树高度h=[log2n]+1。归并的趟数=h-1

1.二路归并算法：将两个位置相邻的有序子序列归并为一个有序序列。

void Merge(vector<int>& R,int low,int mid,int high)
//将R[low..mid]和R[mid+1..high]两个有序段归并为一个有序段R[low..high]
{  vector<int> R1;
   R1.resize(high-low+1);	    //设置R1的长度为high-low+1
   int i=low,j=mid+1,k=0;	   //k是R1的下标,i、j分别为第1、2段的下标

   while (i<=mid && j<=high)	    //在第1段和第2段均未扫描完时循环
   {  if (R[i]<=R[j])		    //将第1段中的元素放入R1中
      {  R1[k]=R[i];
         i++; k++;
      }
      else			    //将第2段中的元素放入R1中
      {  R1[k]=R[j];
         j++; k++; 
      }
   }

   while (i<=mid)		    //将第1段余下部分复制到R1
   {  R1[k]=R[i];
      i++; k++;
   }

   while (j<=high)		    //将第2段余下部分复制到R1
   {  R1[k]=R[j];
      j++; k++;
   }

   for (k=0,i=low;i<=high;k++,i++) //将R1复制回R中
      R[i]=R1[k];
}

2.一趟二路归并排序

有序子表长度为len→R[0..n-1]中共分为[n/len]个有序的子表

void MergePass(vector<int>& R,int length)	
//对整个数序进行一趟归并
{  int n=R.size(),i;
   for (i=0; i+2*length-1<n; i+=2*length) //归并length长的两相邻子表
       Merge(R, i, i+length-1, i+2*length-1);

   if (i+length<n)			//余下两个子表,后者长度小于length
       Merge(R, i, i+length-1, n-1);	//归并这两个子表
}

3.二路归并排序

void MergeSort1(vector<int>& R,int n) 	//自底向上的二路归并排序
{  for (int length=1; length<n; length=2*length) //进行log2n趟归并
     MergePass(R,length);
}

算法分析：

二路归并排序中，长度为n的排序表需做[log2n]趟，对应的归并树高度为log2n，每趟归并时间为O(n)。时间复杂度的最好、最坏和平均情况都是O(nlog2n)。

归并排序过程中每次调用Merge都需要使用局部数组R1，但执行完后其空间被释放，但最后一趟排序一定是全部n个元素参与归并，所以总的辅助空间复杂度为O(n)。

三路归并的归并树的高度为[log3n]，同样一次三路归并的时间为O(n)，所以三路归并排序的时间复杂度为O(nlog3n)。
而nlog3n=nlog2n/log23，即O(nlog3n)=O(nlog2n)，也就是说，三路归并排序与二路归并排序的时间复杂度相同。

自顶而下的二路归并排序：

void MergeSort2(vector<int>& R,int n)  //自顶向下的二路归并排序
{
   _MergeSort2(R,0,n-1);
}

void _MergeSort2(vector<int>& R,int s,int t) //被MergeSort2调用
{  if (s>=t) return;			//R[s..t]的长度为0或者1时返回
   int m=(s+t)/2;			//取中间位置m
   _MergeSort2(R,s,m);		//对前子表排序
   _MergeSort2(R,m+1,t);		//对后子表排序
   Merge(R,s,m,t);			//将两个有序子表合并成一个有序表
}

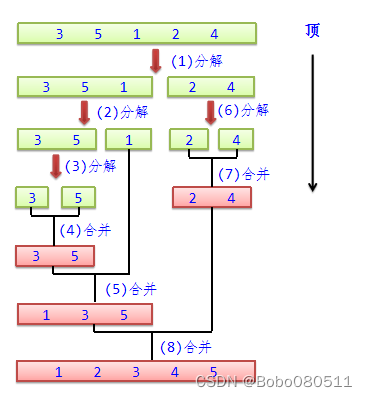
 算法分析：

时间复杂度：

空间复杂度：

---

基数排序：一种借助于多关键字排序的思想对单关键字排序的方法。

所谓多关键字是指讨论元素中含有多个关键字，假设多个关键字分别为k1、k2、…、kd，称k1是第一关键字，kd是第d个关键字。
基数排序就是利用多关键字排序思路，只不过将元素中的单个关键字分为多个位，每个位看成一个关键字。

一般地，在基数排序中元素R[i]的关键字R[i].key是由d位数字组成，即kd-1kd-2…k0，每一个数字表示关键字的一位，其中kd-1为最高位，k0是最低位，每一位的值都在0≤ki<r范围内，其中，r称为基数。
例如，对于二进制数r为2，对于十进制数r为10。
假设kd-1是最重要位，k0是最不重要位，应该从最低位开始排序，称为最低位优先（LSD）。
若kd-1是最不重要位，k0是最重要位，应该从最高位开始排序，称为最高位优先（MSD）。

最低位优先排序：

假设线性表由元素序列a0、a1、…、an-1构成，每个结点aj的关键字由d元组构成。其中每个元素值在0到r-1之间。排序中使用r个队列Q0，Q1，…，Qr-1。

对i=0、1、…，d-1（从低位到高位），依次做一次“分配”和“收集”：

分配：开始时，把Q0、Q1、…、Qr-1各个队列置成空队列，然后依次考察线性表中的每一个元素aj（j=1、2、…、n），如果aj的关键字位   =k，就把aj插入到Qk队列中。

收集：将Q0、Q1、…、Qr-1各个队列中的元素依次首尾相接，得到新的元素序列，从而组成新的线性表。

排序算法：

由于在分配和收集中涉及大量元素移动，采用顺序表时效率较低，所以采用单链表存放排序序列，这里采用以h为首结点的单链表（不带头结点）。

template <typename T>
struct LinkNode			//单链表结点类型
{  T data;				//存放数据元素
   LinkNode<T>* next;			//指向下一个结点的域
   LinkNode():next(NULL) {}		//构造函数 
   LinkNode(T d):data(d),next(NULL) {} //重载构造函数 
};

int geti(int key,int r,int i)	  //求基数为r的正整数key的第i位
{  int k=0;
   for (int j=0;j<=i;j++)
   {  k=key%r;
      key=key/r;
   }
   return k;
}

void RadixSort1(LinkList<int>& L,int d,int r)
//最低位优先基数排序算法
{  LinkNode<int>* front[MAXR];	//建立链队队头数组
   LinkNode<int>* rear[MAXR];		//建立链队队尾数组
   LinkNode<int>* p,*t;
   for (int i=0;i<d;i++)		//从低位到高位循环
   {  for (int j=0;j<r;j++)		//初始化各链队首、尾指针
         front[j]=rear[j]=NULL;
      p=L.head->next;
      while (p!=NULL)			//分配：对于原链表中每个结点循环
      {  int k=geti(p->data,r,i); //提取关键字第k个位并放入第k个链队
         if (front[k]==NULL)	     //第k个链队空时，队头队尾均指向p结点
         {  front[k]=p;
            rear[k]=p;
         }
         else				//第k个链队非空时，p结点进队
         {  rear[k]->next=p;
            rear[k]=p;
         }
         p=p->next;			//取下一个待排序的结点
     }
  LinkNode<int>* h=NULL;	//重新用h来收集所有结点
   for (int j=0;j<r;j++)	//收集：对于每一个链队循环
      if (front[j]!=NULL)	//若第j个链队是第一个非空链队
      {  if (h==NULL)
         {  h=front[j];
            t=rear[j];
         }
         else			//若第j个链队是其他非空链队
         {  t->next=front[j];
            t=rear[j];
         }
      }
      t->next=NULL;		//尾结点的next域置NULL
      L.head->next=h;
   }
}

算法分析：分配为O(n)。收集为O(r)（r为“基数”）。d为“分配-收集”的趟数

 基数排序的时间复杂度为O(d(n+r))。基数排序的空间复杂度为O(r)