欧拉路径和欧拉回路基本概念和模板题

前言：

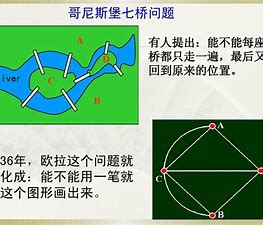
 上图可以得出引出两个概念：

欧拉路径：在一个连通图里面每条边都只走一次且走完所有边的路径。

欧拉回路：在一个连通图里面从一个起点出发，每条边只走一次并且最后回到终点的一个回路。

欧拉回路是包含在欧拉路径里面的，只要欧拉路径的起点和终点是同一个点就是欧拉回路。

在一个欧拉路径里面，要有起点和终点，现在先看起点和终点是不同点的情形：

起点：起点最开始会有一条边1用于走出去，如果后面又通过一条边2走了回来，那么一定会通过一条边3走出去，由此可得，起点所连的边的数量一定是奇数。

终点：终点在最后会有一条没走过的边n可以进去，其余情况下进去和出去都要从别的两个条边进出，由此可得，终点连的边的数量也是奇数。

其他：其余非起点终点的点连的边都是偶数条。

欧拉回路：起点终点都是同一个点时就要保证所有点的数量都是偶数。

在七桥问题里面有四个点，度数分别是3,3,3,5,不满足只有两个奇数度数或者0个奇数度数的要求，所以是无解的。

结论：

前提，图是连通的

1.对于无向图

(1)存在欧拉路径的充分必要条件：度数为奇数的点只能有0个或者2个

(1)存在欧拉回路的充分必要条件：度数为奇数的点只能是0个

2.对于有向图

(1)存在欧拉路径的充分必要条件：所有点的入度等于出度；或者起点的的出度比入度多1，终点的入度比出度多1，其余点入度等于出度。

(2)存在欧拉回路的充分必要条件：所有点的入度等于出度

以下模板是经过删边优化之后的：

该优化的作用，在深搜的时候当第一次枚举到i这条边时，这条边就已经会被入队了，但是搜索树上层的节点可能还会枚举到这条边，但是因为这条边已经被标记过了，所以不会将它入队，但是还会顺着这条边接着搜索，但是在下层的时候这条边的所有边都已经被搜索完了，这里相当于是在做无用功，最后时间复杂度最差是O(M*M)，要是被卡必定超时。

所以需要对这个算法进行优化，一个可行的方案就是在第一次到达某条边的时候就直接将这条边删除，然后还是顺着这条边原来的方向往下搜索，因为一共就m条边，删除m次就没了，最后时间复杂度会降到O(m)级别。

求无向图欧拉回路模板：

void dfs(int u)
{
    for(int &i=h[u];~i;)
    {
        if(st[i])
        {
            i=ne[i];
            continue;
        }
        st[i^1]=true;

         int tmp;
        tmp=i/2+1;
        if(i&1) tmp=-tmp;//反向边
        int j=e[i];
        i=ne[i];
        dfs(j);
       
        ans[++cnt]=tmp;
    }
}

求有向图欧拉回路模板：

void dfs(int u)
{
    for(int &i=h[u];~i;)
    {
        int tmp=i+1;
        
        int j=e[i];
        i=ne[i];
        dfs(j);
        ans[++cnt]=tmp;
    }
}

传送门：欧拉回路

思路：

题目分为两种情况，有向图和无向图。

无向图的话为了保证有解必须要一个点的度数都是偶数。

有向图的话要保证每个点的入度等于出度。

另外，还有一个大前提就是该图是连通的。

代码：

#include <iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cmath>
using namespace std;
typedef pair<int ,int>PII;
const int N=1e5+10,M=4e5+10;
int e[M],ne[M],h[N],idx;
int n,m;
bool st[M]; //记录该边有没有被用过
int ans[M],cnt;
int din[N],dout[N];
int t;
void add(int a,int b)
{
    e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
void dfs(int u)
{
    for(int &i=h[u];~i;)//让i
    {
        if(st[i]) //在无向图里面需要进行额外的对反向边的查重，如果当前邻边已经被用过
        {
            i=ne[i];  //删除该边，这里这条边被标记了却没被删除是因为这条边是反向边
            continue;
        }
        st[i]=true; //如果还没遍历过，接下来也会立刻用到，所以也要标记
        if(t==1) st[i^1]=true;//无向图就要连反向边也标记

        int tmp;//记录该点是第几条边
        if(t==1)  
        {
            tmp=i/2+1;  //无向图的话因为是两条边同时建的所以(0,1)算第一条边，(2,3)算第二条
            if(i&1) tmp=-tmp; //在无向图下如果i是奇数说明是反向边，就要输出负数的编号
        }else tmp=i+1;  //有向图的话编号加1即可，因为idx是从0开始，题目从1开始
 
        int j=e[i]; //保留完当前边之后在把当前边删除
        i=ne[i]; 
        
        dfs(j); //从当前接着往下搜索。
        
         ans[++cnt]=tmp;//在加完该点后面的所有边之后将该边入队。
    }
}
int main()
{
    scanf("%d",&t);
    memset(h,-1,sizeof h);
    scanf("%d%d",&n,&m);
    for(int i=0;i<m;i++)
    {
        int a,b;
        scanf("%d%d",&a,&b);
        add(a,b);
        if(t==1) //无向图就建个反向边
        add(b,a);
        din[b]++,dout[a]++;
    }
    if(t==1)
    {
        for(int i=1;i<=n;i++)
            if((din[i] + dout[i])%2) //无向图里面有某个点的度数为奇数
        {
            printf("NO\n");
            return 0;
        }
    }else
    {
        for(int i=1;i<=n;i++)
            if(din[i]!=dout[i]) //有向图存在一个点的入度和出度不相等
        {
            printf("NO\n");
            return 0;
        }
    }
    for(int i=1;i<=n;i++)//为了满足连通性，要从一个非孤点进去
        if(h[i]!=-1)
    {
        dfs(i);
        break;
    }
    if(cnt<m) //最后得到的边的数量小于图中边的数量则不连通
    {
        puts("NO");
        return 0;
    }
    puts("YES");
    for(int i=cnt;i;i--)
        printf("%d ",ans[i]);
        puts("");
    return 0;
}

拆开有向和无向用两个函数求的模板：

#include <iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cmath>
using namespace std;
typedef pair<int ,int>PII;
const int N=1e5+10,M=4e5+10;
int e[M],ne[M],h[N],idx;
int n,m;
bool st[M]; //记录该边有没有被用过
int ans[M],cnt;
int din[N],dout[N];
int t;
void add(int a,int b)
{
    e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
void dfs1(int u) //处理无向图的
{
    for(int &i=h[u];~i;)
    {
        if(st[i])
        {
            i=ne[i];
            continue;
        }
        st[i^1]=true;

         int tmp;
        tmp=i/2+1;
        if(i&1) tmp=-tmp;//反向边
        int j=e[i];
        i=ne[i];
        dfs1(j);
       
        ans[++cnt]=tmp;
    }
}
void dfs(int u) //处理有向图的
{
    for(int &i=h[u];~i;)
    {
        int tmp=i+1;
        
        int j=e[i];
        i=ne[i];
        dfs(j);
        ans[++cnt]=tmp;
    }
}
int main()
{
       scanf("%d",&t);
    memset(h,-1,sizeof h);
    scanf("%d%d",&n,&m);
    for(int i=0;i<m;i++)
    {
        int a,b;
        scanf("%d%d",&a,&b);
        add(a,b);
        if(t==1)
        add(b,a);
        din[b]++,dout[a]++;
    }
    if(t==1)
    {
        for(int i=1;i<=n;i++)
            if((din[i] + dout[i])%2)
        {
            printf("NO\n");
            return 0;
        }
    }else
    {
        for(int i=1;i<=n;i++)
            if(din[i]!=dout[i]) //有向图存在一个点的入度和出度不相等
        {
            printf("NO\n");
            return 0;
        }
    }
    for(int i=1;i<=n;i++)//为了满足连通性，要从一个非孤点进去
        if(h[i]!=-1)
    {
        if(t==2)
        dfs(i);
        else
        dfs1(i);
        break;
    }
    if(cnt<m) //最后得到的边的数量小于图中边的数量则无解
    {
        puts("NO");
        return 0;
    }
    puts("YES");
    for(int i=cnt;i;i--)
        printf("%d ",ans[i]);
        puts("");
    return 0;
}