计算机图形学实验——二维变换&三维变换

目录

第一部分：实验报告

一、实验目的

二、实验环境

三、实验步骤/过程

（一）全局变量、所用类与所用函数的设计

1. 全局变量（二维变换）

2. 全局变量（三维变换）

3. Matrix矩阵类

4. 项目内除主函数以外的其他函数

（二）二维变换

1. 二维基本变换

2. 二维复合变换

（三）系统整体设计

（四）三维变换

1. 存储三维物体的数据结构

2. 三维物体的绘制

3. 整体逻辑

四、实验结果

1. 二维变换（蓝色为变换前的图形，绿色为变换后的图形）

(1) 基本二维变换

(2) 复合二维变换

2. 三维变换

(1) 基本三维变换（橙色为变换前的图形，蓝色为变换后的图形）

(2) 复合三维变换

第二部分：源代码

1. 二维变换

2. 三维变换

---

第一部分：实验报告

一、实验目的

1. 通过实验，进一步理解和掌握二维基本几何变换的基本原理，理解和掌握二维复合变换（即：相对于任一点或任一方向的变换）的基本原理；

2. 掌握在C/C++编程环境下（或其它环境）实现对二维模型的基本几何变换和复合变换。

二、实验环境

OS：Windows 10

IDE：Microsoft Visual Studio Community 2022 (64 位) – Current

程序基于OpenGL编写

三、实验步骤/过程

（一）全局变量、所用类与所用函数的设计

1. 全局变量（二维变换）

变量类型	变量名	含义
int	Vertexnum	多边形点个数
Matrix	PolygonMatrix	多边形坐标矩阵
Matrix	AnsMatrix	变换后坐标矩阵

2. 全局变量（三维变换）

变量类型	变量名	含义
**GLfloat	OriginalVertexes	三维物体变换前坐标
**GLfloat	FinalVertexes	三维物体变换后坐标
**int	FacesId	立方体每个面由哪些点（点下标）构成
Matrix	PolygonMatrix	三维物体坐标矩阵
Matrix	AnsMatrix	变换后坐标矩阵

3. Matrix矩阵类

Private私有成员：

变量类型	变量名	含义
int	rownum	矩阵行数
int	colnum	矩阵列数
**float	matrix	存储矩阵

Public公有成员：

函数声明	含义
Matrix()	默认空构造函数
Matrix( int r, int c )	构造r*c的零矩阵
void IdentityMatrix()	化成单位矩阵
int getRowNum()	返回矩阵行数
int getColNum()	返回矩阵列数
void setElement( int r, int c, float value )	设定矩阵中位于(r, c)元素的值为value
float getElement( int r, int c )	返回矩阵中位于(r, c)元素的值
void plusElement( int r, int c, float value )	矩阵中位于(r, c)元素的值追加value
void print()	输出矩阵
void input()	键入矩阵各个元素的值
void copy3_3( Matrix matrix )	复制3*3矩阵
void copy4_4( Matrix matrix )	复制4*4矩阵
void build( int row, int col )	对于未被构建的矩阵，构建为row*col的零矩阵
void Multiply( Matrix right, Matrix &ans )	this与right进行矩阵乘法，结果赋给ans
void Movement2( float dx = 0, float dy = 0 )	二维基本变换 -- 平移
void Scaletrans2( float Sx = 1, float Sy = 1 )	二维基本变换 -- 比例变换
void Rotate2( float theta )	二维基本变换 -- 旋转
void Symmetry2( int choice )	二维基本变换 -- 对称（choice选定对称类型）
void Shear2( float thetaX = 0, float thetaY = 0 )	二维基本变换 -- 错切变换
void Movement3( float dx = 0, float dy = 0, float dz = 0 )	三维基本变换 -- 平移
void Scaletrans3( float Sx = 1, float Sy = 1, float Sz = 1 )	三维基本变换 -- 比例变换
void RotateZ3( float theta )	三维基本变换 -- 绕Z轴旋转
void RotateX3( float theta )	三维基本变换 -- 绕X轴旋转
void RotateY3( float theta )	三维基本变换 -- 绕Y轴旋转
void Symmetry3( int choice )	三维基本变换 -- 对称（choice选定对称类型）

4. 项目内除主函数以外的其他函数

函数声明	含义
void SelectBasicTrans2( Matrix &matrix, int choice )	choice选择基本二维变换，matrix为变换矩阵
void CompositeTrans2( Matrix &matrix )	二维复合变换，matrix为复合变换后最终的矩阵
void SelectBasicTrans3( Matrix &matrix, int choice )	choice选择基本三维变换，matrix为变换矩阵
void CompositeTrans3( Matrix &matrix )	三维复合变换，matrix为复合变换后最终的矩阵
void initPolygon()	图形矩阵初始化（仅对于三维变换）
void saveVertexes()	将变换后的点保存到FianlVertexes中（仅对于三维变换）
void mainProcess()	主进程，输入/选定相关数据（二维三维的不一样）
void paintGL()	绘制函数（二维三维的不一样）
void init()	OpenGL初始化（仅在二维变换中）

（二）二维变换

1. 二维基本变换

每一种基本变换都对应着一种矩阵，只要知道了变换时的相关数据就知道了这个矩阵。下面以平移变换为例介绍这一过程。

对于某一个图形，将它沿x轴方向平移 ∆x 个单位，沿y轴方向平移 ∆y 个单位。定义一个变换矩阵matrix，设定为单位矩阵。根据上面的平移变换矩阵 T ，可知设定matrix的第3行第1列元素为 ∆x ，第3行第2列元素为 ∆y 后即可得到。同理，我们可以得到其他基本变换的变换矩阵。

2. 二维复合变换

有两种复合变换形式：相对于任一点的变换和相对于任一方向的变换。为了便于编程，可以将这两种变换统一为后面一种形式。对于某一个图形，相对于AB方向做某些基本变换，当A、B点坐标相同时，即变为相对于某一点的变换。另外，在相对于AB方向（A、B不重合时）做诸如旋转、缩放等变换时，以A、B中最低点（y值最小）为相对点做相应变换。

T=T平移∙T旋转∙T相对变换1∙T相对变换2∙…  ∙T相对变换 n∙T反旋转∙T反平移

根据上面的论述，我们可以总结出二维复合变换中变换矩阵的统一形式（如上式）。对于某一个图形，相对于AB方向做n个基本变换。当A、B不重合时，找到A、B中的最低点，将最低点平移到原点，得到A’、B’，随后将OB’旋转到坐标轴（如x轴）上；此时依次进行n个相对变换；最后经过反旋转、反平移操作，恢复到最初的情况。当A、B重合时，问题就转变为了相对于某一点的变换，然后将这一点平移到原点；因为两点重合旋转与反旋转矩阵都是单位矩阵；随后依次进行n个相对变换；最后经过反旋转、反平移操作，恢复到最初的情况。

（三）系统整体设计

系统整体执行逻辑如下。

(1) mainProcess()： 输入多边形的点数和各个点的坐标，初始化多边形点坐标矩阵，选择变换类型。

(2)[选择基本变换] SelectBasicTrans2()：根据刚才选择的基本变换类型，调用相应的Matrix类内基本变换函数，获得变换矩阵。

(2)[选择复合变换]  CompositeTrans2()：输入相对AB方向的A、B点坐标，据此获得平移、反平移、旋转、反旋转矩阵。输入复合变换中基本变换的个数，依次选择（SelectBasicTrans2()）并进行变换，每次都将上一个（最初为单位矩阵）与此次变换矩阵相乘。最后，根据前文推导出来的公式，依次将矩阵相乘，获得最终的变换矩阵。

(3) 回到mainProcess()，将多边形点坐标矩阵与刚才获得的变换矩阵相乘，获得变换后的坐标矩阵。

(4) paintGL()：开始绘图。首先绘制坐标轴，然后根据最初的多边形点坐标矩阵绘制出变换前图形，最后根据变换后的坐标矩阵绘制出变换后图形。

（四）三维变换

相应操作大致与二维变换一致，与后者相比多了几个参数；另外，此时该使用部分后缀带“3”的函数。下面主要介绍一些与二维变换操作的不同点。

1. 存储三维物体的数据结构

对于三维物体，除了基本的点坐标信息，还需要边信息，这时候沿用二维变换的操作就不太行了。参考某博客，获知可以通过设计两个二维数组来存储，前者存储点信息（下图中的OriginalVertexes），后者存储每个面由哪几个点组成（下图中的FacesId）。

 

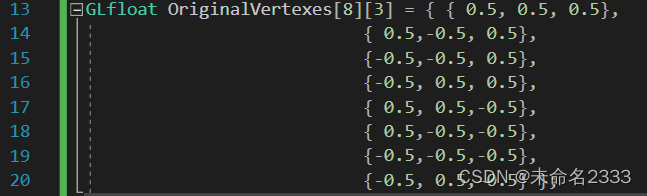
2. 三维物体的绘制

下面以绘制立方体为例介绍此过程。参考某博客，首先需要使用gluLookAt()设定观察者视角。随后绘制立方体的面，遍历FacesId，据此再通过OriginalVertexes找到所确定每个面的点坐标，代码如下所示。

    glBegin( GL_QUADS );

    for ( int i = 0; i < 6; i++ )

           for ( int j = 0; j < 4; j++ ) {

                  glVertex3f( OriginalVertexes[FacesId[i][j]][0], OriginalVertexes[FacesId[i][j]][1], OriginalVertexes[FacesId[i][j]][2] );

           }

    glEnd();

绘制立方体的边。这里会有一个问题，每个面有4个点和4条边，但每条边要用两个点来确定，所以在绘制时要与其（位置，同时这里也是坐标）相邻的点配对来确定边。代码如下所示。

    glBegin( GL_LINES );

    for ( int i = 0; i < 6; i++ )

           for ( int j = 0; j < 4; j++ ) {

                  glVertex3f( OriginalVertexes[FacesId[i][j]][0], OriginalVertexes[FacesId[i][j]][1], OriginalVertexes[FacesId[i][j]][2] );

                  glVertex3f( OriginalVertexes[FacesId[i][( j + 3 ) % 4]][0], OriginalVertexes[FacesId[i][( j + 3 ) % 4]][1], OriginalVertexes[FacesId[i][( j + 3 ) % 4]][2] );

           }

    glEnd();

3. 整体逻辑

基本的逻辑和二维复合变换相同，不同的是这里需要先使用initPolygon()初始化，读取OriginalVertexes，将点坐标放到PolygonMatrix；后面也需要类似的操作，将变换后的点使用saveVertexes()保存到FinalVertexes中；在最后绘图时，是按照OriginalVertexes与FinalVertexes绘图，而不是根据坐标矩阵。

四、实验结果

1. 二维变换（蓝色为变换前的图形，绿色为变换后的图形）

(1) 基本二维变换

① 平移

② 比例变换

③ 旋转

④ 对称

关于原点对称：

关于y=-x对称：

⑤ 错切

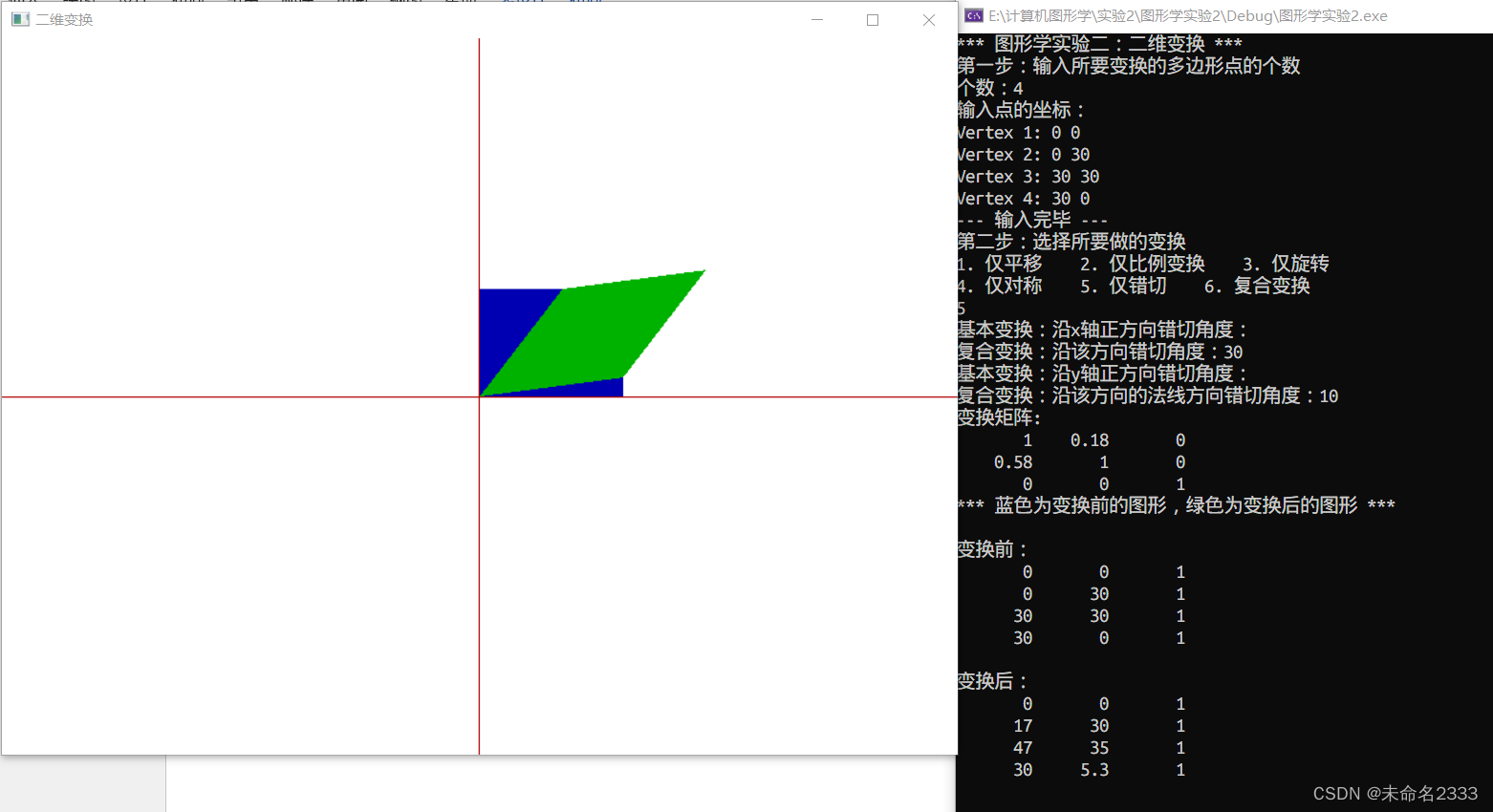
(2) 复合二维变换

① 相对于(80, -80)做1次旋转20度的变换。

② 相对于A(10, 15)、B(70, 45)两点所确定直线的经过最低点（A）的法线的对称变换。

③ 相对于A(10, 15)、B(70, 45)两点所确定直线做一次平移变换，沿AB平移-50，沿AB法线方向平移-70；相对于AB做对称变换。

第一步结果：

 

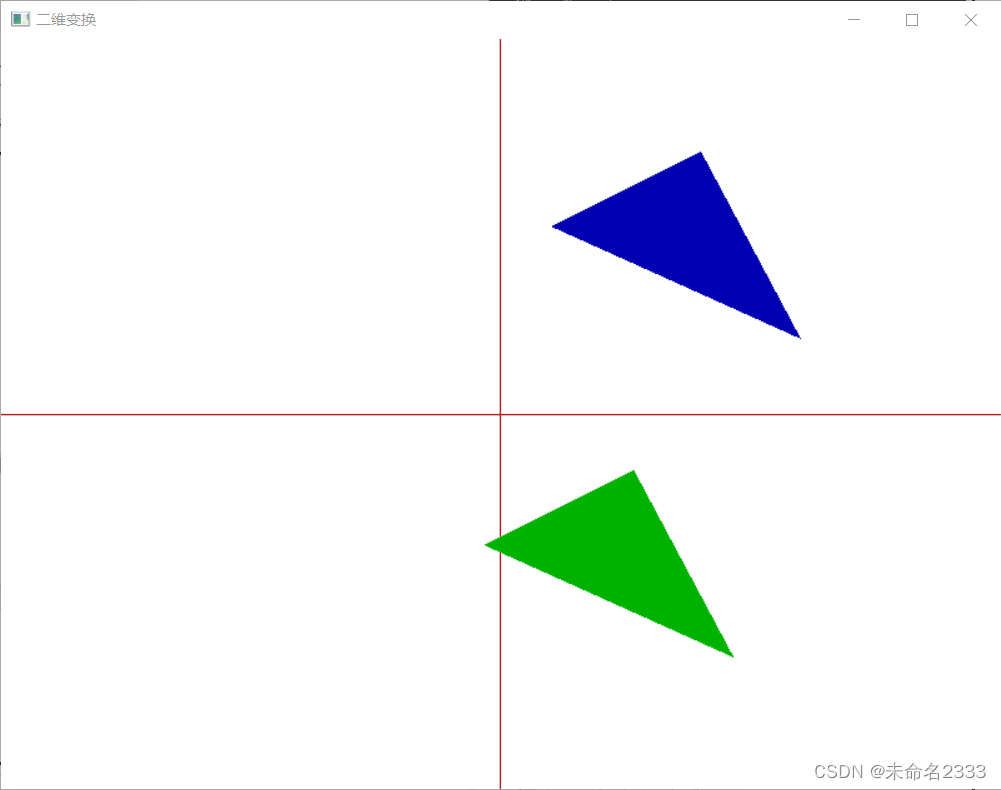
最终结果：

2. 三维变换

(1) 基本三维变换（橙色为变换前的图形，蓝色为变换后的图形）

① 平移

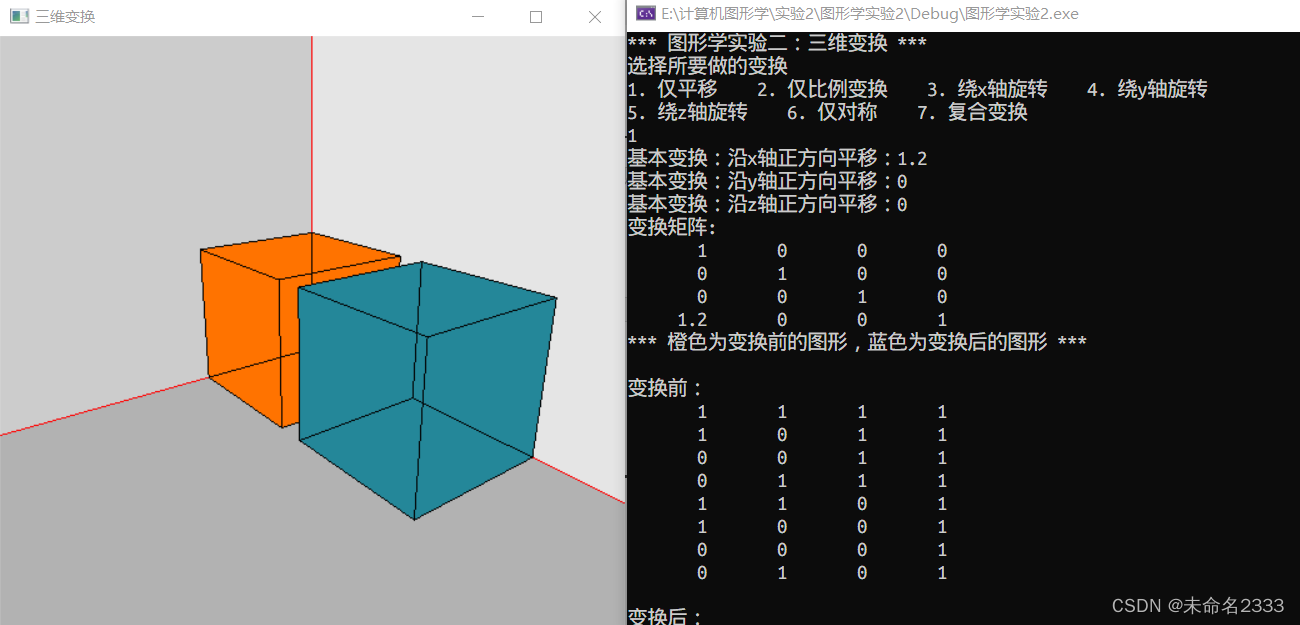
② 比例变换

③ 绕x轴旋转

④ 绕y轴旋转

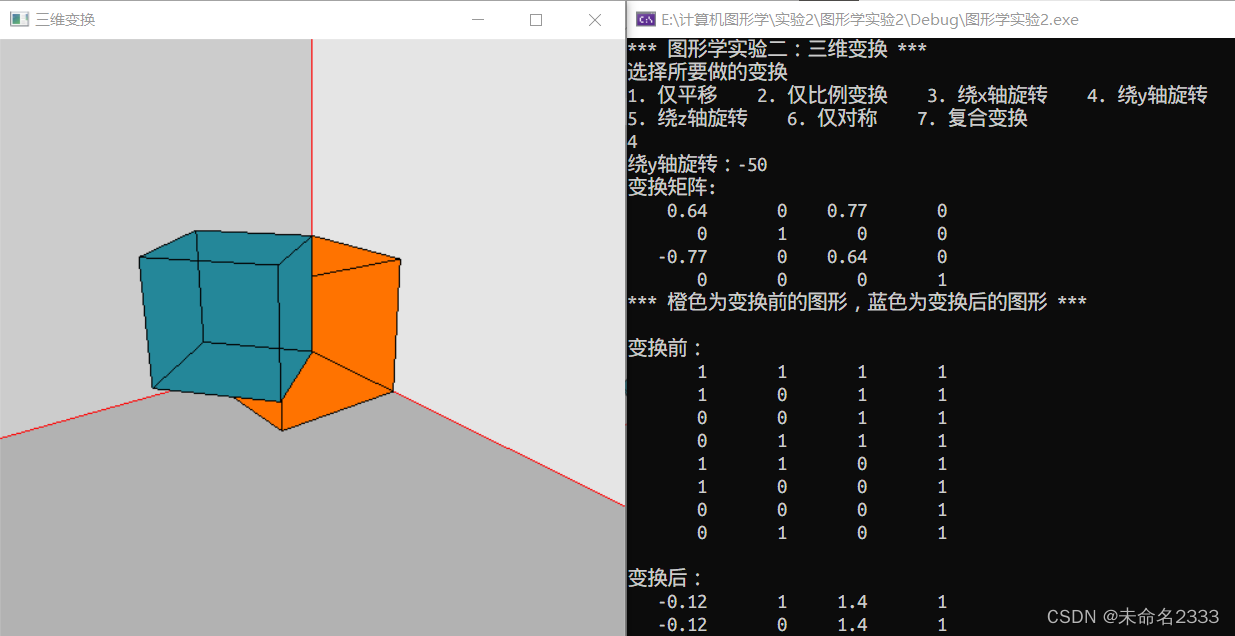
⑤ 绕z轴旋转

⑥ 关于xoy面对称

(2) 复合三维变换

先沿A(0, 0, 0)、B(1, 1, 1)直线方向平移0.5，随后绕AB旋转30度。

第一步结果：

最终结果：

第二部分：源代码

1. 二维变换

// 图形学实验2.cpp : 此文件包含 "main" 函数。程序执行将在此处开始并结束。

#include <GL/glut.h>
#include <iostream>
#include <cmath>
#include <iomanip>
#include "windows.h"
using namespace std;

// 矩阵类
class Matrix
{
private:
	int rownum = 0;
	int colnum = 0;
	float **matrix;
public:
	// 默认空构造函数
	Matrix() {

	}

	// 默认构造 3*3 的零矩阵
	//Matrix() {
	//	rownum = colnum = 3;
	//	matrix = new float *[rownum];
	//	for ( int i = 0 ; i < rownum; i++ )
	//		matrix[i] = new float[colnum];
	//	for ( int i = 0; i < rownum; i++ )
	//		for ( int j = 0; j < colnum; j++ )
	//			matrix[i][j] = 0;
	//}

	// 构造 r*c 的零矩阵
	Matrix( int r, int c ) {
		rownum = r;
		colnum = c;
		matrix = new float *[rownum];
		for ( int i = 0 ; i < rownum; i++ )
			matrix[i] = new float[colnum];
		for ( int i = 0; i < rownum; i++ )
			for ( int j = 0; j < colnum; j++ )
				matrix[i][j] = 0;
	}

	// 化为单位矩阵
	void IdentityMatrix() {
		for ( int i = 0; i < rownum; i++ )
			for ( int j = 0; j < colnum; j++ )
				if ( i == j )
					matrix[i][j] = 1;
				else
					matrix[i][j] = 0;
	}

	int getRowNum() {
		return rownum;
	}

	int getColNum() {
		return colnum;
	}

	void setElement( int r, int c, float value ) {
		matrix[r][c] = value;
	}

	float getElement( int r, int c ) {
		return matrix[r][c];
	}

	void plusElement( int r, int c, float value ) {
		matrix[r][c] += value;
	}

	void print() {
		for ( int i = 0; i < rownum; i++ ) {
			for ( int j = 0; j < colnum; j++ ) {
				cout << right << setw( 8 ) << setprecision( 2 ) << matrix[i][j];
			}
			cout << endl;
		}
	}

	// 3*3 矩阵复制
	void copy3_3( Matrix matrix ) {
		for ( int i = 0; i < 3; i++ )
			for ( int j = 0; j < 3; j++ )
				this->setElement( i, j, matrix.getElement( i, j ) );
	}

	void input() {
		for ( int i = 0; i < rownum; i++ )
			for ( int j = 0; j < colnum; j++ )
				cin >> matrix[i][j];
	}

	// 矩阵置空
	void setEmpty() {
		for ( int i = 0; i < rownum; i++ )
			for ( int j = 0; j < colnum; j++ )
				matrix[i][j] = 0;
	}

	// 矩阵构建 (对于未构造的Matrix对象)
	void build( int row, int col ) {
		rownum = row;
		colnum = col;
		matrix = new float *[rownum];
		for ( int i = 0 ; i < rownum; i++ )
			matrix[i] = new float[colnum];
		for ( int i = 0; i < rownum; i++ )
			for ( int j = 0; j < colnum; j++ )
				matrix[i][j] = 0;
	}

	// 矩阵乘法
	Matrix Multiply( Matrix right ) {
		int ansrow = this->getRowNum();
		int anscol = right.getColNum();
		int same = this->getColNum();
		Matrix ans( ansrow, anscol );
		for ( int i = 0; i < ansrow; i++ )
			for ( int j = 0; j < anscol; j++ )
				for ( int k = 0; k < same; k++ ) {
					ans.plusElement( i, j, this->getElement( i, k ) * right.getElement( k, j ) );
				}
		return ans;
	}

	// 矩阵乘法
	void Multiply( Matrix right, Matrix &ans ) {
		int ansrow = this->getRowNum();
		int anscol = right.getColNum();
		int same = this->getColNum();
		for ( int i = 0; i < ansrow; i++ )
			for ( int j = 0; j < anscol; j++ )
				for ( int k = 0; k < same; k++ ) {
					ans.plusElement( i, j, this->getElement( i, k ) * right.getElement( k, j ) );
				}
	}

	// 二维基本变换 -- 平移
	void Movement2( float dx = 0, float dy = 0 ) {
		this->IdentityMatrix();
		this->setElement( 2, 0, dx );
		this->setElement( 2, 1, dy );
	}

	// 二维基本变换 -- 比例变换
	void Scaletrans2( float Sx = 1, float Sy = 1 ) {
		this->IdentityMatrix();
		this->setElement( 0, 0, Sx );
		this->setElement( 1, 1, Sy );
	}

	// 二维基本变换 -- 旋转
	void Rotate2( float theta ) {
		this->IdentityMatrix();
		this->setElement( 0, 0, cos( theta ) );
		this->setElement( 0, 1, sin( theta ) );
		this->setElement( 1, 0, -sin( theta ) );
		this->setElement( 1, 1, cos( theta ) );
	}

	// 二维基本变换 -- 对称
	void Symmetry2( int choice ) {
		switch ( choice ) {
			// 关于x轴对称
			case 1: {
					this->IdentityMatrix();
					this->setElement( 1, 1, -1 );
					break;
				}
				  // 关于y轴对称
			case 2: {
					this->IdentityMatrix();
					this->setElement( 0, 0, -1 );
					break;
				}
				  // 关于原点对称
			case 3: {
					this->IdentityMatrix();
					this->setElement( 0, 0, -1 );
					this->setElement( 1, 1, -1 );
					break;
				}
				  // 关于y=x对称
			case 4: {
					this->setEmpty();
					this->setElement( 0, 1, 1 );
					this->setElement( 1, 0, 1 );
					this->setElement( 2, 2, 1 );
					break;
				}
				  // 关于y=-x对称
			case 5: {
					this->setEmpty();
					this->setElement( 0, 1, -1 );
					this->setElement( 1, 0, -1 );
					this->setElement( 2, 2, 1 );
					break;
				}
		}
	}

	// 二维基本变换 -- 错切变换
	void Shear2( float thetaX = 0, float thetaY = 0 ) {
		this->IdentityMatrix();
		this->setElement( 1, 0, tan( thetaX ) );
		this->setElement( 0, 1, tan( thetaY ) );
	}
};


// 全局变量 -- 多边形点个数
int Vertexnum = 0;
// 全局变量 -- 多边形矩阵 & 变换后矩阵
Matrix PolygonMatrix, AnsMatrix;


// 选择基本二维变换
void SelectBasicTrans2( Matrix &matrix, int choice ) {
	switch ( choice ) {
		case 1: {
				float dx = 0, dy = 0;
				cout << "基本变换：沿x轴正方向平移：\n复合变换：沿该方向平移：";
				cin >> dx;
				cout << "基本变换：沿y轴正方向平移：\n复合变换：沿该方向的法线方向平移：";
				cin >> dy;
				matrix.Movement2( dx, dy );
				break;
			}
		case 2: {
				float Sx = 1, Sy = 1;
				cout << "基本变换：沿x方向放缩：\n复合变换：沿该方向放缩：";
				cin >> Sx;
				cout << "基本变换：沿y方向放缩：\n复合变换：沿该方向的法线方向放缩：";
				cin >> Sy;
				matrix.Scaletrans2( Sx, Sy );
				break;
			}
		case 3: {
				float theta;
				cout << "基本变换：绕原点逆时针旋转（角度）：\n复合变换：绕最低点逆时针旋转（角度）：";
				cin >> theta;
				matrix.Rotate2( theta * 3.1415 / 180 );
				break;
			}
		case 4: {
				cout << "选择基本变换的对称类型（对于复合变换，x轴为设定方向，y轴为设定方向的经过最低点的法线方向）：\n1. 关于x轴对称    2. 关于y轴对称   3. 关于原点对称\n4. 关于y=x对称    5. 关于y=-x对称" << endl;
				int type = 0;
				cin >> type;
				matrix.Symmetry2( type );
				break;
			}
		case 5: {
				float thetaX, thetaY;
				cout << "基本变换：沿x轴正方向错切角度：\n复合变换：沿该方向错切角度：";
				cin >> thetaX;
				cout << "基本变换：沿y轴正方向错切角度：\n复合变换：沿该方向的法线方向错切角度：";
				cin >> thetaY;
				matrix.Shear2( thetaX * 3.1415 / 180, thetaY * 3.1415 / 180 );
				break;
			}
	}
}

// 二维复合变换
void CompositeTrans2( Matrix &matrix ) {
	cout << "该多边形相对于AB方向（A、B重合是相对于A点）做二维几何变换，输入A、B点坐标：\nA点：";
	float ax = 0, ay = 0, bx = 0, by = 0;
	float bottomPointX = 0, bottomPointY = 0;	// 最低点坐标，将其移到原点
	float topPointX = 0, topPointY = 0;	// 最高点坐标
	cin >> ax >> ay;
	cout << "B点：";
	cin >> bx >> by;
	if ( ay < by ) {
		bottomPointX = ax;
		bottomPointY = ay;
		topPointX = bx;
		topPointY = by;
	}
	else {
		bottomPointX = bx;
		bottomPointY = by;
		topPointX = ax;
		topPointY = ay;
	}

	Matrix Movement( 3, 3 ), AntiMovement( 3, 3 );	// 平移与反平移矩阵
	Matrix Rotate( 3, 3 ), AntiRotate( 3, 3 );	// 旋转与反旋转矩阵
	Movement.Movement2( -bottomPointX, -bottomPointY );
	AntiMovement.Movement2( bottomPointX, bottomPointY );
	float theta = ( topPointX - bottomPointX == 0 ) ? 0 : atan( ( topPointY - bottomPointY ) / ( topPointX - bottomPointX ) );
	Rotate.Rotate2( -theta );
	AntiRotate.Rotate2( theta );

	int times = 0;	// 基本变换次数
	cout << "输入基本变换次数：";
	cin >> times;

	matrix.IdentityMatrix();
	Matrix temp1( 3, 3 ), temp2( 3, 3 );
	for ( int i = 0; i < times; i++ ) {
		cout << "********************" << endl;
		cout << "第 " << i + 1 << " 次基本变换，选择本次变换的具体操作：\n1. 平移    2. 比例变换    3. 旋转\n4. 对称    5. 错切" << endl;
		cout << "********************" << endl;
		int choice = 0;
		cin >> choice;
		SelectBasicTrans2( temp1, choice );
		matrix.Multiply( temp1, temp2 );
		matrix.copy3_3( temp2 );

		temp1.setEmpty();
		temp2.setEmpty();
	}

	temp1.setEmpty();
	temp2.setEmpty();
	Movement.Multiply( Rotate, temp1 );

	temp1.Multiply( matrix, temp2 );

	temp1.setEmpty();
	temp2.Multiply( AntiRotate, temp1 );

	matrix.setEmpty();
	temp1.Multiply( AntiMovement, matrix );		// 给matrix赋最终值


}

// 绘制函数
void paintGL()
{
	glClear( GL_COLOR_BUFFER_BIT );//清除颜色缓冲区
	glPointSize( 1 );//一个点占据1个像素

	// 坐标轴
	glColor3f( 0.7, 0.0, 0.0 );
	glBegin( GL_LINES );
	glVertex2f( -100.0, 0 );
	glVertex2f( 100.0, 0 );
	glVertex2f( 0, 100.0 );
	glVertex2f( 0, -100.0 );
	glEnd();

	// 绘制变换前的图形
	glColor3f( 0.0, 0.0, 0.7 );
	glBegin( GL_POLYGON );
	for ( int i = 0; i < Vertexnum; i++ ) {
		glVertex2f( PolygonMatrix.getElement( i, 0 ), PolygonMatrix.getElement( i, 1 ) );
	}
	glEnd();

	// 绘制变换后的图形
	glColor3f( 0.0, 0.7, 0.0 );
	glBegin( GL_POLYGON );
	for ( int i = 0; i < Vertexnum; i++ ) {
		glVertex2f( AnsMatrix.getElement( i, 0 ), AnsMatrix.getElement( i, 1 ) );
	}
	glEnd();

	glFlush();//缓存，必不可少，使图像显示
}

// 主进程
void mainProcess()
{
	cout << "*** 图形学实验二：二维变换 ***" << endl;
	cout << "第一步：输入所要变换的多边形点的个数" << endl;
	cout << "个数：";
	cin >> Vertexnum;
	PolygonMatrix.build( Vertexnum, 3 );
	AnsMatrix.build( Vertexnum, 3 );
	cout << "输入点的坐标：" << endl;
	for ( int i = 0; i < Vertexnum; i++ ) {
		cout << "Vertex " << i + 1 << ": ";
		int x, y;
		cin >> x >> y;
		PolygonMatrix.setElement( i, 0, x );
		PolygonMatrix.setElement( i, 1, y );
		PolygonMatrix.setElement( i, 2, 1 );
	}
	cout << "--- 输入完毕 ---" << endl;
	cout << "第二步：选择所要做的变换" << endl;
	cout << "1. 仅平移    2. 仅比例变换    3. 仅旋转\n4. 仅对称    5. 仅错切    6. 复合变换" << endl;
	Matrix matrix( 3, 3 );
	matrix.IdentityMatrix();
	int choice = 0;
	cin >> choice;
	choice == 6 ? CompositeTrans2( matrix ) : SelectBasicTrans2( matrix, choice );

	cout << "变换矩阵:" << endl;
	matrix.print();

	// 变换前后的数据比较
	cout << "*** 蓝色为变换前的图形，绿色为变换后的图形 ***" << endl;
	PolygonMatrix.Multiply( matrix, AnsMatrix );
	cout << "\n变换前：" << endl;
	PolygonMatrix.print();
	cout << endl;
	cout << "变换后：" << endl;
	AnsMatrix.print();
	cout << endl << endl;
}

// 初始化
void init() {
	glClearColor( 1.0, 1.0, 1.0, 0.0 );	//设置背景颜色
	glMatrixMode( GL_PROJECTION );		//正投影方式
	glLoadIdentity();
	gluOrtho2D( -100, 100, -100, 100 );		//设置坐标范围
}


int main( int argc, char *argv[] )
{
	glutInit( &argc, argv );
	glutInitDisplayMode( GLUT_RGB | GLUT_SINGLE );
	glutInitWindowPosition( 100, 100 );
	glutInitWindowSize( 800, 600 );
	glutCreateWindow( "二维变换" );

	mainProcess();
	init();
	glutDisplayFunc( paintGL );

	glutMainLoop();
	return 0;
}

2. 三维变换

// Reference：
// https://www.cnblogs.com/zhengwin7/p/5294161.html
// https://blog.csdn.net/qq_21043585/article/details/125814145

#include <GL/glut.h>
#include <math.h>
#include <vector>
#include <iostream>
#include <iomanip>
using namespace std;

//立方体顶点
//GLfloat OriginalVertexes[8][3] = { { 0.5, 0.5, 0.5},
//                           { 0.5,-0.5, 0.5},
//                           {-0.5,-0.5, 0.5},
//                           {-0.5, 0.5, 0.5},
//                           { 0.5, 0.5,-0.5},
//                           { 0.5,-0.5,-0.5},
//                           {-0.5,-0.5,-0.5},
//                           {-0.5, 0.5,-0.5} };
GLfloat OriginalVertexes[8][3] = { { 1.0, 1.0, 1.0},
						   { 1.0,0.0, 1.0},
						   {0.0,0.0, 1.0},
						   {0.0, 1.0, 1.0},
						   { 1.0, 1.0,0.0},
						   { 1.0,0.0,0.0},
						   {0,0,0},
						   {0, 1.0,0} };

// 变换后顶点
GLfloat FinalVertexes[8][3];

//立方体六个面
int FacesId[6][4] = { { 0, 1, 2, 3},
					{ 4, 5, 6, 7},
					{ 0, 4, 7, 3},
					{ 1, 5, 6, 2},
					{ 0, 4, 5, 1},
					{ 3, 7, 6, 2} };

// 矩阵类
class Matrix
{
private:
	int rownum = 0;
	int colnum = 0;
	float **matrix;
public:
	// 默认空构造函数
	Matrix() {

	}

	// 构造 r*c 的零矩阵
	Matrix( int r, int c ) {
		rownum = r;
		colnum = c;
		matrix = new float *[rownum];
		for ( int i = 0 ; i < rownum; i++ )
			matrix[i] = new float[colnum];
		for ( int i = 0; i < rownum; i++ )
			for ( int j = 0; j < colnum; j++ )
				matrix[i][j] = 0;
	}

	// 化为单位矩阵
	void IdentityMatrix() {
		for ( int i = 0; i < rownum; i++ )
			for ( int j = 0; j < colnum; j++ )
				if ( i == j )
					matrix[i][j] = 1;
				else
					matrix[i][j] = 0;
	}

	int getRowNum() {
		return rownum;
	}

	int getColNum() {
		return colnum;
	}

	void setElement( int r, int c, float value ) {
		matrix[r][c] = value;
	}

	float getElement( int r, int c ) {
		return matrix[r][c];
	}

	void plusElement( int r, int c, float value ) {
		matrix[r][c] += value;
	}

	void print() {
		for ( int i = 0; i < rownum; i++ ) {
			for ( int j = 0; j < colnum; j++ ) {
				cout << right << setw( 8 ) << setprecision( 2 ) << matrix[i][j];
			}
			cout << endl;
		}
	}

	void input() {
		for ( int i = 0; i < rownum; i++ )
			for ( int j = 0; j < colnum; j++ )
				cin >> matrix[i][j];
	}

	// 4*4 矩阵复制
	void copy4_4( Matrix matrix ) {
		for ( int i = 0; i < 4; i++ )
			for ( int j = 0; j < 4; j++ )
				this->setElement( i, j, matrix.getElement( i, j ) );
	}

	// 矩阵置空
	void setEmpty() {
		for ( int i = 0; i < rownum; i++ )
			for ( int j = 0; j < colnum; j++ )
				matrix[i][j] = 0;
	}

	// 矩阵构建 (对于未构造的Matrix对象)
	void build( int row, int col ) {
		rownum = row;
		colnum = col;
		matrix = new float *[rownum];
		for ( int i = 0 ; i < rownum; i++ )
			matrix[i] = new float[colnum];
		for ( int i = 0; i < rownum; i++ )
			for ( int j = 0; j < colnum; j++ )
				matrix[i][j] = 0;
	}

	// 矩阵乘法
	Matrix Multiply( Matrix right ) {
		int ansrow = this->getRowNum();
		int anscol = right.getColNum();
		int same = this->getColNum();
		Matrix ans( ansrow, anscol );
		for ( int i = 0; i < ansrow; i++ )
			for ( int j = 0; j < anscol; j++ )
				for ( int k = 0; k < same; k++ ) {
					ans.plusElement( i, j, this->getElement( i, k ) * right.getElement( k, j ) );
				}
		return ans;
	}

	// 矩阵乘法
	void Multiply( Matrix right, Matrix &ans ) {
		int ansrow = this->getRowNum();
		int anscol = right.getColNum();
		int same = this->getColNum();
		for ( int i = 0; i < ansrow; i++ )
			for ( int j = 0; j < anscol; j++ )
				for ( int k = 0; k < same; k++ ) {
					ans.plusElement( i, j, this->getElement( i, k ) * right.getElement( k, j ) );
				}
	}

	// 三维基本变换 -- 平移
	void Movement3( float dx = 0, float dy = 0, float dz = 0 ) {
		this->IdentityMatrix();
		this->setElement( 3, 0, dx );
		this->setElement( 3, 1, dy );
		this->setElement( 3, 2, dz );
	}

	// 三维基本变换 -- 比例变换
	void Scaletrans3( float Sx = 1, float Sy = 1, float Sz = 1 ) {
		this->IdentityMatrix();
		this->setElement( 0, 0, Sx );
		this->setElement( 1, 1, Sy );
		this->setElement( 2, 2, Sz );
	}

	// 三维基本变换 -- 绕Z轴旋转
	void RotateZ3( float theta ) {
		this->IdentityMatrix();
		this->setElement( 0, 0, cos( theta ) );
		this->setElement( 0, 1, sin( theta ) );
		this->setElement( 1, 0, -sin( theta ) );
		this->setElement( 1, 1, cos( theta ) );
	}

	// 三维基本变换 -- 绕X轴旋转
	void RotateX3( float theta ) {
		this->IdentityMatrix();
		this->setElement( 1, 1, cos( theta ) );
		this->setElement( 1, 2, sin( theta ) );
		this->setElement( 2, 1, -sin( theta ) );
		this->setElement( 2, 2, cos( theta ) );
	}

	// 三维基本变换 -- 绕Y轴旋转
	void RotateY3( float theta ) {
		this->IdentityMatrix();
		this->setElement( 0, 0, cos( theta ) );
		this->setElement( 2, 0, sin( theta ) );
		this->setElement( 0, 2, -sin( theta ) );
		this->setElement( 2, 2, cos( theta ) );
	}

	// 三维基本变换 -- 对称
	void Symmetry3( int choice ) {
		switch ( choice ) {
			// 关于xoy平面对称
			case 1: {
					this->IdentityMatrix();
					this->setElement( 2, 2, -1 );
					break;
				}
				  // 关于yoz平面对称
			case 2: {
					this->IdentityMatrix();
					this->setElement( 0, 0, -1 );
					break;
				}
				  // 关于xoz平面对称
			case 3: {
					this->IdentityMatrix();
					this->setElement( 1, 1, -1 );
					break;
				}
				  // 关于x轴对称
			case 4: {
					this->IdentityMatrix();
					this->setElement( 1, 1, -1 );
					this->setElement( 2, 2, -1 );
					break;
				}
				  // 关于y轴对称
			case 5: {
					this->IdentityMatrix();
					this->setElement( 0, 0, -1 );
					this->setElement( 2, 2, -1 );
					break;
				}
				  // 关于z轴对称
			case 6: {
					this->IdentityMatrix();
					this->setElement( 1, 1, -1 );
					this->setElement( 0, 0, -1 );
					break;
				}
		}
	}
};

// 选择基本三维变换
void SelectBasicTrans3( Matrix &matrix, int choice ) {
	switch ( choice ) {
		case 1: {
				float dx = 0, dy = 0, dz = 0;
				cout << "基本变换：沿x轴正方向平移：";
				cin >> dx;
				cout << "基本变换：沿y轴正方向平移：";
				cin >> dy;
				cout << "基本变换：沿z轴正方向平移：";
				cin >> dz;
				matrix.Movement3( dx, dy, dz );
				break;
			}
		case 2: {
				float Sx = 1, Sy = 1, Sz = 1;
				cout << "基本变换：沿x方向放缩：";
				cin >> Sx;
				cout << "基本变换：沿y方向放缩：";
				cin >> Sy;
				cout << "基本变换：沿z方向放缩：";
				cin >> Sz;
				matrix.Scaletrans3( Sx, Sy, Sz );
				break;
			}
		case 3: {
				float theta;
				cout << "绕x轴旋转：";
				cin >> theta;
				matrix.RotateX3( theta * 3.1415 / 180 );
				break;
			}
		case 4: {
				float theta;
				cout << "绕y轴旋转：";
				cin >> theta;
				matrix.RotateY3( theta * 3.1415 / 180 );
				break;
			}
		case 5: {
				float theta;
				cout << "绕z轴旋转：";
				cin >> theta;
				matrix.RotateZ3( theta * 3.1415 / 180 );
				break;
			}
		case 6: {
				cout << "选择基本变换的对称类型：\n1. 关于xoy面对称    2. 关于yoz面对称   3. 关于xoz面对称\n4. 关于x轴对称    5. 关于y轴对称    6. 关于z轴对称" << endl;
				int type = 0;
				cin >> type;
				matrix.Symmetry3( type );
				break;
			}
	}
}

// 三维复合变换
void CompositeTrans3( Matrix &matrix ) {
	cout << "该多边形相对于AB方向（A、B重合是相对于A点）做三维几何变换，输入A、B点坐标：\nA点：";
	float ax = 0, ay = 0, az = 0, bx = 0, by = 0, bz = 0;
	float bottomPointX = 0, bottomPointY = 0, bottomPointZ = 0;	// 最低点坐标，将其移到原点
	float topPointX = 0, topPointY = 0, topPointZ = 0;	// 最高点坐标
	cin >> ax >> ay >> az;
	cout << "B点：";
	cin >> bx >> by >> bz;
	if ( ay < by ) {
		bottomPointX = ax;
		bottomPointY = ay;
		bottomPointZ = az;
		topPointX = bx;
		topPointY = by;
		topPointZ = bz;
	}
	else {
		bottomPointX = bx;
		bottomPointY = by;
		bottomPointZ = bz;
		topPointX = ax;
		topPointY = ay;
		topPointZ = az;
	}

	Matrix Movement( 4, 4 ), AntiMovement( 4, 4 );	// 平移与反平移矩阵
	Matrix RotateX( 4, 4 ), AntiRotateX( 4, 4 );	// 旋转与反旋转矩阵 (绕X轴)
	Matrix RotateY( 4, 4 ), AntiRotateY( 4, 4 );	// 旋转与反旋转矩阵 (绕Y轴)
	Movement.Movement3( -bottomPointX, -bottomPointY, -bottomPointZ );
	AntiMovement.Movement3( bottomPointX, bottomPointY, bottomPointZ );
	
	float alpha = ( topPointY - bottomPointY == 0 ) ? 0 : atan( ( topPointX - bottomPointX ) / ( topPointX - bottomPointX ) );
	float v = sqrt( ( topPointX - bottomPointX ) * ( topPointX - bottomPointX ) + ( topPointX - bottomPointX ) * ( topPointX - bottomPointX ) );
	float beta = ( v == 0 ) ? 0 : atan( ( topPointZ - bottomPointZ ) / v );

	RotateX.RotateX3( alpha );
	AntiRotateX.RotateX3( -alpha );
	RotateY.RotateY3( -beta );
	AntiRotateY.RotateY3( beta );

	int times = 0;	// 基本变换次数
	cout << "输入基本变换次数：";
	cin >> times;

	matrix.IdentityMatrix();
	Matrix temp1( 4, 4 ), temp2( 4, 4 );
	for ( int i = 0; i < times; i++ ) {
		cout << "********************" << endl;
		cout << "第 " << i + 1 << " 次基本变换，选择本次变换的具体操作：\n1. 平移    2. 比例变换   5. 绕轴旋转    6. 对称" << endl;
		cout << "********************" << endl;
		int choice = 0;
		cin >> choice;
		SelectBasicTrans3( temp1, choice );

		matrix.Multiply( temp1, temp2 );
		matrix.copy4_4( temp2 );

		temp1.setEmpty();
		temp2.setEmpty();
	}

	temp1.setEmpty();
	temp2.setEmpty();
	Movement.Multiply( RotateX, temp1 );

	temp1.Multiply( RotateY, temp2 );

	temp1.setEmpty();
	temp2.Multiply( matrix, temp1 );

	temp2.setEmpty();
	temp1.Multiply( AntiRotateY, temp2 );

	temp1.setEmpty();
	temp2.Multiply( AntiRotateX, temp1 );

	matrix.setEmpty();
	temp1.Multiply( AntiMovement, matrix );		// 给matrix赋最终值
}

// 全局变量 -- 多边形矩阵 & 变换后矩阵
Matrix PolygonMatrix( 8, 4 ), AnsMatrix( 8, 4 );

// 图形矩阵初始化
void initPolygon() {
	for ( int i = 0; i < 8; i++ ) {
		for ( int j = 0; j < 3; j++ ) {
			PolygonMatrix.setElement( i, j, OriginalVertexes[i][j] );
		}
		PolygonMatrix.setElement( i, 3, 1 );
	}
}

// 将变换后的点保存到FinalVertexes中
void saveVertexes() {
	for ( int i = 0; i < 8; i++ )
		for ( int j = 0; j < 3; j++ )
			FinalVertexes[i][j] = AnsMatrix.getElement( i, j );
}

// 主进程
void mainProcess()
{
	cout << "*** 图形学实验二：三维变换 ***" << endl;
	cout << "选择所要做的变换" << endl;
	cout << "1. 仅平移    2. 仅比例变换    3. 绕x轴旋转    4. 绕y轴旋转\n5. 绕z轴旋转    6. 仅对称    7. 复合变换" << endl;
	initPolygon();
	Matrix matrix( 4, 4 );
	matrix.IdentityMatrix();
	int choice = 0;
	cin >> choice;
	choice == 7 ? CompositeTrans3( matrix ) : SelectBasicTrans3( matrix, choice );

	cout << "变换矩阵:" << endl;
	matrix.print();

	// 变换前后的数据比较
	cout << "*** 橙色为变换前的图形，蓝色为变换后的图形 ***" << endl;
	PolygonMatrix.Multiply( matrix, AnsMatrix );
	cout << "\n变换前：" << endl;
	PolygonMatrix.print();
	cout << endl;
	cout << "变换后：" << endl;
	AnsMatrix.print();
	cout << endl << endl;

	saveVertexes();
}


void paintGL( void ) {
	glClearColor( 1.0, 1.0, 1.0, 0.0 );
	glClear( GL_COLOR_BUFFER_BIT );
	glLoadIdentity();
	gluLookAt( 4.0, 2.0, 3.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0 );

	// 绘制坐标轴与坐标平面
	// xoy面（右）：
	glColor3f( 0.9, 0.9, 0.9 );
	glBegin( GL_QUADS );
	glVertex3f( 0, 0, 0 );
	glVertex3f( 0, 100, 0 );
	glVertex3f( 100, 100, 0 );
	glVertex3f( 100, 0, 0 );
	glEnd();
	// yoz面（左）：
	glColor3f( 0.80, 0.80, 0.80 );
	glBegin( GL_QUADS );
	glVertex3f( 0, 0, 0 );
	glVertex3f( 0, 100, 0 );
	glVertex3f( 0, 100, 100 );
	glVertex3f( 0, 0, 100 );
	// xoz面（下）：
	glColor3f( 0.7, 0.7, 0.7 );
	glBegin( GL_QUADS );
	glVertex3f( 0, 0, 0 );
	glVertex3f( 100, 0, 0 );
	glVertex3f( 100, 0, 100 );
	glVertex3f( 0, 0, 100 );
	glEnd();

	// 坐标轴线
	glColor3f( 1, 0, 0 );
	glBegin( GL_LINES );
	glVertex3f( 0, 0, 0 );
	glVertex3f( 100, 0, 0 );
	glVertex3f( 0, 0, 0 );
	glVertex3f( 0, 100, 0 );
	glVertex3f( 0, 0, 0 );
	glVertex3f( 0, 0, 100 );
	glEnd();

	// 绘制原立方体 -- 面
	glColor3f( 1.0, 0.45, 0 );
	glBegin( GL_QUADS );
	for ( int i = 0; i < 6; i++ )
		for ( int j = 0; j < 4; j++ ) {
			glVertex3f( OriginalVertexes[FacesId[i][j]][0], OriginalVertexes[FacesId[i][j]][1], OriginalVertexes[FacesId[i][j]][2] );
		}
	glEnd();

	// 绘制原立方体 -- 边
	glColor3f( 0.0, 0.0, 0.0 );
	glBegin( GL_LINES );
	for ( int i = 0; i < 6; i++ )
		for ( int j = 0; j < 4; j++ ) {
			glVertex3f( OriginalVertexes[FacesId[i][j]][0], OriginalVertexes[FacesId[i][j]][1], OriginalVertexes[FacesId[i][j]][2] );
			glVertex3f( OriginalVertexes[FacesId[i][( j + 3 ) % 4]][0], OriginalVertexes[FacesId[i][( j + 3 ) % 4]][1], OriginalVertexes[FacesId[i][( j + 3 ) % 4]][2] );
		}
	glEnd();

	// 绘制变换后立方体 -- 面
	glColor3f( 0.14, 0.53, 0.6 );
	glBegin( GL_QUADS );
	for ( int i = 0; i < 6; i++ )
		for ( int j = 0; j < 4; j++ ) {
			glVertex3f( FinalVertexes[FacesId[i][j]][0], FinalVertexes[FacesId[i][j]][1], FinalVertexes[FacesId[i][j]][2] );
		}
	glEnd();

	// 绘制变换后立方体 -- 边
	glColor3f( 0.0, 0.0, 0.0 );
	glBegin( GL_LINES );
	for ( int i = 0; i < 6; i++ )
		for ( int j = 0; j < 4; j++ ) {
			glVertex3f( FinalVertexes[FacesId[i][j]][0], FinalVertexes[FacesId[i][j]][1], FinalVertexes[FacesId[i][j]][2] );
			glVertex3f( FinalVertexes[FacesId[i][( j + 3 ) % 4]][0], FinalVertexes[FacesId[i][( j + 3 ) % 4]][1], FinalVertexes[FacesId[i][( j + 3 ) % 4]][2] );
		}
	glEnd();

	glFlush();
}

void threeD( int w, int h ) {
	glViewport( 0, 0, (GLsizei)w, (GLsizei)h );//调整视图窗口大小
	glMatrixMode( GL_PROJECTION );
	glLoadIdentity();
	glFrustum( -1.0, 1.0, -1.0, 1.0, 2.0, 10.0 );
	glMatrixMode( GL_MODELVIEW );

}

int main( int argc, char *argv[] ) {

	//初始化GLUT library
	glutInit( &argc, argv );
	//对窗口的大小进行初始化
	glutInitWindowSize( 500, 500 );
	// 设置窗口出现的位置
	//glutInitWindowPosition(int x, int y);
	//初始化程序展示模式
	glutInitDisplayMode( GLUT_RGBA );
	glutCreateWindow( "三维变换" );
	mainProcess();
	//为当前窗口设置函数回调，用于画图
	glutDisplayFunc( paintGL );
	//窗口改变时的函数
	glutReshapeFunc( threeD );
	glutMainLoop();

	return 0;
}

---

参考：

https://www.cnblogs.com/zhengwin7/p/5294161.html
https://blog.csdn.net/qq_21043585/article/details/125814145