Acwing 2.01背包问题

温水煮汤圆

已于 2023-03-04 10:21:09 修改

阅读量255

点赞数

分类专栏： Acwing算法题解文章标签：算法

于 2022-10-18 19:43:57 首次发布

本文链接：https://blog.csdn.net/m0_62513791/article/details/127394017

版权

Acwing算法题解专栏收录该内容

6 篇文章 0 订阅

订阅专栏

一、题目

有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。

第 i 件物品的体积是 v[i]，价值是 w[i]。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。

输入格式

第一行两个整数，N，V，用空格隔开，分别表示物品数量和背包容积。

接下来有 N 行，每行两个整数 v[i], w[i]，用空格隔开，分别表示第 i 件物品的体积和价值。

输出格式

输出一个整数，表示最大价值。

数据范围

0<N,V≤1000
0<v[i],w[i]≤1000

输入样例

输出样例：

二、题目解析

1.为什么说是01背包问题？

因为在挑选物品装入书包的过程中，每件物品都有两种选择，要么选要么不选；我们用01来形象的表示物品的选取与不选取。

2.如何理解这道题目？

我们可以先看能明确表示数据规模的关键词，这道题目是我们要从N件物品中选择总体积不超过V的物品，保证总价值最大。那么如果我们能解决它的子问题，即从 i 件物品中选择总体姐不超过 j 的物品且总价值最大的问题，那么我们一定能解决这个问题。

三、解决问题

1.DP图分析

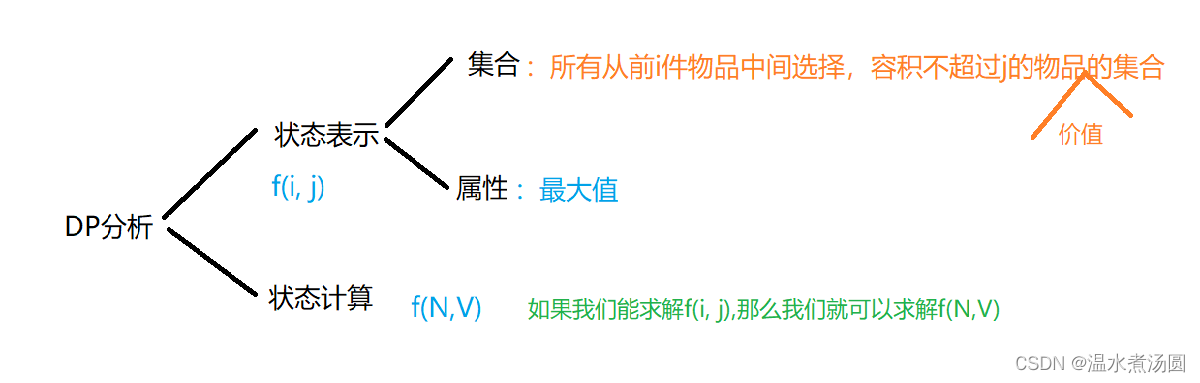
2.那我们如何计算f(i, j)呢（状态转移）？

我们选择从第 i 个物品下手，考虑第 i 个物品的选择情况。如下图：

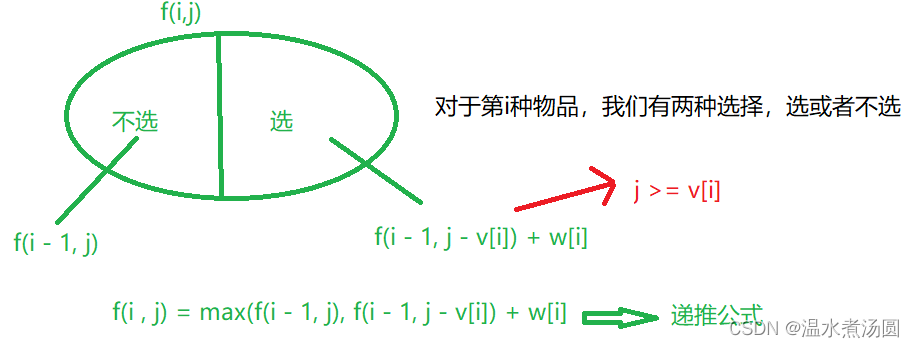
（1）如果我们不选第 i 个物品，那么从前 i 个物品中选择且体积不超过 j 方案，相当于从前 i - 1个物品中选择且体积不超过 j 的方案（这句话要重点理解一下，多看几遍）

（2）如果我们选择第 i 个物品，那么从前 i 个物品中选择且体积不超过 j 方案，相当于从前 i - 1个物品中选择且体积不超过 j - v[i] 的方案（因为只考虑前 i - 1 中的情况，所以我们要先把选择的第 i 个物品的体积刨除掉）

经过上面两步，我们就成功实现了状态转移，将f(i, j)转移到了f(i - 1, j)和f(i - 1, j - v[i])的情况

因为我们要求的是最大值，所以在两种情况中取MAX就好了~

3.初始状态

（1）i == 0时，也就是物品为空，那么对应的 f[0, j] = 0；

（2）j == 0时，也就是体积为空，那么对应的 f[i, 0] = 0；

4.注意

（1）观察上面的状态转移图，由f(i - 1, j - v[i])可知隐藏条件应该是背包的容积要大于物品的体积，这样才能装得下，也就是 j >= v[i]。

（2）f(i , j)是一个状态集合，存储的是每一种情况下的最大价值

（3）注意f(i - 1, j - v[i]) + w[i]，一定要加上物品的价值w[i]，因为f(i, j)里面存储的值是最大价值（分析：f(i - 1, j - v[i]表示的是从前 i - 1中物品中挑选的物品最大价值，因此要想表示f(i, j)的话必须要加上选择的第 i 件物品的价值）

四、代码实现

1.朴素做法

#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[N][N];

int main(){
    cin >> n >> m;
    for(int i = 1; i <= n; i ++) scanf("%d %d", &v[i], &w[i]);
    
    for(int i = 1; i <= n; i ++)
        for(int j = 0; j <= m; j ++)//体积可以从0开始
        {
            f[i][j] = f[i - 1][j];
            if(j >= v[i]) f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
        }
    
    cout << f[n][m] << endl;
    
    return 0;
}

2.滚动数组优化

#include <iostream>
#include <cmath>
#include <algorithm>
using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[N];//一维是在二维的基础上删掉了行方向

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i ++) scanf("%d%d", &v[i], &w[i]);

    for(int i = 1; i <= n; i ++)
    {
        for(int j = m; j >= v[i]; j --)
        {
            //f[i][j] = f[i - 1][j];等价变形为f[j] = f[j];可以直接删掉
            /*if(j >= v[i]) f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);
            等价变形为f[j] = max(f[j], f[j - v[i]]+ w[i],其实与原来的二维等式是不等价的
            因为f[j - v[i]]的值已经被更新过了，不再是原来的旧值，那我们就采取从右到左算*/
            f[j] = max(f[j], f[j - v[i]] + w[i]);
        }
    }

    cout << f[m];

    return 0;
}

五、优化解释

1.为什么可以用滚动数组进行优化？

在计算f(i, j)的过程中，我们发现我们只用到了第 i 行和第 i - 1的数据，顾名思义，我们可以通过持续不断数组滚动来更新第 i 行的数据，即用新的数据覆盖旧的数据，以降低算法的空间复杂度。

2.直接删除一维，看删除前的式子和删除后的式子是否等价？

f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i])删除一维后变成了f[j] = max(f[j], f[j - v[i]] + w[i])，因为f[i][j]是一行一行从前往后计算的，因此f[j - v[i]]一定实在f[j]之前被更新过一遍，而第一个式子中的f[i - 1][j - v[i]是旧值。所以如果遵循从前往后计算的话，这两个式子就不等价了。因此我们的解决办法是：让 j 从大到小开始遍历。