学习吃瓜教程第3章线性模型总结

梦中人z

已于 2024-05-16 12:00:15 修改

阅读量589

点赞数 18

分类专栏：机器学习文章标签：学习机器学习人工智能

于 2024-04-20 19:44:32 首次发布

本文链接：https://blog.csdn.net/m0_62557756/article/details/138006976

版权

机器学习专栏收录该内容

5 篇文章 0 订阅

订阅专栏

本文详细介绍了线性模型（包括线性回归和正规方程推导）、矩阵操作、对数线性回归以及逻辑回归（对数几率回归）的概念和求导过程。特别强调了逻辑回归的对数几率函数和其在多分类问题中的应用，包括线性判别分析和多分类学习方法。文中还提到了相关书籍和资源作为学习参考。

摘要由CSDN通过智能技术生成

1、线性模型

线性模型是试图学习一个通过各种属性的线性组合来进行预测的函数

$f(\boldsymbol{x})=w_1x_1+w_2x_2+\ldots+w_dx_d+b,$

向量的形式是： $f(\boldsymbol{x})=\boldsymbol{w}^\mathrm{T}\boldsymbol{x}+b\mathrm{~}$

线性回归(Linear regression)是利⽤回归⽅程(函数)对⼀个或多个⾃变量(特征值)和 因变量(⽬标值)之间关系进⾏建模的⼀种分析⽅式。

2、矩阵（向量）求导

参考链接：Matrix calculus - Wikipedia

3、正规方程的推导

$\hat{\boldsymbol{w}}^*=\left(\mathbf{X}^\mathrm{T}\mathbf{X}\right)^{-1}\mathbf{X}^\mathrm{T}\boldsymbol{y}$

先从西瓜书均方误差最小化开始： $\begin{aligned} (w^*,b^*)& =\arg\min_{(w,b)}\sum_{i=1}^m\left(f\left(x_i\right)-y_i\right)^2 \\ &=\arg\min_{(w,b)}\sum_{i=1}^m(y_i-wx_i-b)^2. \end{aligned}$

之后在多元线性回归中，我们把w 和 b 吸收入向量形式 $\hat{\boldsymbol{w}}=(\boldsymbol{w};b)$ ,相应的，把数据集D 表示为一个 $m\times(d+1)$ 大小的矩阵X , 其中每行对应于一个示例，该行前d 个元素对应于示例的d 个属性值,最后一个元素恒置为1 ,即

$\begin{gathered}\mathbf{X}=\begin{pmatrix}x_{11}&x_{12}&\ldots&x_{1d}&1\\x_{21}&x_{22}&\ldots&x_{2d}&1\\\vdots&\vdots&\ddots&\vdots&\vdots\\x_{m1}&x_{m2}&\ldots&x_{md}&1\end{pmatrix}=\begin{pmatrix}\boldsymbol{x}_1^\mathrm{T}&1\\\boldsymbol{x}_2^\mathrm{T}&1\\\vdots&\vdots\\\boldsymbol{x}_m^\mathrm{T}&1\end{pmatrix},\end{gathered}$

$\hat{\boldsymbol{w}}*{X}$

故可以得出： $\hat{\boldsymbol{w}}^*=\arg\min_{\hat{\boldsymbol{w}}}\left(\boldsymbol{y}-\mathbf{X}\hat{\boldsymbol{w}}\right)^\mathrm{T}\left(\boldsymbol{y}-\mathbf{X}\hat{\boldsymbol{w}}\right)$ （本来是一个平方项，将其分开书写的结果）

对展开上式进⾏求导：

$\begin{aligned} \frac{\partial}{\partial w}[(Xw-y)^T(Xw-y)]=& \frac{\partial}{\partial w}[(w^TX^T-y^T)(Xw-y)] \\ \text{=}& \frac{\partial}{\partial w}(w^TX^TXw-w^TX^Ty-y^TXw+y^Ty) \\ \text{=}& X^TXw+X^TXw-X^Ty-X^Ty \end{aligned}$

需要求得求导函数的极⼩值，即上式求导结果为0，经过化解，得结果为：

$X^TXw=X^Ty$

经过化解为： $w=(X^TX)^{-1}X^Ty$

需要用到矩阵求导公式：

$\begin{gathered} \frac{dx^TA}{dx}=A \\ \frac{dAx}{dx}=A^T \\ \frac{\partial x^TAx}{\partial x}=(A+A^T)x \end{gathered}$

4、对数线性回归

$\ln y=\boldsymbol{w}^\mathrm{T}\boldsymbol{x}+b.$

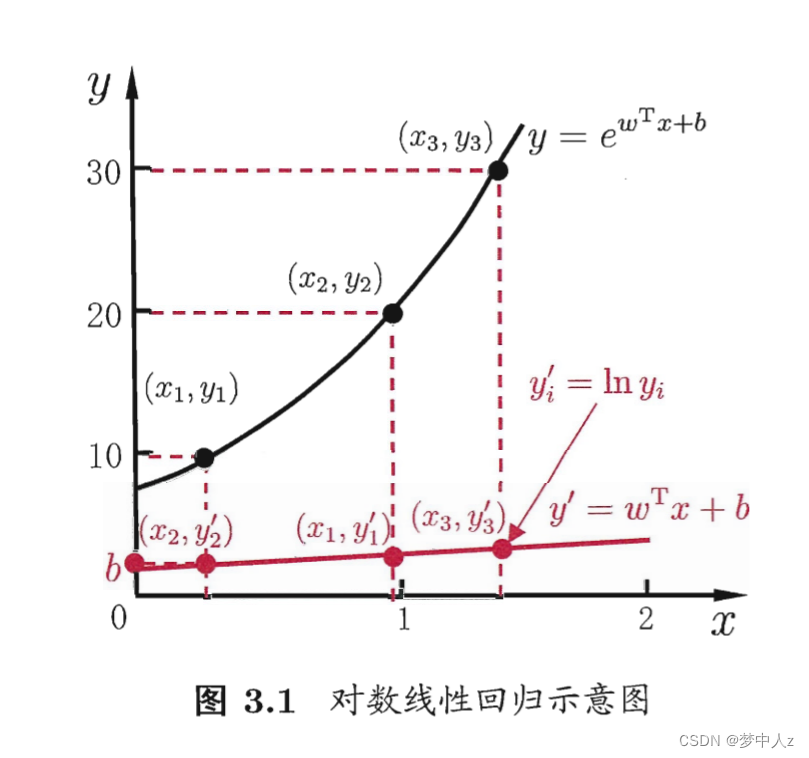
5、逻辑回归（对数几率回归）

注意：有文献译为 “逻辑回归”，但中文 “逻辑”与 logistic和 logit的含义相去甚远，因此西瓜书意译为 “对数几率回归”，简称 “对率回归”.

逻辑回归（Logistic回归，也称为Logit回归）被广泛用于估算一个实例属于某个特定类别的概率。用于分类问题居多。

逻辑回归模型也是计算输入特征的加权和（加上偏置项），但是不同于线性回归模型直接输出结果，它输出的是结果的数理逻辑值：

逻辑回归模型的估计概率： $\hat{p}=h_\theta(x)=\sigma(x^\mathrm{T}\theta)$

逻辑记为σ（·），是一个sigmoid函数（即S型函数），输出一个介于0和1之间的数字。

逻辑σ（·）即为下面定义：

对数几率函数： $y=\frac1{1+e^{-z}}.$

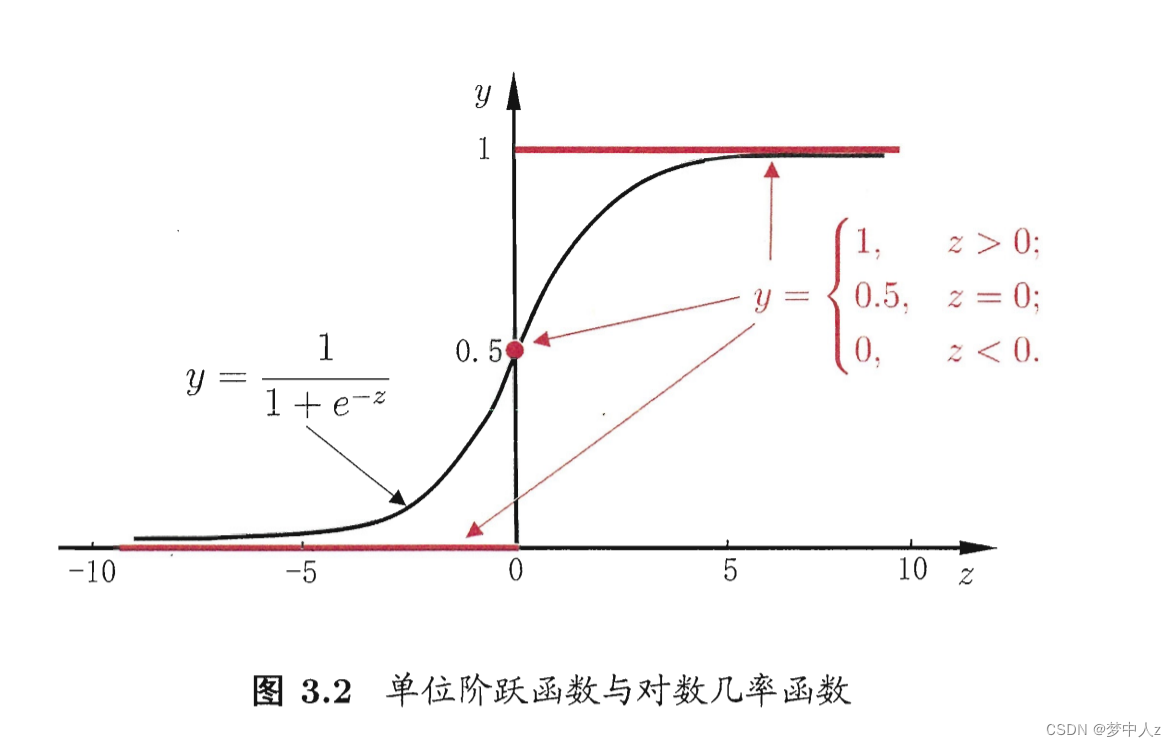
将对数几率函数作为 $g^{-}(\cdot)$ 得到：

$y=\frac1{1+e^{-(\boldsymbol{w}^\mathrm{T}\boldsymbol{x}+b)}}$

$\ln\frac y{1-y}=\boldsymbol{w}^\mathrm{T}\boldsymbol{x}+b\mathrm{~}$

由此可看出， $y=\frac1{1+e^{-(\boldsymbol{w}^\mathrm{T}\boldsymbol{x}+b)}}$ 实际上是在用线性回归模型的预测结果去逼近真实标记的对数几率，因此，其对应的模型称为“对数几率回归"。

其优点：

1、直接对分类可能性进行建模，无需事先假设数据分布，这样就避免了假设分布不准确所带来的问题；

2、它不是仅预测出“类别”，而是可得到近似概率预测，这对许多需利用概率辅助决策的任务很有用；

3、对率函数是任意阶可导的凸函数,有很好的数学性质，现有的许多数值优化算法都可直接用于求取最优解

逻辑回归模型预测

6、线性判别分析

LDA的思想非常朴素：给定训练样例集，设法将样例投影到一条直线上, 使得同类样例的投影点尽可能接近、异类样例的投影点尽可能远离；在对新样本进行分类时，将其投影到同样的这条直线上，再根据投影点的位置来确定新样本的类别。

6、多分类学习

二元分类器在两个类中区分，而多类分类器（也称为多项分类器）可以区分两个以上的类。

举个例子：将数字图片分为10类

“一对一”：为每一对数字训练一个二元分类器：一个用于区分0和1，一个区分0和2，一个区分1和2，以此类推。这称为一对一（OvO）

“一对多”：训练10个二元分类器，每个数字一个（0-检测器、1-检测器、2-检测器，以此类推）。然后，当你需要对一张图片进行检测分类时，获取每个分类器的决策分数，哪个分类器给分最高，就将其分为哪个类。这称为一对剩余（OvR）

参考文献：

GitHub - datawhalechina/pumpkin-book: 《机器学习》（西瓜书）公式详解

机器学习实战：基于Scikit-Learn、Keras和TensorFlow：原书第2版

线代，概率论等都有些忘记了，所以原理并未完全搞懂，之后复习好了回过头来看看

梦中人z

关注

18
点赞
踩
10

收藏

觉得还不错? 一键收藏
0
评论
学习吃瓜教程第3章线性模型总结

一对多”：训练10个二元分类器，每个数字一个（0-检测器、1-检测器、2-检测器，以此类推）。然后，当你需要对一张图片进行检测分类时，获取每个分类器的决策分数，哪个分类器给分最高，就将其分为哪个类。注意：有文献译为 “逻辑回归”，但中文 “逻辑”与 logistic和 logit的含义相去甚远，因此西瓜书意译为 “对数几率回归”，简称 “对率回归”.“一对一”：为每一对数字训练一个二元分类器：一个用于区分0和1，一个区分0和2，一个区分1和2，以此类推。,相应的，把数据集D 表示为一个。
复制链接

扫一扫

专栏目录