【算法训练（day4）】高精度与低精度计算模板

目录

一.整体思路

二.代码实现

---

一.整体思路

由于我们不能把一个非常大的数直接塞到int内部，我们需用把数据保存在string内部，这就导致我们需要手动模拟计算的相关过程。我们可以模拟竖式计算的过程来实现。（本文中的方法无法处理高精度与高精度的计算）

1.加法：

加法其实是比较简单的，我们首先从从低位算起，把较短的那个数按照每一位拆开，从最低位开始依次和较长的数字相加，将每一位的结果加起来就是最终结果，其实就是竖式相加的过程。如图，我们每次计算当前位和另一个数相加，结果的最低位就是当前位的值。（注意的是由于低位的计算会产生进位影响高位的值，我们需要一个进位t来保存下低位的进位并参与到高一位的计算中，也就是当前位计算结果去掉最低位就是进位）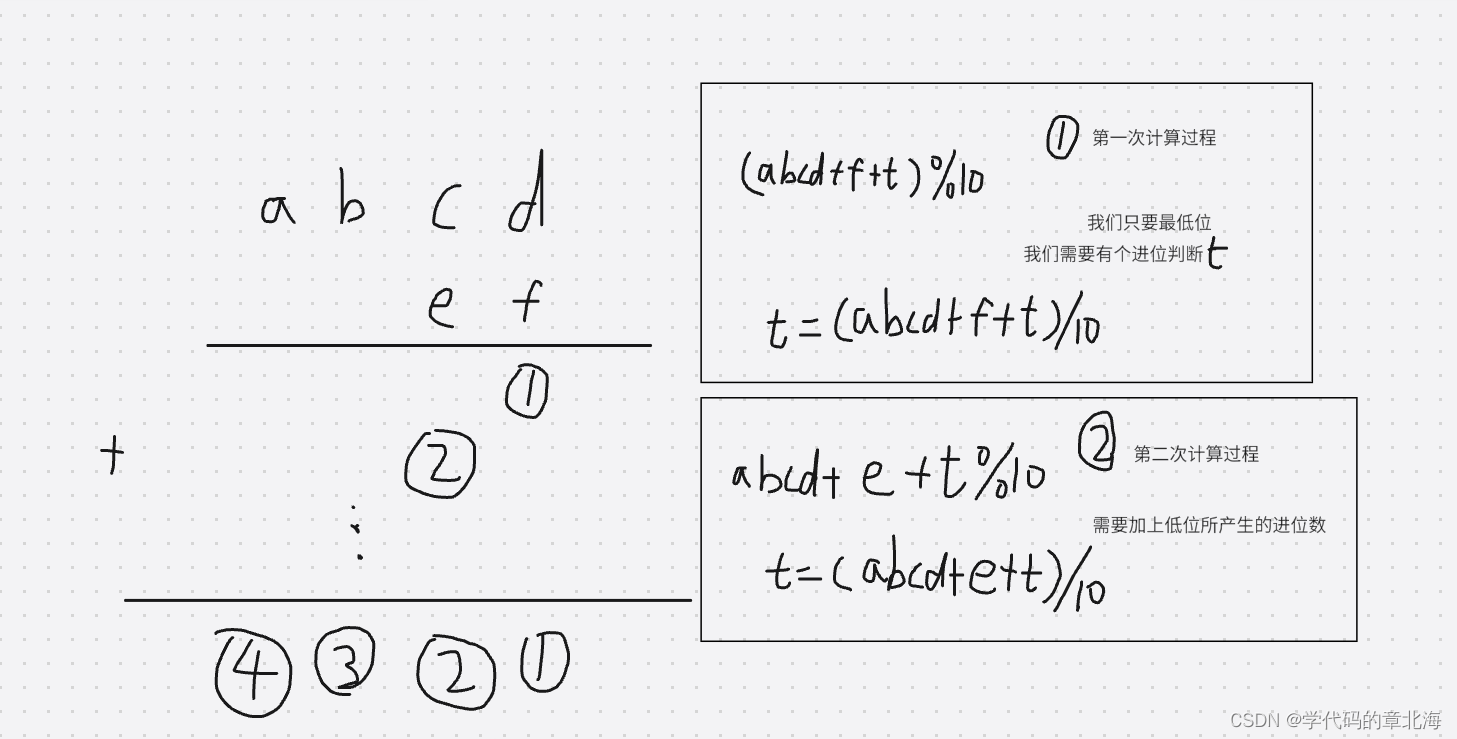

2.乘法思路 ：

乘法本质和加法是很相似的所以放在一起说：

乘法的竖式计算过程和加法是完全一致的，所以我们仍然可以从最低位算起每一位和另一个数相乘，取最低位作为当前位结果，并把前面的位作为进位t的新值。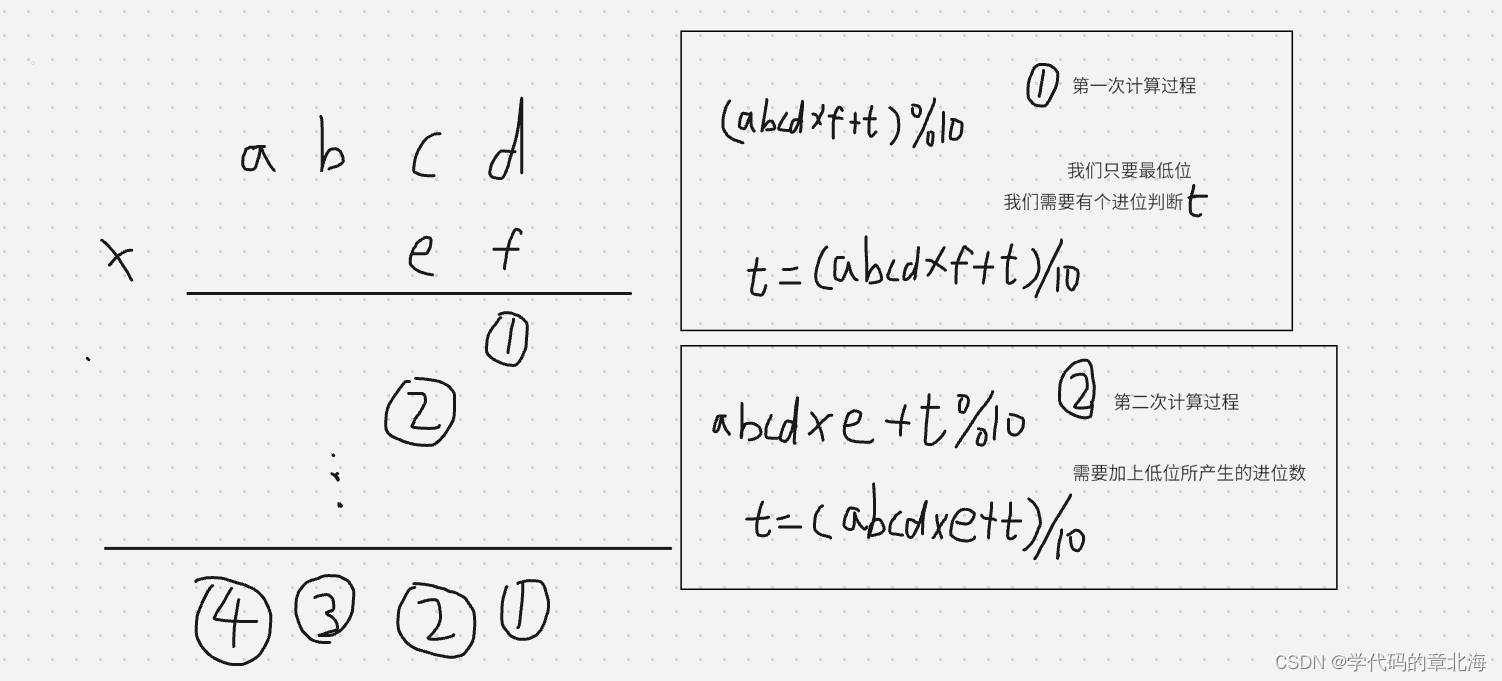

3.减法思路：

减法首先我们要让大的数作为被减数，小的数作为减数，通过标记位来判断正负，这样就能用同一段代码处理正数和负数的计算，同样也是从最低位到最高位以此相减，再遇到不够减的情况下，向下一位借10，同时让借位t变成1，证明借走了一位。在进行下一位的运算的时候，先让被减数减去上一位的借位之后再用同样的方法进行计算

4.除法思路：

触发有一点不一样，上面的三种方法都是从最低位开始计算，但除法是从最高位向低位进行计算。这点在竖式除法里也有体现，从最高位的每一位开始依次看够不够整除，不够的话就让当前位参与到下一位的计算。

二.代码实现

采用acwing里Y总的实现方式

1.加法

vector<int> add(vector<int> &A, vector<int> &B)
{
    if (A.size() < B.size()) return add(B, A);  //确保长的数字在上面

    vector<int> C;
    int t = 0;                                 //进位判断标志
    for (int i = 0; i < A.size(); i ++ )       //因为是倒叙输入，所以最开始取得就是最低位
    {
        t += A[i];                             // 先加上上一位的计算所产生的进位，
                                                //如果较短的数字当前位置有值在加上B的当前位
        if (i < B.size()) t += B[i];
        C.push_back(t % 10);                    //当前位置的计算结果就是上面相加后的最低位
        t /= 10;                                //最后把前面的其他位放在标记位里，参与下一轮计算
    }

    if (t) C.push_back(t);
    return C;
}

2.减法

vector<int> sub(vector<int> &A, vector<int> &B)
{
    vector<int> C;
    for (int i = 0, t = 0; i < A.size(); i ++ ) 
    {
        t = A[i] - t;                        //先判断是否因为上一次的计算产生借位问题，和加法不同的是，这里的借位只可能是1
        if (i < B.size()) t -= B[i];
        C.push_back((t + 10) % 10);    //同样只取末尾的位作为当前计算位的结果
        if (t < 0) t = 1;              //判断当前位的运算是否发生越界
        else t = 0;
    }

    while (C.size() > 1 && C.back() == 0) C.pop_back();  //去除前导0
    return C;
}

3.乘法

vector<int> add(vector<int>& A, int b)
{
	vector<int> c;
	int tmp = 0;
	for (size_t i = 0; i < A.size() || (tmp != 0); i++)  //计算叠加的过程在tmp上，在进位仍有值的时候仍要进行计算。
	{
		if (i < A.size())
		{
			tmp += A[i] * b;
		}
		c.push_back(tmp % 10);
		tmp = tmp / 10;       //剩余的高位进入标记位参与下一次计算
	}
	for (int i = c.size() - 1; c[i] == 0 && i > 0; i--)  //高位有可能会出现大量无意义的0需要去除掉
	{
		c.pop_back();
	}
	return c;
}

4.除法

vector<int> div(vector<int> check, int b, int& tmp)  //特殊点是只有除法是从最高位开始计算的所以所有的遍历数序是反的
{
    tmp = 0;
    vector<int> c;
    for (int i = check.size() - 1; i >= 0; i--)  //除法应该除以最高位未来保证模板一致，所以在传入vector的时候仍然倒序传入
    {
        tmp = tmp * 10 + check[i];  //当前值加上上一次余留的值
        c.push_back(tmp / b);
        tmp = tmp % b;
    }

    reverse(c.begin(), c.end());
    for (int i = c.size() - 1; c[i] == 0 && i > 0; i--)  //要先反转把高位的0反转到末尾，再用pop把末尾0清掉
    {
        c.pop_back();
    }
    return c;
}