关于一般直线的对称点_关于一条30度的直线对称的点-CSDN博客

本文链接：https://blog.csdn.net/m0_63018959/article/details/138158303

关于一般直线的对称点

结论

记点 $x_1,y_1)$ 关于直线 $A x + B y + C$ 的对称点为 $x_2,y_2)$ ，则
$\begin{cases} x_2=\frac{1}{A^2+B^2}[(B^2-A^2)x_1-2ABy_1-2AC] \\ y_2=\frac{1}{A^2+B^2}[(A^2-B^2)y_1-2ABx_1-2BC] \end{cases}$

推导过程

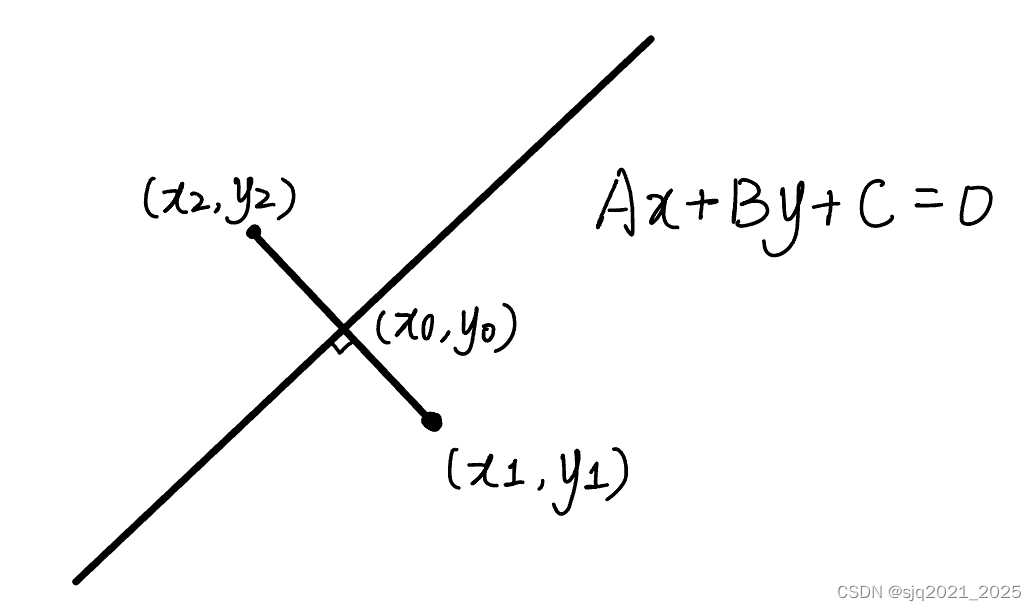
在这里插入图片描述

如图所示，考虑一般直线 $A x + B y + C = 0$ ，点 $x_1,y_1)$ 关于直线的对称点为 $x_2,y_2)$ ， $x_0,y_0)$ 为两对称点连线与直线的交点。根据对称点的性质有：
$\begin{aligned} &(x_2-x_0,y_2-y_0)=(x_0-x_1,y_0-y_1) \\ \Rightarrow \quad & \begin{cases} x_2=2x_0-x_1 \\ y_2=2y_0-y_1 \end{cases} \end{aligned}$
因为 $x_1,y_1)$ 已知，所以问题转换为求 $x_0,y_0)$ 。

根据对称点的性质，点 $x_0,y_0)$ 与点 $x_1,y_1)$ 构成的向量与直线垂直，即向量积为0。因此
$(x_0-x_1,y_0-y_1)\cdot(B,-A)=0 \quad \Rightarrow \quad B(x_0-x_1)=A(y_0-y_1)$
又因为点 $x_0,y_0)$ 在直线上，所以
$Ax_0+By_0+C=0$
解方程组
$\begin{cases} B(x_0-x_1)=A(y_0-y_1)\\ Ax_0+By_0+C=0 \end{cases}$
得：
$\begin{cases} x_0=\frac{1}{A^2+B^2}(B^2x_1-ABy_1-AC) \\ y_0=\frac{1}{A^2+B^2}(A^2y_1-ABx_1-BC) \end{cases}$
进而：
$\begin{cases} x_2=\frac{1}{A^2+B^2}[(B^2-A^2)x_1-2ABy_1-2AC] \\ y_2=\frac{1}{A^2+B^2}[(A^2-B^2)y_1-2ABx_1-2BC] \end{cases}$