C++之STL

最新推荐文章于 2024-11-12 13:55:23 发布

m0_63098318

最新推荐文章于 2024-11-12 13:55:23 发布

阅读量981

点赞数 36

文章标签： c++ 算法开发语言

本文链接：https://blog.csdn.net/m0_63098318/article/details/142871130

版权

STL标准库

#include <string>      //字符串
#include <vector>      //动态数组 在尾部高效地插入和删除元素，但在中间和头部进行插入和删除操作时效率较低。
                       //它支持随机访问迭代器，底层结构为动态数组。
                       //在需要随机访问且频繁在尾部进行操作的场景中特别有用。
#include <list>        //双向链表  可在任意位置高效地插入和删除元素，但不能随机访问 
#include <queue>       //队列 常用于广度优先搜索

#include <unordered_map> //无序映射(键值对) 也叫哈希表 具有更快的查找和插入速度
#include <unordered_set> //无序集合  不支持有序遍历但查找和插入速度非常快
#include <map>         //有序映射
#include <set>       //有序集合  用于快速检索、去重和排序操作
#include <stack>     //栈 后入先出
#include <multiset>   //multiset允许元素重复的set版本，其他特性与set相同
#include <multimap>   //multimap允许键重复的map版本，支持多个相同键的键值对

字符串string

构造/创建

//定义
string s1();   //s1为空
string s2("hello");
string s3(4,'w');    //s3="wwww";
string s4("12345",1,3);   //s4="234";
string s5 = { 'a','c','3'};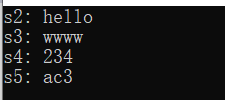

遍历/访问

// 遍历/访问
//采用[]下标访问
int main ()
{
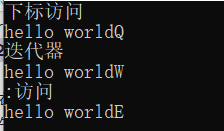
    string s("hello worldQ");
    for (size_t i = 0; i < s.size(); i++)
    {
        cout << s[i];
    }
    cout << endl;
    return 0;
}
//采用迭代器(地址)访问
int main ()
{
    string s("hello worldW");
    string::iterator it = s.begin();
    while (it != s.end())
    {
        cout << *it;
        ++it;
    }
    cout << endl;
    return 0;
}
//for遍历
int main ()
{
    string s("hello worldE");
    for (auto ch : s)
    {
        cout << ch;
    }
    cout << endl;
    return 0;
}

//find正向查  rfind反向查
int main()
{
    string v1("hello worldQ");

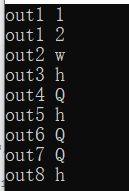
    auto out1=v1.find('e', 1); //在s中从索引1开始查找e的位置 默认从0开始
    cout << "out1 " << out1 << endl;
    out1 = v1.find("ll"); //在s中从in开始查找str的位置 in默认为0
    cout << "out1 " << out1 << endl;

    //按索引访问 不能超出边界
    auto out2=v1.at(6);//返回v1的第6个元素
    cout << "out2 " << out2<<endl;

    auto out3 = v1.front();//返回第一个元素
    cout << "out3 " << out3 << endl;

    auto out4 = v1.back();//返回最后一个元素
    cout << "out4 " << out4 << endl;

    //迭代器 我理解为指针
    auto out5 = v1.begin();//返回一个迭代器,指向第一个元素
    cout << "out5 " << *out5 << endl;

    auto out6 = v1.end();//返回迭代器,指向最后一个元素的下一位 为空
    cout << "out6 " << *(out6-1) << endl;

    auto out7 = v1.rbegin();//反向迭代器,指向最后一个元素
    cout << "out7 " << *out7 << endl;

    auto out8 = v1.rend();//反向迭代器,指向第一个元素之前的位置,访问第一个需要-1
    cout << "out8 " <<  *(out8 - 1) << endl;

    return 0;
}

增加

//插入
//单插字符
int main()
{
    string s("hello ");
    s.push_back('w');// 插入常量字符串
    s.push_back('s');// 插入另一个字符
    for (size_t i = 0; i < s.size(); i++)
    {
        cout << s[i];
    }
    return 0;
}
//尾插字符串
int main()
{
    string s("hello ");
    s.append("world");// 插入常量字符串
    string str("world");
    s.append(str);// 插入另一个string对象
    return 0;
}
//+=运算 常用
int main()
{
    string s("hello ");
    s += "world"; // 插入常量字符串
    string str("world");
    s += str; // 插入新的string对象
    s += 'A';// 插入单个字符

    return 0;
}
//insert
int main()
{
    string s("hello");

    // 在下标为0的位置插入一个新的string对象
    string str("hello world");
    s.insert(0, str);
    // 在下标为0的位置插入一个常量字符串的前3个字符
    s.insert(0, "hello world", 3);

    // 在下标为0的位置插入一个字符x
    s.insert(0, 1, 'x');
    s.insert(s.begin(), 'x');
    // 在下标为0的位置插入三个字符x
    s.insert(0, 3, 'x');

    return 0;
}

删除

//erase函数
int main ()
{
    string s("hello world");
    // 删除下标为3位置的一个字符
    s.erase(3, 1);
    s.erase(s.begin()+3);
    // 删除以下标为3位置为起点的3个字符
    s.erase(3, 3);
    s.erase(s.begin() + 3, s.begin() + 6);
    // 删除以下标为3位置为起点往后的所有字符
    s.erase(3);
    
    return 0;
}
//pop_back 尾删单个字符
int main ()
{
    string s("hello world");
    s.pop_back();
    cout << s << endl;
    return 0;
}

其他

//求长度
int main ()
{
    string s("hello world");
    cout << s.size() << endl;//容器目前存在的元素数
    cout << s.capacity() << endl;//容器能存储数据的个数
    return 0;
}
//capacity 一般大于size的原因是为了避免每次增加数据时都要重新分配内存，
//所以一般会生成一个较大的空间，以便随后的数据插入。
//reserve()     指定容器能存储数据的个数
//resize()     重新指定有效元素的个数，区别与reserve()指定容量的大小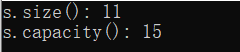

//两个字符串交换 .swap()
int main ()
{
    string s1("hello world");
    string s2("string");
    s1.swap(s2);

    cout << s1 << endl;
    cout << s2 << endl;
    return 0;
}

//截取  .substr()
int main()
{
    string s1("hello world");
    // 取出子串"world"
    string s2 = s1.substr(6, 5);//从索引6开始截取5个字符
    cout << s2 << endl;
    return 0;
}

//流提取 键盘输入 
//常规cin输入时 遇到空格会停止；getline函数可以获取一行字符串，遇到换行符停止
int main()
{
    // 键盘输入字符串"hello world"
    string s;
    // cin s; // 这种写法遇到空格会停止
    getline(cin, s);
    cout << s << endl;
    return 0;
}

数组vector

构造/创建

int main()
{
    vector<int> vec1; //空的整形vector，没有给他添加任何元素。
    vector<float> vec2(3);//始化了一个有3个元素的vector，由于并没有指定初始值，将会使用编译器默认的初始值
    vector<char> vec3(3,'a'); //有3个a的字符vector，括号中第二个值代表着所有元素的指定值。
    vector<char> vec4(vec3); //通过拷贝vec3中的元素初始化vec4，它们的元素会一模一样。
    return 0 ;
}

遍历/访问(同string)

增加

//尾插push_back
v1.push_back(9);//向向量尾部增加一个元素整数9

//insert 在指定位置插入
iterator it =v1.begin()+3;//定义it迭代器,it指向v1第4个元素
v1.insert(it,9);//在迭代器it前增加1个数9

iterator it =v1.begin()+3;//定义it迭代器,it指向v1第4个元素
v1.insert(it,2,9);//在迭代器it前增加2个数9

iterator it =v1.begin()+3;//定义it迭代器,it指向v1第4个元素
v1.insert(it,2,v2.begin(),v2.end());//在迭代器it前增加v2整个数据

删除

// erase 通过地址删除
iterator it=v1.begin()+3;//定义it迭代器,it指向v1第4个元素
v1.erase(it+1);//删除it后面的元素

iterator it=v1.begin();//定义it迭代器,it指向v1第1个元素
v1.erase(it,it+3);//删除v1前3个元素

//pop_back()尾删
v1.pop_back();//删除v1最后一个元素

//清空
v1.clear();//清除向量中所有元素

其他

// resize() 指定有效元素   reserve()空间可以存放
int main()
{
    vector<char> v1(3, 'a');
    cout << "v1.size(); " << v1.size() << endl;
    cout << "s.capacity(): " << v1.capacity() << endl;
    v1.reserve(20); //reserve()     指定容器能存储数据的个数
    cout << "v1.size(); " << v1.size() << endl;
    cout << "s.capacity(): " << v1.capacity() << endl;
    v1.resize(2); //resize()     重新指定有效元素的个数，区别与reserve()指定容量的大小
    cout << "v1.size(); " << v1.size() << endl;
    cout << "s.capacity(): " << v1.capacity() << endl;
    return 0;
}
//capacity 一般大于size的原因是为了避免每次增加数据时都要重新分配内存，
//所以一般会生成一个较大的空间，以便随后的数据插入。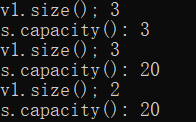

//判断是否为空
v1.empty();

v1.size();//返回向量中元素个数

v1.capacity();//返回当前向量容量 

v1.max_size();//返回最大允许vector数量

v1.swap(v2);//交换v1和v2的数据

v1.assign(9,5);//设置前5个元素值为9

v1.assign(it,v1.begin()+1,v1.end()-1);//从指定开始到指定结尾设置为it指向的元素

链表list(STl库实现)

链表的定义/链表是什么？

顺序表(如vector)将元素存放在连续的空间上，每个地址存放一个存储单元(元素)，在进行增删时需要挪动大量元素。而单链表的元素存放空间是不连续的，在每一个地址的存储单元有两个元素：当前地址的值与下一个位置的地址，在增删时只需要更改指定位置前后的指针，同时这也导致了无法随意存取。

在链表中也称一个地址为一个节点。

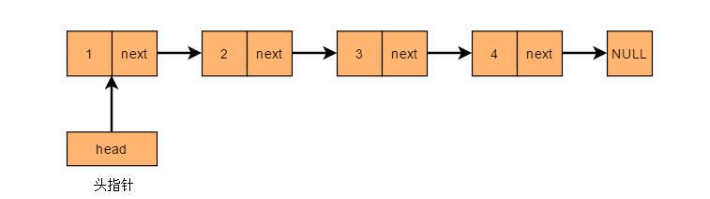
实现上分类：

动态链表、静态链表、STL list。具体见下面链接

【一】一起算法---链表：动态链表、静态链表、STL list_动态链表静态链表st l列表-CSDN博客

list容器使用双链表实现；双链表将每个元素存储在不同的位置，每个节点通过next，prev指针链接成顺序表。

优点：允许在序列中的任何位置执行固定O(1)时间复杂度的插入和删除操作，并在两个方向进行迭代。

缺点：list和forward_list（单链表实现）不能通过位置直接访问元素；例如，要访问列表中的第五个元素，必须从已知位置（开始或结束）迭代到该位置，需要哦线性时间开销。

构造函数/初始化

int main()
{
    list<int> list1 = { 12,23,34 };
    list<int> list2(3, 11);  //构造拥有 3 个有值 11 的元素的容器链表。
    list<int> list3(list2);  //拷贝list2

    list<string> list4 = { "This","is","windows" }; //默认
    list<string> list5;  //空列表
    list<string> list6;

    list5 = list4;  //拷贝

    list6.assign(3, "This");//以 3 份 "This" 的副本替换内容
}

遍历/访问

STL list的访问是通过迭代器实现的，迭代器与指针在vector访问元素时，区别不太大 *迭代器就可以访问元素。但是在list中，按照概念来说，每一个节点包含一个val成员和两个指针成员(前后)，如果知道该节点的地址，那么访问指针成员就可以知道下一个或上一个节点的地址，按照道理来说 (*指针).right可以访问下一个节点的地址，但是迭代器不提供这个功能。 *迭代器得到的是val值，而迭代器++是下一节点的迭代器，想要访问地址只能 &(*迭代器) ，这个地址是val值的地址。

// 访问
int main()
{
    list<int> list1 = { 12,23,34 };

    cout << "list1.front()：" << list1.front() << endl;  //头
    cout << "list1.back()：" << list1.back() << endl;  //尾
    
    return 0;
}

//遍历
//.begin() .rbegin() .end() .rend()对list适用

int main()
{
    list<int> list1 = { 12,23,34 };

    list<int>::const_iterator it1 = list1.begin();
    for (; it1 != list1.end(); it1++)
    {
        cout << *it1 << "\t";
    }

    cout << endl;

    list<int>::reverse_iterator it2 = list1.rbegin() ;
    for (; it2 != list1.rend(); it2++)
    {
        cout << *it2 << "\t";
    }

    cout << endl;
    
    return 0;
}

增加


int main()
{
    list<int> list1 = { 12,23,34 };
    list<int> list2 = { 1,2,3,4,5 };

    Lst1.push_back() ;//在list的末尾添加一个元素 ；
    Lst1.push_front() ;//在list的头部添加一个元素

    auto it = list1.begin();// it为list的首个元素的地址
    list1.insert(it, 55);//在it前添加一个55 it指向12的地址

    it++;
    list1.insert(it, 3, 55);//在it前添加3个55  it指向23的地址

    list1.swap(list2);//1和2交换


    return 0;
}

删除

lst1.erase(it);  //删除it处的值
Lst1.clear(); // 删除所有元素
Lst1.erase(); // 删除一个元素
Lst1.unique();// 删除list中重复的元素
Lst1.pop_back(); // 删除最后一个元素 ；
Lst1.pop_front(); // 删除第一个元素

修改

int main()
{
    list<int> list1 = { 12,23,34 };
    list<int> list2 = { 1,2,3,4,5 };
    
    list1.resize(); //改变list的大小
    list1.reverse(); // 把list的元素倒转


    return 0;
}

查

Lst1.front(); // 返回第一个元素 ；
Lst1.back(); //返回最后一个元素
Lst1.empty(); // 如果list是空的则返回true
Lst1.max_size(); // 返回list能容纳的最大元素数量 ；
Lst1.size(); // 返回list中的元素个数

其他

int main()
{
    list<int> list1 = { 12,23,34 };

    cout << "list1.empty():" << list1.empty() << endl; //判断是否为空
    cout << "list1.size():" << list1.size() << endl;  //判断长度
    cout << "list1.max_size():" << list1.max_size() << endl;  //容量

    return 0;
}

队列queue

构造/创建

//只能创建空的 不能初始化赋值
//默认为双向队列
queue<int>q1; //定义一个储存数据类型为int的queue容器q1 
queue<double>q2; //定义一个储存数据类型为double的queue容器q2
queue<string>q3; //定义一个储存数据类型为string的queue容器q3
queue<结构体类型>q4; //定义一个储存数据类型为结构体类型的queue容器q4

增加/弹出/删除

.empty() //判断队列是否为空 
.size() //返回队列中元素的个数
//弹处(不会在队列中删除元素本身) 
.front() //返回队列中的第一个元素 
.back() //返回队列中最后一个元素 
//删
.pop() //删除队列的第一个元素 
//添加
.push() //在队列末尾加入一个元素

遍历

//输出队头并删除队头
int main()
{
    queue<int> q; //定义一个数据类型为int的queue
    q.push(1); //向队列中加入元素1 
    q.push(2); //向队列中加入元素2
    q.push(3); //向队列中加入元素3
    q.push(4); //向队列中加入元素4
    while(!q.empty())
    {
        cout<<q.front()<<" ";
        q.pop();
    }    
}

栈stack

构造/创建

//只能创建空的 不能初始化赋值
stack<int> mystack; //定义一个储存数据类型为int的mystack容器mystack
stack<double>s2; //定义一个储存数据类型为double的mystack容器s2
stack<string>s3; //定义一个储存数据类型为string的mystack容器s3
stack<结构体类型>s4; //定义一个储存数据类型为结构体类型的queue容器s4

增加/弹出/删除

.empty() //判断队列是否为空 
.size() //返回队列中元素的个数
//弹处(不会在队列中删除元素本身) 
.top() //返回栈顶元素 
//删
.pop() //删除栈顶元素 
//添加
.push() //在栈末尾加入一个元素

遍历

//输出队头并删除队头
int main()
{
    stack<int> s; //定义一个数据类型为int的queue
    s.push(1); //向队列中加入元素1 
    s.push(2); //向队列中加入元素2
    s.push(3); //向队列中加入元素3
    s.push(4); //向队列中加入元素4
    while(!q.empty())
    {
        cout<<q.top()<<" ";
        s.pop();
    }    
}

组/对 pair

pair是将2个数据组合成一组数据，pair的底层实现是一个结构体，主要的两个成员变量是first与second，因为是struct而不是class，所以可以直接使用pair的成员变量。

构造/创建

pair<T1, T2> p1;            //创建一个空的pair对象（使用默认构造），它的两个元素分别是T1和T2类型，采用值初始化。
pair<T1, T2> p1(v1, v2);    //创建一个pair对象，它的两个元素分别是T1和T2类型，其中first成员初始化为v1，second成员初始化为v2。
make_pair(v1, v2);          // 以v1和v2的值创建一个新的pair对象，其元素类型分别是v1和v2的类型。

其他

p1 < p2;                    // 两个pair对象间的小于运算，其定义遵循字典次序：如 p1.first < p2.first 或者 !(p2.first < p1.first) && (p1.second < p2.second) 则返回true。
p1 == p2；                  // 如果两个对象的first和second依次相等，则这两个对象相等；该运算使用元素的==操作符。
p1.first;                   // 返回对象p1中名为first的成员变量
p1.second;                 // 返回对象p1中名为second的成员变量

映射/哈希表unordered_map

unordered_map内部是一个个pair，在map一般称pair的first称为键key，second称为值value，map也可叫做键值对。unordered_map在存储pair时是没有顺序的，会根据键key的值锁定所在的pair进而查找到值value。

构造/创建

int main()
{
    // 默认构造函数：空 unordered_map
    unordered_map<int, string> m1;

    // 列表构造函数  键重复出现时，值保存为第一次出现的值
    unordered_map<int, string> m2 = { {1,"This"},{2,"is"}，{3,"Th"},{2,"an"} };

    // 复制构造函数
    unordered_map<int, string> m3 = m2;

    // 移动构造函数
    unordered_map<int, string> m4 = move(m3);

    // 范围构造函数
    unordered_map<int, string> m5(m3.begin(), m3.end());

    return 0;
}

遍历

//迭代器
int main()
{ 
    unordered_map<int, string> m1 = { {1,"This"},{2,"is"},{3,"an"},{4,"apple"} };
    
    for (auto it = m1.begin(); it != m1.end(); it++)
    {
        cout << it->first <<"  " <<it->second << endl;
    }

    return 0;
}

增加

int main()
{    
    unordered_map<int, string> m1 = { {1,"This"},{2,"is"},{3,"an"},{4,"apple"} };
    m1.insert({ 5,"three" });//三种添加方式都是存在键时不操作，不存在键添加
    m1.emplace(6, "u盘");    
    m1.try_emplace(7, "uuu盘"); 
    //三种方法在操作上有区别
    //inset 先创建临时对象
    //emplace  在map存储上创建 如果存在就不放入到map里
    //try_emplace 在map空间创建 在不存在时与emolace相同 存在不进行操作

    m1.insert_or_assign(7, "windows"); //如若在6这个键 则将值改为windows，否则添加这个键值对
    m1.clear() ;//清空
    
    return 0;
}

删除

map<int, string> myMap;
myMap[1] = "one";
myMap[2] = "two";
myMap[3] = "three";
myMap[4] = "four";
myMap.erase(1); // 删除键为1的键值对
myMap.erase(m1.begin()); // 删除迭代器it指向的键值对

map<int, string>::iterator it1 = myMap.find(1);
map<int, string>::iterator it2 = myMap.find(3);
myMap.erase(it1, it2); // 删除从it1到it2之间的所有键值对

改

m1.swap(m2); //两个互换

查

int main()
{

    unordered_map<int, string> m1 = { {1,"This"},{2,"is"},{4,"an"},{3,"apple"},{1,"summer"} };

    string x = m1.at(4);//返回键为4的值
    cout << "m1.at(1): " << x << endl;

    auto it = m1.find(2);//返回键为2的指针 通过->访问pair的键值
    cout << it->first << "-->" << it->second << endl;

    auto range = m1.equal_range(1);
    for (auto it = range.first; it != range.second; ++it) 
    {
        std::cout << it->first << "--->" << it->second << '\n';
    }
//返回的是迭代器类型的pair
//pair<map<int, int>::iterator,map<int, int>::iterator>range
//其中键位想要找的的那个键所在的迭代器  值位所在迭代器的下一位
    return 0;
}

其他

int main()
{    
    unordered_map<int, string> m1 = { {1,"This"},{2,"is"},{3,"an"},{4,"apple"} };
    
    cout << "m1.empty():" << m1.empty() << endl; //检查容器是否无元素
    cout << "m1.size():" << m1.size() << endl; //返回容器中的pair数
    cout << "m1.max_size():" << m1.max_size() << endl;//最大容量


    
    return 0;
}

无序集合unordered_set

unordered_set与unordered_map大体类似，map内元素含有键与值，单set仅包含键，在成员函数(增删查改)用法上没有区别。

有序映射mat/有序集合set

mat与unordered_map、set与unordered_set的区别仅在于元素的存储上，map与set都是有序的，按照键的升序进行排列，而unordered_set与unordered_map是按照添加元素的顺序进行排列。

重复的map/set multimap/multiset

map与muitimap大体上相同，唯一不同就是，map中key是唯一的，multimap中key是可以重复的。set同理

结构体

链表(单向)(动态链表)

动态链表在程序运行时通过指针动态地创建和删除节点，从而灵活调整链表的大小。这种方法使得内存管理变得复杂，但同时也提供了高度的灵活性和效率。在实现过程中，每个节点都是在需要时通过内存申请函数（如C语言中的malloc或C++中的new）动态分配的。(讯飞星火大模型给出)

链表的定义与STL list相同

单链表的结构体表示

//该方法缺点为构造时必须独立定义节点 无法像STL标准库中容器一样初始化时定义多个节点
struct ListNode {
    int val;
    ListNode* next;
    ListNode() : val(0), next(nullptr) {}
    ListNode(int x) : val(x), next(nullptr) {}
    ListNode(int x, ListNode* next) : val(x), next(next) {}
};
//根据传参的不同，定义三种类型
// 1.无参： 值为0，下一个元素地址为空NULL
// 2.只有元素参数： 值为指定参数，下一个元素地址为空NULL
// 3.元素+地址：值为指定参数，下一个元素地址为指定地址

//后续创建的节点均采用这一结构体

初始化/创建

在创建方面，STL list通过push_back()、push_front()能够在链表首尾添加节点值，自动创建节点和指针指向。而结构体的实现方式中，需要通过new手动创建一个链表节点，并且找到想要插入的位置(首、尾、中间)前后的节点手动修改指向才能让节点与链表连接起来。

int main()
{
    //利用指针创建  new出来的都是指针类型 因此前面含有*
    ListNode* head = new Node();//利用结构体进行创建， 地址存放元素为默认值
    cout << head->data << endl;
    ListNode* head1 = new Node1(10);//利用结构体进行创建， 地址存放元素为10    
    cout << head1->data << endl;
    
    //利用定义创建
    ListNode head2; //定义一个结构体对象
    p.val = 1;  //将结构体对象的成员赋值
    p.next = NULL; //将结构体对象的成员赋值 如果不赋值默认NULL 
    return 0;
}
//力扣中给的函数体形参都是第一种 形参为结构体地址

链表节点链接

int main()
{
    //利用指针创建 因为创建的是地址/指针 所以访问地址上成员内容时使用->
    ListNode* head = new ListNode();//利用new进行创建， 地址存放元素为默认值
    cout << head->val << endl;
    ListNode* head1 = new ListNode(10);//利用new进行创建， 地址存放元素为10    
    cout << head1->val << endl;
    
    //链接
    head->next = head1;//head的指针指向head1 
    auto out = head->next->val; //head的下一个节点的元素 
    cout << "out: " <<out<< endl; // 输出 out: 10
    
    //利用定义创建 定义结构体时访问成员内容使用.
    ListNode head2; //定义一个结构体对象
    head2.val = 1;  //将结构体对象的成员赋值
    head2.next = NULL; //将结构体对象的成员赋值 如果不赋值默认NULL 
    ListNode head3; //定义一个结构体对象
    head3.val = 9;  //将结构体对象的成员赋值

    head2.next = &head3;
    out = head2.next->val; //head2的下一个节点的元素
    cout << "out: " << out << endl; // 输出 out: 9
   
    //创建时链接
    ListNode* head4 = new ListNode(5); //创建首节点
    head4->next = new ListNode(6);//创建首节点的下一个节点
    head4->next->next = new ListNode(7);//创建首节点的下下个节点
    //通过此种方法创建的链表只知道首节点 想要访问其余节点需要进行遍历

    return 0;
}

遍历

因为链表自身的特性(链表的元素存放空间是不连续的)，因此无法使用像顺序容器(string、vector)索引及首地址++的方式进行遍历，想要遍历采用结构体成员next进行遍历。

int main()
{
    //创建了含有7个节点的单链表
    ListNode* head = new ListNode(7);
    head->next = new ListNode(6);
    head->next->next = new ListNode(5);
    head->next->next->next = new ListNode(4);
    head->next->next->next->next = new ListNode(3);
    head->next->next->next->next->next = new ListNode(2);
    head->next->next->next->next->next->next = new ListNode(1);
//遍历的核心是迭代/循环 for或者while都可以
//1.根据当前地址输出成员val
//2.根据当前地址成员next更新当前地址
//3.当更新后地址为空(为空意味着输出了链表最后一个节点 此时地址尾表尾/指针指向了表尾)时停止循环
//下列while或者for二选一
    while (head!= NULL)
    {
        cout << head->val <<" ";
       head= head->next;
    }
    cout << endl;
    for(auto i=head; head!=NULL; head=head->next)
    {
        cout << head->val << " ";
    }
//注意的是遍历结束后 head指向了链表尾 head->val输出表尾的val此代码中为1，
//如果扔想指向表头 需要在遍历前备份一个指针 
//ListNode* h = head；cout << h->val << endl;输出为7
    return 0;
}

增/插入节点

//增加或插入节点
//头插
int main()
{
    //创建
    ListNode* head = new ListNode(7);
    head->next = new ListNode(6);
    head->next->next = new ListNode(5);
    ListNode* head1 = new ListNode(8);
    head1->next = head;//此时表头变为8所在的地址 head1是8的地址 head是7的地址
    head = head1;//此时将head的内容由7的地址变为8的地址 首地址的字母还是head 但存放的地址变为了8的地址
    //最后一步 head = head1;仅仅是为了符号同意 head一直表示表头
    while (head != NULL)
    {
        cout << head->val << " ";
        head = head->next;
    }// 输出： 8 7 6 5
    return 0;
}
//尾插 采取遍历的方法
int main()
{
    //创建
    ListNode* head = new ListNode(7);
    head->next = new ListNode(6);
    head->next->next = new ListNode(5);
    ListNode* head1 = new ListNode(8);

    ListNode* h = head;//表头备份 防止遍历后head指向表尾
    //遍历链表 得到表尾
    while (head->next!=NULL) 
    {
        head = head->next;
    }
    head->next= head1;//让表尾的指针指向要插入的 即当前表尾成员的next为head1的地址 
    head = h; //head存放的地址改为备份的表头
    while (head != NULL)
    {
        cout << head->val << " ";
        head = head->next;
    }//输出： 7 6 5 8
    return 0;
}
//任意插
int main()
{
    int i = 2,id=1; //i为要插入位置“索引”
    //创建
    ListNode* head = new ListNode(7);
    head->next = new ListNode(6);
    head->next->next = new ListNode(5);
    head->next->next->next = new ListNode(4);
    head->next->next->next->next = new ListNode(3);

    ListNode* head1 = new ListNode(9);//要插入的节点

    ListNode* h = head;//表头备份 防止遍历后head指向表尾
    
    //遍历链表 得到要插入位置前一个节点  
    while (i!=id)
    {
        head = head->next;
        id++;
    }

    head1->next = head->next;//将要插的入的节点的next指向原索引节点
    head->next = head1;
 
    head = h; //head存放的地址改为备份的表头
    while (head != NULL)
    {
        cout << head->val << " ";
        head = head->next;
    }//输出： 7 6 9 4 3
    return 0;
}

插入链表

//增加或插入链表 表1 表2两个链表
//head2插入head1后  head1插入head2后同理  
int main()
{
    //创建
    //表1
    ListNode* head1 = new ListNode(7);
    head1->next = new ListNode(6);
    head1->next->next = new ListNode(5);
    head1->next->next->next = new ListNode(4);
    head1->next->next->next->next = new ListNode(3);
    //表2
    ListNode* head2 = new ListNode(11);
    head2->next = new ListNode(12);
    head2->next->next = new ListNode(13);
    head2->next->next->next = new ListNode(14);
    head2->next->next->next->next = new ListNode(15);
    
    //复制表1的头
    ListNode* head = head1;
 
    //当head1节点下一个是空意味着此时head1已经是表1的尾
    while (head1->next != NULL)
    {

        head1 = head1->next;
    }
    //表1的尾下一个是表2的头
    head1->next = head2;


    while (head != NULL)
    {
        cout << head->val << " ";
        head = head->next;
    }//输出： 7 6 5 4 3 11 12 13 14 15
    return 0;
}

//head2整体插入在heda1内
int main()
{
    //创建
    //表1
    ListNode* head1 = new ListNode(7);
    head1->next = new ListNode(6);
    head1->next->next = new ListNode(5);
    head1->next->next->next = new ListNode(4);
    head1->next->next->next->next = new ListNode(3);
    //表2
    ListNode* head2 = new ListNode(11);
    head2->next = new ListNode(12);
    head2->next->next = new ListNode(13);
    head2->next->next->next = new ListNode(14);
    head2->next->next->next->next = new ListNode(15);
    //head2插入head1后
    
    //复制表1的头
    ListNode* head = head1;
    //复制表2的头
    ListNode* head2_2 = head2;
 
    //当head2节点下一个是空意味着此时head2已经是表1的尾
    while (head2->next != NULL)
    {
        head2 = head2->next;
    }
    //此时 head heda1 均为表1的头 head2为表2的尾 head2_2为表2的头 下一步将head1变为插入节点前一个节点


    int i = 3, id = 1;//i尾要插入的节点

    while (i != id)
    {
        head1 = head1->next;
        id++;
    }

    //此时head1尾插入节点前一个节点  
    head2->next = head1->next;//表2节点指向插入节点
    head1->next = head2_2;//插入节点前节点指向表2头

    while (head != NULL)
    {
        cout << head->val << " ";
        head = head->next;
    }//输出： 7 6 5 11 12 13 14 15 4 3
    return 0;
}

删除节点

//删除头节点 最简单
head=head->next;

//删除尾节点
//链表只有一个节点
head=head->next;/*或者*/head=NULL;
///链表两个节点
head->next=NULL;
//链表含有两个及以上节点
int main()
{
    //创建
    ListNode* head = new ListNode(7);
    head->next = new ListNode(6);
    head->next->next = new ListNode(5);

    ListNode* h = head;//表头备份 防止遍历后head指向表尾
    //遍历链表 得到表尾前一个  head->next为表尾 表尾的下一个为空
    while (head->next->next!=NULL) 
    {
        head = head->next;
    }
    head->next= NULL;//让表尾为空  
    head = h; //head存放的地址改为备份的表头
    while (head != NULL)
    {
        cout << head->val << " ";
        head = head->next;
    }//输出： 7 6 
    return 0;
}

//中间删除 主要求得删除位置前一个地址 让该地址的成员next指向删除位置的下一个 
//即 删的前一个位置->next=删的前一个位置->next->next;
int main()
{
    int i = 2,id=1; //i为要删除位置“索引” id为初始值
    //创建
    ListNode* head = new ListNode(7);
    head->next = new ListNode(6);
    head->next->next = new ListNode(5);
    head->next->next->next = new ListNode(4);
    head->next->next->next->next = new ListNode(3);

    ListNode* h = head;//表头备份 防止遍历后head指向表尾
    //遍历链表 得到表尾前一个  head->next为表尾 表尾的下一个为空
    while (i!=id)
    {
        head = head->next;
        id++;
    }

    head->next = head->next->next;//更改删除位置前一个地址的指向  
    head = h; //head存放的地址改为备份的表头
    while (head != NULL)
    {
        cout << head->val << " ";
        head = head->next;
    }//输出： 7 6 4 3
    return 0;
}

有序链表合并(力扣题)

输入：l1 = [1,2,4], l2 = [1,3,4]

输出：[1,1,2,3,4,4]

struct ListNode {
    int val;
    ListNode* next;
    ListNode() : val(0), next(nullptr) {}
    ListNode(int x) : val(x), next(nullptr) {}
    ListNode(int x, ListNode* next) : val(x), next(next) {}
    
};

//输入两个链表l1、l2 
//比较来自两个表节点的val 谁小就
ListNode* mergeTwoLists(ListNode* l1, ListNode* l2)
{
    ListNode* head = nullptr, * tail = nullptr;//定义新表头head   在新的链表中迭代的表节点tail

    //只要有一个不为空就执行(最多一个为空) 需要判断哪个不是空
    //如果表1是空 表2不是空  那么新表中只添加表2
    //如果表2是空 表1不是空 那么新表中只添加表2
    //如果都不是空 需要比较节点元素 添加
    while (l1 != nullptr || l2 != nullptr)
    {
        int a = (l1 != nullptr) ? l1->val : INT_MAX;//判断表1头val
        int b = (l2 != nullptr) ? l2->val : INT_MAX;//判断表2头val
        if (l1 == nullptr)
        {
            //表1是空 意味表2不是空
            //当head 尾空时意味着传入的l1是一个空 只需要l2也给到head即可
            if (head == nullptr)
            {
                head = l2;
                break;
            }
            else//当head不是空意味着 比较一部分后 表1已经没了 所以剩下只需要把新表的尾节点指向表2剩下的头即可
            {
                tail->next = l2;
                break;
            }
        }
        else if (l2 == nullptr)
        {
            //表2是空 意味表1不是空
            //当head 尾空时意味着传入的l2是一个空 只需要l1也给到head即可
            if (head == nullptr)//
            {
                head = l1;
                break;
            }
            else//当head不是空意味着 比较一部分后 表2已经没了 所以剩下只需要把新表的尾节点指向表1剩下的头即可
            {
                tail->next = l1;
                break;
            }
        }
        else//两个都不是空
        {
            if (a < b)//a小 就把表1的节点添加作为新表的下一个节点
            {
                if (head == nullptr)//head为空 表示才开始判断两个表头 需要给haed赋值
                {
                    tail = head = l1;
                }
                else//head不为空 只需要将新表表尾指向尾表1该节点 同时把新表表尾更改为表1该节点
                {
                    tail->next = l1;
                    tail = l1;
                }
                l1 = l1->next;//更新表1剩余首节点
                a = (l1 != nullptr) ? l1->val : INT_MAX;//同时更新a
            }
            else//与上面同理
            {
                if (head == nullptr)
                {
                    tail = head = l2;
                }
                else
                {
                    tail->next = l2;
                    tail = l2;
                }
                l2 = l2->next;//更新表2剩余首节点
                b = (l2 != nullptr) ? l2->val : INT_MAX;//同时更新b
            }
        }
    }
    return head;
}

int main() 
{
    ListNode* l1 = new  ListNode(1); 
    l1->next = new  ListNode(3); 
    l1->next->next = new  ListNode(9);
    l1->next->next->next = new  ListNode(11);

    ListNode* l2 = new  ListNode (2);
    l2->next= new  ListNode(4);
    l2->next->next = new  ListNode(6);
    l2->next->next->next = new  ListNode(8);
    ListNode* l = mergeTwoLists(l1, l2);

    while (l != NULL)
    {
        cout << l->val << " ";
        l = l->next;
    }//输出： 1 2 3 4 6 8 9 11

    return 0;
}

树

什么是树

一棵树是由n（n>0）个元素组成的有限集合，其中：

（1）每个元素称为结点（node）

（2）有一个特定的结点，称为根结点或树根（root）

（3）除根节点外，其余节点能分成m（m>=0）个互不相交的有限集合 T(0)-T(m-1)。其中的每一个子集都是一个树，这些集合被称为这棵树的子树。

如下图是一棵树：

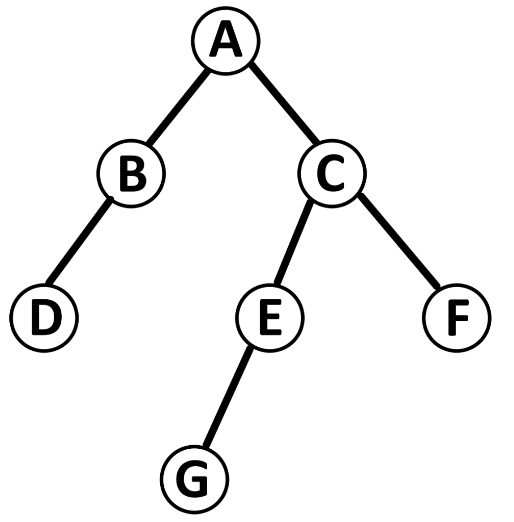
二叉树

二叉树：每个结点的子结点个数小于等于2.

满二叉树：每一层的节点数都达到最大值，且所有叶子节点都位于同一层。从图形上看，满二叉树的外观呈三角形。数学上讲，满二叉树各层节点数构成首项为1、公比为2的等比数列。深度为K的满二叉树总结点数为(2^K) - 1，且叶节点数等于2^(K-1)。如下图：

完全二叉树：在满二叉树的基础上，最后一层最右侧缺少n个连续节点

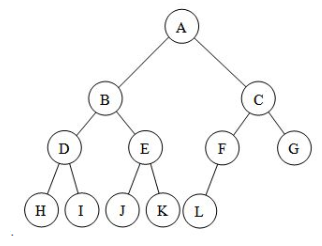
二叉树结构体的定义

二叉树在定义上与链表类似，树的每个结点有一个val成员和两个指针成员(指向左、右结点)

struct TreeNode 
{
      int val;//结点处的值
      TreeNode *left; //左节点 指针
      TreeNode *right;//右节点 指针
      TreeNode() : val(0), left(nullptr), right(nullptr) {}
      TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
      TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 };
//根据传参的不同，定义三种类型
// 1.无参： 值为0，左右节点地址为空NULL
// 2.只有元素参数： 值为指定参数，左右节点地址为空NULL
// 3.元素+地址：值为指定参数，左右节点地址为指定地址

二叉树的最大深度(力扣题)

给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。


//Definition for a binary tree node.
struct TreeNode {
      int val;
      TreeNode *left;
      TreeNode *right;
      TreeNode() : val(0), left(nullptr), right(nullptr) {}
      TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
      TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
  };

// 队列的初始输入为根节点 定义ans为得到的层数 sz为循环时该层节点
// 运用容器 存放树的每一层节点 对树的每一层遍历 依次判断该层每个节点是否有子节点
// 容器初始只有跟节点 如果队列不是空 那就ans++
// 判断完该层需要将队列迭代 将本层所有节点删除 然后存入该层节点的子节点存入
// 具体的操作做弹出队首赋值给变量 删除队首 判断变量是否有子节点 如果有 插入容器。
// 在此过程前需要求出容器长度 用来限定弹出节点数
// 循环执行 直到对前一层节点删除后容器为空

// 考虑到删除的节点与添加的子节点混淆 因此考虑队列 前删与后插
class Solution {
public:
    int maxDepth(TreeNode* root) 
    {
        if (root == nullptr) 
        {return 0;}
        queue<TreeNode*> Q;//创建队列
        Q.push(root);//添加树的根地址
        int ans = 0;
        TreeNode* node = NULL;
        while (!Q.empty()) 
        {
            int sz = Q.size();
            while (sz > 0) 
            {
                node = Q.front();//对首元素 
                Q.pop();//在队列中删除
                if (node->left) //判断弹出的是否有左子节点
                {
                    Q.push(node->left);//有左子节点 意味着有下一层
                }
                if (node->right) //判断弹出的是否有左子节点
                {
                    Q.push(node->right);
                }
                sz -= 1;
            }
            ans += 1;
        } 
        return ans;
    }
};

从前序与中序遍历序列构造二叉树(力扣题)

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

二叉树三种遍历方式：先序、中序、后序，其中先中后是形容根节点所在位置。

先序遍历：[ 根节点, [左子树的前序遍历结果], [右子树的前序遍历结果] ]

中序遍历：[ [左子树的中序遍历结果], 根节点, [右子树的中序遍历结果] ]

后序遍历：[ [左子树的后序遍历结果], [右子树的后序遍历结果]，根节点,]

其中在左子树和右子树中，仍然按照X序遍历排布

如下图先序遍历为：[3,9,20,15,7] 在这里3是根、9是左子树、[20,15,7]是右子树，而右子树也是按照先序遍历排布的20为右子树的根，15为左节点，7为右节点。

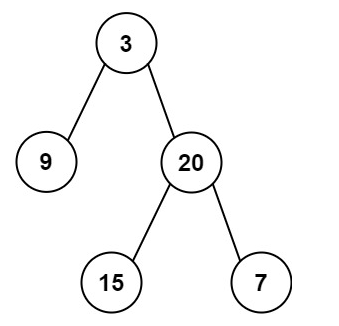
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]

输出: [3,9,20,null,null,15,7]

输入: preorder = [-1], inorder = [-1]

输出: [-1]

class Solution {
public:
    unordered_map<int, int> index;
    TreeNode* myBuildTree(const vector<int>& preorder, const vector<int>& inorder, 
int preorder_left, int preorder_right, int inorder_left, int inorder_right) 
 //左子树 右子树  左子树的边界 右子树的边界
    {
        if (preorder_left > preorder_right ) //左边界大于右边界 不构成区间
        {
            return nullptr;
        }
        //根节点的数字
        int rootval =preorder[preorder_left];

        // 在中序遍历中定位根节点
        int inorder_root = index[rootval];
        
        // 先把根节点建立出来
        TreeNode* root = new TreeNode(rootval);
        // 得到左子树中的节点数目
        int size_left_subtree = inorder_root - inorder_left;
        // 递归地构造左子树，并连接到根节点
        // 先序遍历中「从 左边界+1 开始的 size_left_subtree」个元素就对应了中序遍历中「从 左边界 开始到 根节点定位-1」的元素
        root->left = myBuildTree(preorder, inorder, preorder_left + 1, preorder_left + size_left_subtree, inorder_left, inorder_root - 1);
        // 递归地构造右子树，并连接到根节点
        // 先序遍历中「从 左边界+1+左子树节点数目 开始到 右边界」的元素就对应了中序遍历中「从 根节点定位+1 到 右边界」的元素
        root->right = myBuildTree(preorder, inorder, preorder_left + size_left_subtree + 1, preorder_right, inorder_root + 1, inorder_right);
        return root;
    }

    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) 
    {
        int n = preorder.size();
        //将每个节点在中序遍历的位置找到
        for (int i = 0; i < n; ++i) 
        {
            index[inorder[i]] = i;
        }
        return myBuildTree(preorder, inorder, 0, n - 1, 0, n - 1);
                       //左子树 右子树  左子树的边界 右子树的边界
    }
};

求根节点到叶节点数字之和(力扣题)

给你一个二叉树的根节点 root ，树中每个节点都存放有一个 0 到 9 之间的数字。

每条从根节点到叶节点的路径都代表一个数字：

例如，从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。

计算从根节点到叶节点生成的 所有数字之和 。

叶节点 是指没有子节点的节点。

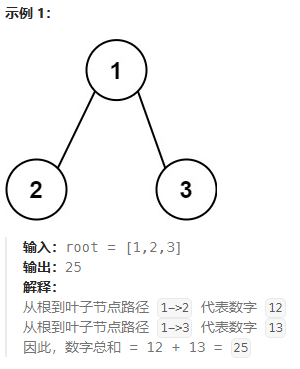
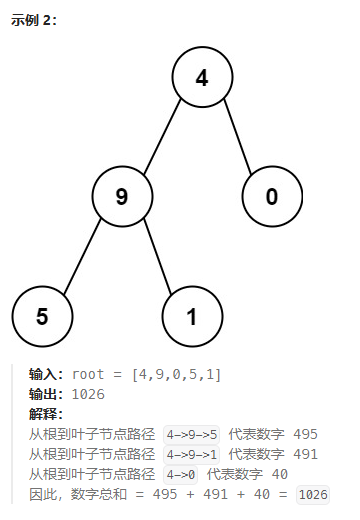
//类成员函数 输入是根节点
//整体思想采用求最大深度题的思想 
//只不过在将子节点加入到队列之前将子节点的值更新为（节点->val）*10+(子节点->val)
//当节点为叶子节点(无子节点)时，将叶子节点的val与num相加，
//num初始值为0
class Solution {
public:
    int sumNumbers(TreeNode* root) 
    {
        // 树为空 之和为0
        if(root== NULL)
        {
            return 0;
        }
        // 只有根 和为根->val
        if( root->left==NULL && root->right==NULL)
        {
            return root->val;
        }
        //存在子节点
        int num=0;
        list<int> list;
        queue<TreeNode*> Q;
        Q.push(root);
        TreeNode *node= NILL
        while( !Q.empty() )
        {
            int len=Q.size();
            while( len>0 )
            {
                node = Q.front();
                Q.pop();
                //当该节点无子节点时，将该节点val存入list中
                if( node->left==NULL && node->right==NULL )
                {
                    num=num+node->val;
                }
                else//该节点存在子节点
                {
                    if(node->left)//存在左子节点
                    {   //将该左子节点的val变为 节点val*10+左子节点val
                        node->left->val = node->left->val+ node->val*10 ;
                        Q.push(node->left);
                    }
                    
                    if(node->right)//存在右子节点
                    {   //将该右子节点的val变为 节点val*10+右子节点val
                        node->right->val = node->right->val+ node->val*10 ;
                        Q.push(node->right);
                    }
                }
                len--;
            }
        }
        return num;
    }
};