区间动态规划问题

学习动规的第二篇笔记     (≖ᴗ≖)✧

石子合并1：

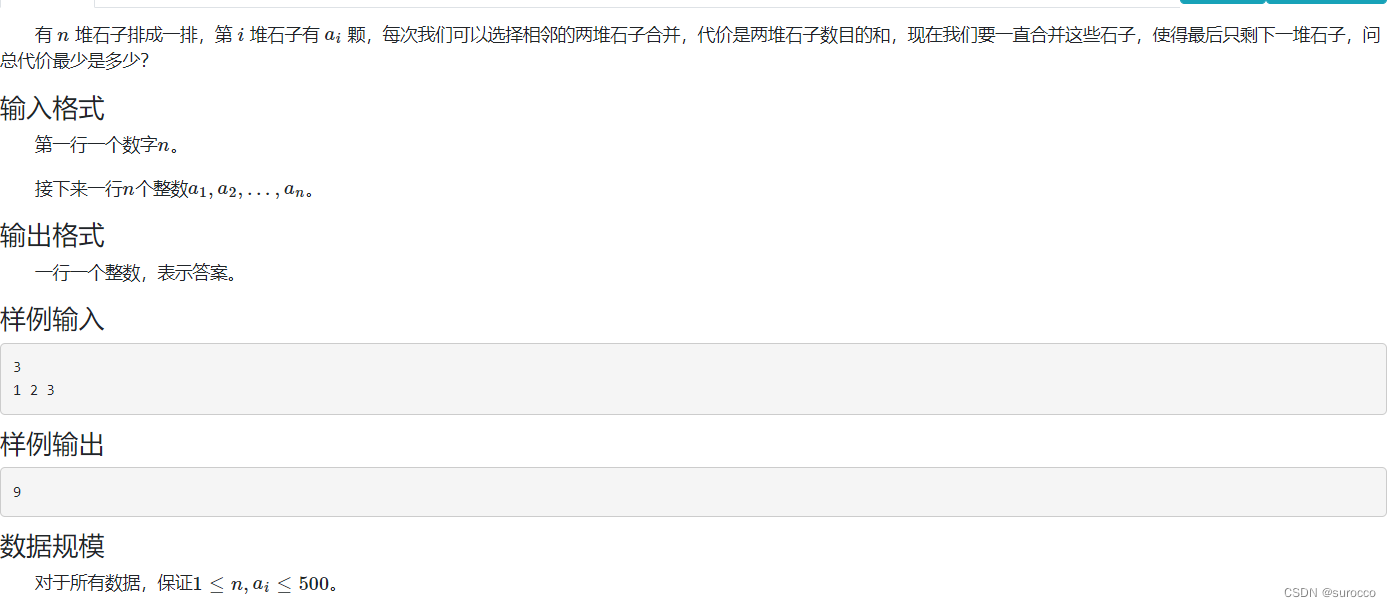
 递归做法:

要把两堆石子合并成一堆石子，一定存在一个分界线 x，使得两堆石子中的一堆是初始第 1 堆到第 x 堆石子合并得到的结果，另一堆是初始第 x + 1 堆到第 n 堆石子合并得到的结果。那么f[l][r]就等于前一部分合并需要的代价加上后一部分合并需要的代价加上这两部分合并需要的代价，两部分合并需要的代价也就是a[l]到a[r]的总和；

然后直接递归处理就可以了

可以用前缀和求一下a[l]到a[r]的和，另外，由于f[l][r]在本题中被多次计算，所以要再使用记忆化数组处理一下

int a[510], sum[510];
int f[510][510];
int solve(int l, int r) {
	if (l == r) return 0;
	if (f[l][r]) return f[l][r];
	int ans = INF;
	for (int i = l; i < r; i++) 
		ans = min(ans, solve(l, i) + solve(i + 1, r));
	f[l][r] = ans + sum[r] - sum[l - 1];
	return f[l][r];
}
int main() {
	int n;
	cin >> n;
	for (int i = 1; i <= n; i++) {
		cin >> a[i];
		sum[i] = a[i] + sum[i - 1];
	}
	int ans = solve(1, n);
	cout << ans << endl;
	return  0;
}

动规做法：

用 dp[i][j] 表示合并区间 [i, j] 的最小代价；

与递归思想一样，得出状态转移方程为dp[i][j] = min(dp[i][j], dp[i][k] + dp[k + 1][j] + sum[j] - sum[i - 1]);

具体怎么实现呢？

因为在求解dp[i][j]时，需要知道dp[i][k]和dp[k + 1][j]的值，也就是在求解一段区间时，我们要预先知道比它长度更小的区间的值，所以我们按照区间从小到大计算。

int a[510], sum[510];
int dp[510][510];//用dp[i][j]表示合并区间i,j的最小代价
int main() {
	int n;
	cin >> n;
	for (int i = 1; i <= n; i++) {
		cin >> a[i];
		sum[i] = sum[i - 1] + a[i];
	}
	memset(dp, 127, sizeof(dp));//初始化为无穷大
	for (int i = 1; i <= n; i++) dp[i][i] = 0;
	for(int i=1;i<n;i++)//区间长度r-l
		for (int j = 1; j <= n-i; j++) //枚举区间左端点
			for (int k = j; k <j + i ; k++) //枚举分隔点
				dp[j][j + i] = min(dp[j][j + i], dp[j][k] + dp[k + 1][j + i] + sum[j + i] - sum[j - 1]);
	cout << dp[1][n] << endl;
	return 0;
}

 括号序列

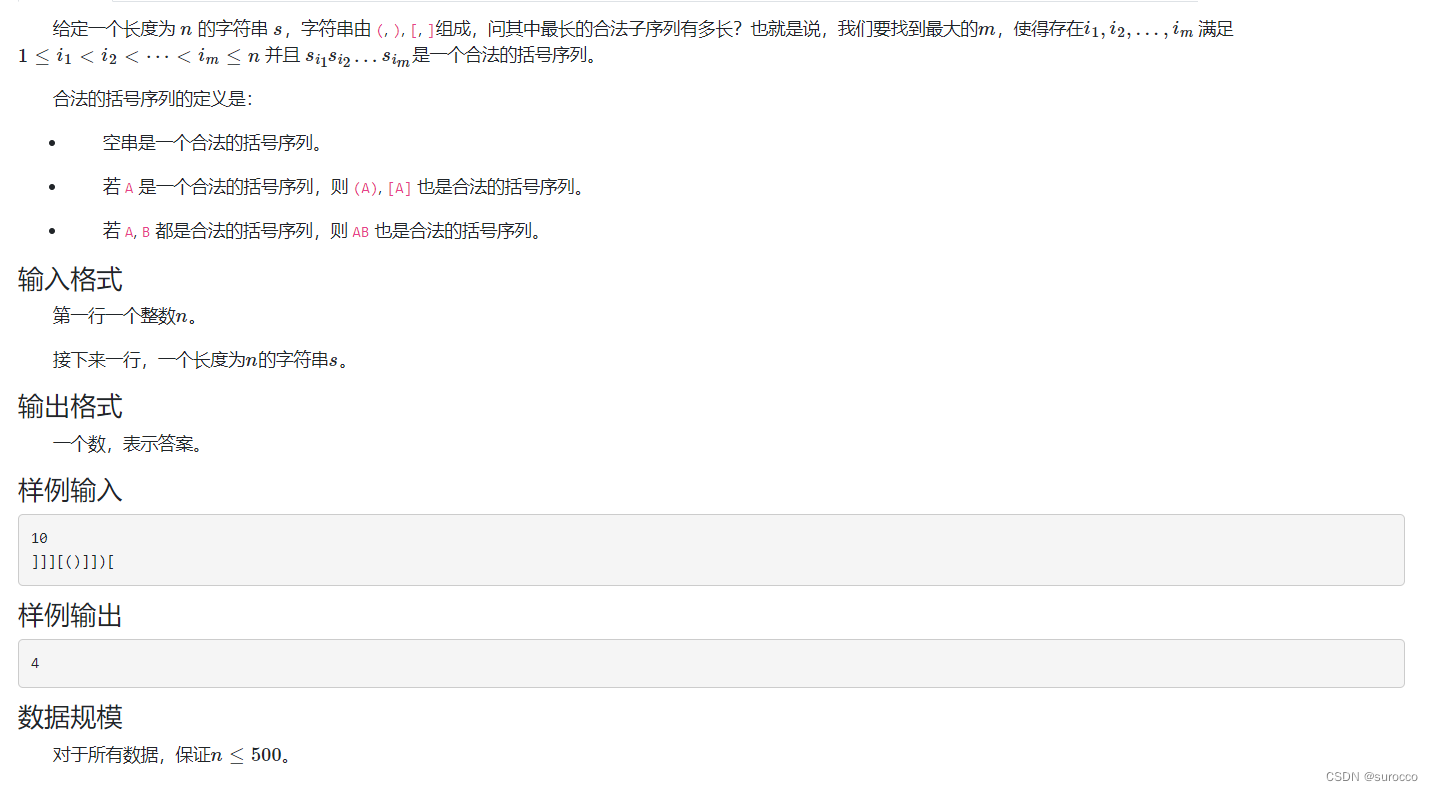
用 f[i][j] 表示 s中下标i到j 中最长的合法子序列的长度；

转移：

• f[i][j] = max(f[i][j], f[i + 1][j])
• f[i][j] = max(f[i][j], f[i][j - 1])
• 如果s[i]和s[j] 匹配，f[i][j] = max(f[i][j], f[i + 1][j - 1] + 2)
• 枚举分界线 k，f[i][j] = max(f[i][j], f[i][k] + f[k + 1][j])

但是1和2已经被包含在4中了，所以只需要考虑两端是否相等，然后枚举分隔线即可
 

int f[510][510];
int main() {
	int n;
	string s;
	cin >> n >> s;
	for (int i = 1; i < n; i++) {//区间长度r-l
		for (int j = 0; j < n-i; j++) {//区间左端点
			if ((s[j] == '(' && s[j + i] == ')') || s[j] == '[' && s[j + i] == ']') f[j][j + i] = f[j + 1][j + i - 1] + 2;
			for (int k = j; k <= i + j; k++) {
				f[j][j + i] = max(f[j][j + i], f[j][k] + f[k + 1][j + i]);
			}
		}
	}
	cout << f[0][s.size() - 1];
	return 0;
}

 石子合并2

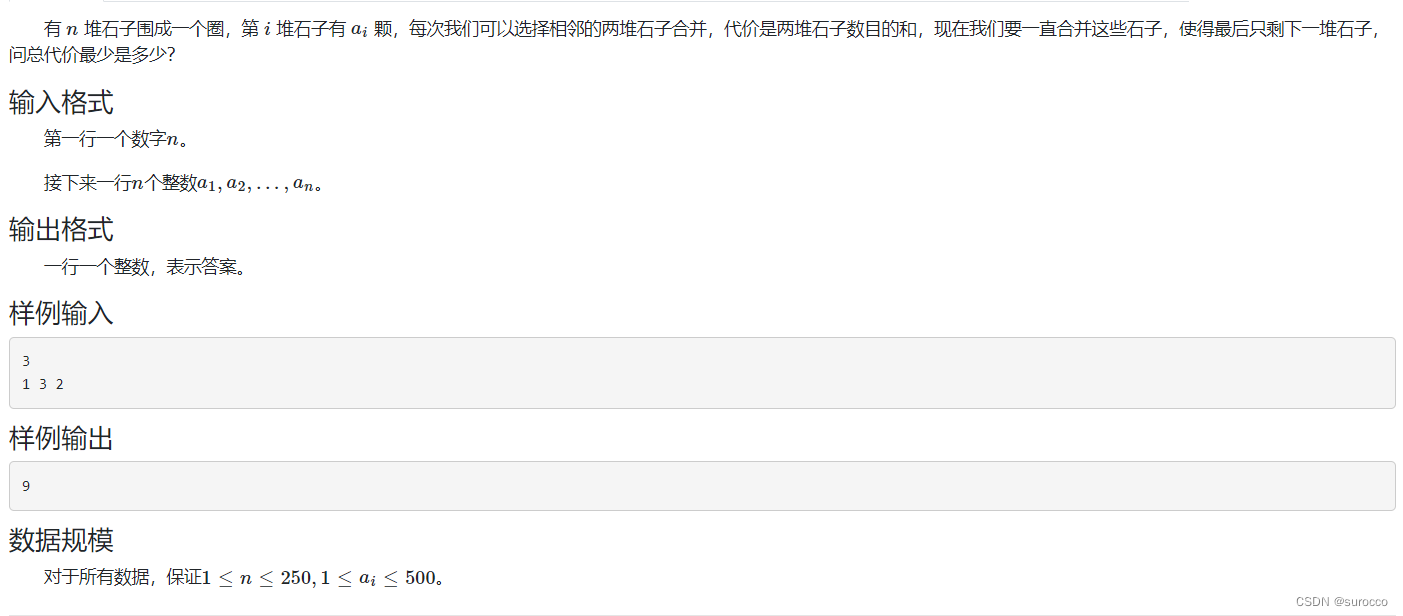
 这个题和石子合并1的区别就是变成了一个环

考虑一开始的圆，圆上有 n 堆石子，在相邻的石子间连边，一共有 n 条边。每次合并相邻两堆石子的时候，有一条边会消失。从开始到结束一共要合并 n - 1 次，有 n - 1 条边会消失，也就是说最后一定会有一条边没有消失。

因为有一条边最后没有消失，我们可以理解成这条边一开始就不存在，现在只剩下了 n - 1 条边，问题变成了一条链的情况，这时就和石子合并问题一模一样了

然后我们 直接枚举没有消失的边即可。

但是这样做的时间复杂度是O(n^4)，考虑优化

构造一个长度为 2n 的序列，由两个 a 数组连接起来得到，对于这个长度为2n的序列，做石子合并1中的dp操作，那么最后, f[1][n]表示消失的是第 n 堆和第 1 堆石子之间的边，f[2][n + 1]表示消失的是第 1 堆和第 2 堆石子之间的边，f[3][n + 2]消失的是第 2 堆和第 3 堆石子之间的边……

直接对 f[1][n]，f[2][n + 1]，f[3][n + 2]……这些取最小值即可。（妙，实在太妙了 ）

int a[510], sum[510];
int dp[510][510];//用dp[i][j]表示合并区间i,j的最小代价
int main() {
	int n;
	cin >> n;
	for (int i = 1; i <= n; i++) {
		cin >> a[i];
		sum[i] = sum[i - 1] + a[i];
	}
	for (int i = n + 1; i <= 2 * n; i++) {
		a[i] = a[i - n];
		sum[i] = sum[i - 1] + a[i];
	}
	memset(dp, 127, sizeof(dp));
	for (int i = 1; i <= n*2; i++) dp[i][i] = 0;
	for (int i = 1; i < n*2; i++)//区间长度r-l
		for (int j = 1; j <= n*2 - i; j++) //区间左端点
			for (int k = j; k < j + i; k++)
				dp[j][j + i] = min(dp[j][j + i], dp[j][k] + dp[k + 1][j + i] + sum[j + i] - sum[j - 1]);
	int ans = INF;
	for (int i = 1; i <= n; i++) {
		ans = min(ans, dp[i][n + i - 1]);
	}
	cout << ans << endl;
	return 0;
}