递推法:
递推法是一种在数学和其他领域广泛应用的重要方法,它在计算机科学中被用作一种关键的数值求解算法。
知识点:
- 递推算法
- 递归算法
递推算法的特点
递推法的核心在于找到递推关系式。这种方法可以将复杂的计算过程转化为简单的重复步骤,充分利用计算机在运行程序时的时间局部性和空间局部性。
递推算法的思想
- 首先找到各个相邻数据项之间的递推关系;
- 递推关系避开了求通项公式的麻烦,尤其是对于那些难以或无法求解通项公式的题目;
- 将复杂问题分解为若干步骤的简单运算;
- 一般来说,递推算法可以视为一种特殊的迭代算法。
递推算法解题的基本思路
- 将复杂计算转换为简单重复运算;
- 通过找到递推关系式进行简化运算;
- 利用计算机的特性,减少运行时间。
递推算法的一般步骤
- 根据题目确定数据项,并找到符合要求的递推关系式;
- 根据递推关系式设计递推程序;
- 根据题目找到递推的终点;
- 单次查询可以不进行存储,多次查询都要进行存储;
- 按要求输出答案即可。
递归算法
递归算法是一种自顶向下的算法,它通过不断地直接或间接调用自身的函数,通过每次改变变量完成多个过程的重复计算,直到到达边界之后,结束调用。
与递推法相似的是,递归与递推都是将一个复杂过程分解为几个简单重复步骤进行计算。
递归算法的实现的核心是分治策略,即分而治之,将复杂过程分解为规模较小的同类问题,通过解决若干个小问题,进而解决整个复杂问题。
递归算法的思想
- 将复杂计算过程转换为简单重复子过程;
- 找到递归公式,即能够将大问题转化为小问题的公式;
- 自上而下计算,在返回完成递归过程。
递归算法设计的一般步骤
- 根据题目设计递归函数中的运算部分;
- 根据题目找到递归公式,题目可能会隐含给出,也可能需要自己进行推导;
- 找到递归出口,即递归的终止条件。
递归法和递推法的思路已经给大家讲解得差不多了,接下来我们将结合真实的大赛题目进行讲解。这将有助于我们更好地理解和应用这两种方法。
斐波纳契数列 fibonacci 问题
在一定情况下,同一个问题可以使用用递归也可以使用递推解答。一般一个问题的递推关系和递归关系都好求的话就都可以解题。
当然如果题目只有一个关系好求,那就最好采用关系好求的办法。
题目描述:
斐波那契数列(Fibonacci sequence),又称黄金分割数列,因数学家莱昂纳多·斐波那契(Leonardoda Fibonacci)以兔子繁殖为例子而引入,故又称为“兔子数列”。
指的是这样一个数列:0、1、1、2、3、5、8、13、21、34、…0
在数学上,斐波那契数列以如下被以递推的方法定义:F(0)=0,F(1)=1,F(n)=F(n−1)+F(n−2)(n≥2,n∈N∗)
请求出该数列中第 n 个数字(n 从11开始计数)是多少。
样例:
输入样例
样例1输入
6
样例2输入
4
输出样例
样例1输出
8
样例2输出
3
对于上面的样例我们进行了如下计算;
[0]=0
[1]=1
[2]=0+1
[3]=1+1=2
[4]=1+2=3
[5]=2+3=5
[6]=5+3=8
运行限制:
1. 最大运行时间:1s
2. 最大运行内存:128M
题目解析:
- 这个题给出递推式 F(n)=F(n−1)+F(n−2)
- 转化为可用的递推关系,即F(n)+F(n+1)=F(n+2)
这一通过从 n=1 开始循环即可完成递推,当然也可以使用递归法。
首先我们写找出递归式,F(n)=F(n−1)+F(n−2)。
F(n)= F(n-1) + F(n-2)
= F(n-2)+F(n-3)+F(n-3)+F(n-4)
//重复调用
这样我们找到了递归式,然后我们应该找到递归出口。
我们可以知道 F(n)=0n=0,F(n)=1n=1 这就是递归出口,能让递归停止的条件。
递归算法的通用框架如下:
do(a,b,c...)
{
//递归终止条件,即出口
if(a==? ,b==? ,....) return
//递归条件
if(条件1)
do(参数1)
else(条件2)
do(参数2)
}
如本题,各子式间存在计算关系,可以化为:
do(a)
{
if(a==0) return 0;
if(a==1) return 1;
return do(a-1)+do(a-2);
}
这道题不是多次询问问题,不需要存储直接计算的复杂度是最低的。
答案解析
C++ 代码:
- 递推算法代码
#include <iostream>
using namespace std;
int main()
{
int n; //第几个数
int x=0; //F(n)
int y=1; //F(n+1)
int ans; //F(n+2)
cin>>n;
if(n==0) ans=0;
else if(n==1) ans=1;
else {
for(int i=2;i<=n;i++)
{
ans=x+y;
x=y;
y=ans;
}
}
cout<<ans<<endl;
}
- 递归算法代码
#include <iostream>
using namespace std;
int fn(int n)
{
//递归出口1
if(n==0)
return 0;
//递归出口2
else if(n==1 )
return 1;
else
return fn(n-1)+fn(n-2); //递归关系式
}
int main()
{
int n; //第几个数
int ans;
cin>>n;
ans=fn(n);
cout<<ans<<endl;
}
Python 解题代码
- 递推算法代码:
if __name__ == '__main__':
n =int( input())
x=0 # F(n)
y=1 #F(n+1)
ans=0 #F(n+2)
if n==0 :
ans=0
elif n==1:
ans=1
else:
for i in range (n-1):
ans=x+y
x=y
y=ans
print(ans)
- 递归算法代码:
def f(n):
# 递归出口1
if n == 0:
return 0
# 递归出口2
elif n == 1:
return 1
else:
return f(n - 1) + f(n - 2) # 递归关系式
if __name__ == '__main__':
n = int(input())
ans = f(n)
print(ans)
Java 解题代码
递推算法:
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
int n; //第几个数
int x=0; //F(n)
int y=1; //F(n+1)
int ans = 0; //F(n+2)
Scanner in = new Scanner(System.in);
n = in.nextInt();
if(n==0) ans=0;
else if(n==1) ans=1;
else {
for(int i=2;i<=n;i++)
{
ans=x+y;
x=y;
y=ans;
}
}
System.out.println(ans);
}
}
递归算法代码:
import java.util.Scanner;
public class Main {
static int fn(int n)
{
if(n==0)
return 0;
//递归出口2
else if(n==1 )
return 1;
else
return fn(n-1)+fn(n-2); //递归关系式
}
public static void main(String[] args) {
int n; //第几个数
int ans = 0;
Scanner in = new Scanner(System.in);
n = in.nextInt();
ans=fn(n);
System.out.println(ans);
}
}
存储型的递推与递归
存储的方式适用于大部分的的多次查询问题。
题目描述:
斐波那契数列(Fibonacci sequence),又称黄金分割数列,因数学家莱昂纳多·斐波那契(Leonardoda Fibonacci)以兔子繁殖为例子而引入,故又称为“兔子数列”。
指的是这样一个数列:0、1、1、2、3、5、8、13、21、34、…
在数学上,斐波那契数列以如下被以递推的方法定义:F(0)=0,F(1)=1,F(n)=F(n−1)+F(n−2)(𝑛≥2,𝑛∈𝑁∗)
我们将进行M次查询,每次输入一个𝑁N,其中n小于3030。
请求出该数列中第n个数字(n从11开始计数)是多少?
样例:
输入样例
样例1输入:
6
4
2
7
8
8
10
样例2输入:
8
13
23
14
17
24
16
10
11
输出样例
样例1输出:
3
1
13
21
21
55
样例2输出:
233
28657
377
1597
46368
987
55
89
运行限制:
1. 最大运行时间:1s
2. 最大运行内存:128M
题目解析:
这道题跟上面一道题的算法原理相同,只是增加了多次查询的复杂度,所以仅需修改这一点即可。
再有的是有的同学担心自己的输入输出是在一个屏幕上的,评测的时候会不会出现问题。

类似这样的情况,这一点是不用担心的,只要不是交互题,评测机的输入与输出是分开的,只有你的输出会用来跟答案比较,所以我们只用关心我们的输出即可。
比如有一道题让你计算 x+y 的值,如果你知道每答案,就可以直接输出,都不用进行读入。
然后我们来看一下需要多次询问的题目该怎么解决。
答案解析
C++ 代码:
- 递推算法代码
#include <iostream>
using namespace std;
int F[35];
void init()
{
F[0]=0;
F[1]=1;
for(int i=2;i<=30;i++)
{
F[i]=F[i-1]+F[i-2];
}
}
int main()
{
int m; //m次查询
int n; //第几个数
init();
cin>>m;
while(m>0){
m-=1;
cin>>n;
cout<<F[n]<<endl;
}
}
存储答案的递推法,才是最常使用的递推法。
- 递归算法代码
#include <iostream>
using namespace std;
int F[35];
int fn(int n)
{
//递归出口1
if(n==0)
{
F[0]=0;
return 0;
}
//递归出口2
else if(n==1 )
{
F[1]=1;
return 1;
}
else
{
F[n]=fn(n-1)+fn(n-2);
return F[n]; //递归关系式
}
}
int main()
{
int m; //m次查询
int n; //第几个数
fn(30);
cin>>m;
while(m>0){
m-=1;
cin>>n;
cout<<F[n]<<endl;
}
}
Python 解题代码
递推算法代码:
F = [0]*35
def init():
F[0] = 0
F[1] = 1
for i in range(2, 30):
F[i] = F[i-1]+F[i-2]
if __name__ == '__main__':
m = int(input())
init()
while m > 0:
m -= 1
n = int(input())
print(F[n])
# print(F)
递归算法代码:
F = [0] * 35
def f(n):
# 递归出口1
if n == 0:
F[0] = 0
return 0
# 递归出口2
elif n == 1:
F[1] = 1
return 1
else:
F[n] = f(n - 1) + f(n - 2) # 递归关系式
return F[n]
if __name__ == '__main__':
m = int(input())
f(30)
while m > 0:
m -= 1
n = int(input())
print(F[n])
# print(F)
Java 解题代码
递推算法:
import java.util.Scanner;
public class Main {
static int []F=new int [35];
static void init()
{
F[0]=0;
F[1]=1;
for(int i=2;i<=30;i++)
{
F[i]=F[i-1]+F[i-2];
}
}
public static void main(String[] args) {
int m; //m次查询
int n; //第几个数
init();
Scanner in = new Scanner(System.in);
m = in.nextInt();
while(m>0){
m-=1;
n= in.nextInt();
System.out.println(F[n]);
}
}
}
递归算法代码:
package com.company;
import java.util.Scanner;
public class Main {
static int []F=new int [35];
static int fn(int n)
{
//递归出口1
if(n==0)
{
F[0]=0;
return 0;
}
//递归出口2
else if(n==1 )
{
F[1]=1;
return 1;
}
else
{
F[n]=fn(n-1)+fn(n-2);
return F[n]; //递归关系式
}
}
public static void main(String[] args) {
int m; //m次查询
int n; //第几个数
fn(30);
Scanner in = new Scanner(System.in);
m = in.nextInt();
while(m>0){
m-=1;
n= in.nextInt();
System.out.println(F[n]);
}
}
}
数字三角形问题
题目描述:
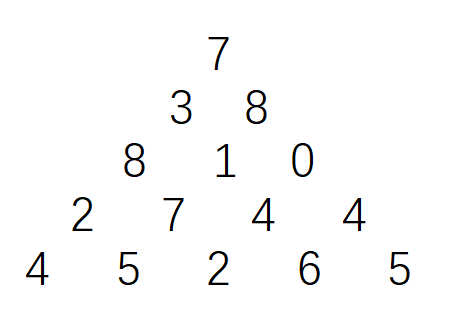
如图数字三角形。如下所示为一个数字三角形。请编一个程序计算从顶到底的某处的一条路径,使该路径所经过的数字总和最大。只要求输出总和。
- 一步可沿左斜线向下或右斜线向下走;
- 三角形行数小于等于 100100;
- 三角形中的数字为 0,1,…,990,1,…,99;
测试数据通过键盘逐行输入。
如上例数据应以样例所示格式输入:
样例:
输入:
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
输出:
30
运行限制:
1. 最大运行时间:1s
2. 最大运行内存:128M
题目分析:
解决该题目的方式有很多,包括动态规划, 枚举都可以解决这个问题。
我们从递推的思想出发,假设我们从顶层沿着某条路径已经走到了第 𝑖i 层,正向着 𝑖+1i+1 层前进, 两条可行路径中我们肯定会选择最大的方向前进,为此我们可以采用递推中的反向递推,即逆推的方式解决,设 𝑎[𝑖][𝑗]a[i][j] 存放从 𝑖,𝑗i,j 出发到达第 𝑛n 层的最大值。
我们可以写出递推式:
a[i][j] = max{a[i][j]+a[i+1][j],a[i][j]+a[i+1][j+1]}
则 逆推到出发点 a[1][1] 为题目所求答案,即第一层到第 𝑁N 层的最大值。
答案解析
C++ 代码:
#include<iostream>
using namespace std;
int main()
{
int n; //n层
int a[101][101]; //路径矩阵
cin>>n;
//输入数字三角形的值
for (int i=1; i<=n; i++)
{
for (int j=1; j<=i; j++)
{
cin>>a[i][j]; //输入原始数据
}
}
//递推开始
for (int i=n-1; i>=1; i--)//从最后一层逆推
{
for (int j=1; j<=i; j++)
{
if (a[i+1][j]>=a[i+1][j+1])
a[i][j]+=a[i+1][j]; //路径选择
else
a[i][j]+=a[i+1][j+1];
}
}
cout<<a[1][1]<<endl;
}
Python 解题代码
a = [[0] * 101] * 101
if __name__ == '__main__':
n = int(input())
# 输入数字三角形的值
for i in range(1, n+1):
a[i] = input().split()
a[i] = list(map(int, a[i])) # split 分割后都是 字符 这里是转化成数字
#
# for i in range(1, n + 1):
# print(a[i])
# a = list(map(int, a)) # split 分割后都是 字符 这里是转化成数字
# 递推开始
for i in range(n - 1, 0, -1):
# 最后一层逆推
for j in range(0, i):
# 路径选择
if a[i + 1][j] >= a[i + 1][j + 1]:
a[i][j] += a[i + 1][j]
else:
a[i][j] += a[i + 1][j + 1]
# for i in range(1, n + 1):
# print(a[i])
print(a[1][0])
Java 解题代码
package com.company;
import java.util.Scanner;
public class Main {
static int [][]a=new int [101][101];
public static void main(String[] args) {
int n;
Scanner in = new Scanner(System.in);
n = in.nextInt();
//输入数字三角形的值
for (int i=1; i<=n; i++)
{
for (int j=1; j<=i; j++)
{
a[i][j]=in.nextInt(); //输入原始数据
}
}
//递推开始
for (int i=n-1; i>=1; i--)//从最后一层逆推
{
for (int j=1; j<=i; j++)
{
if (a[i+1][j]>=a[i+1][j+1])
a[i][j]+=a[i+1][j]; //路径选择
else a[i][j]+=a[i+1][j+1];
}
}
System.out.println(a[1][1]);
}
}























 421
421

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








