C语言函数递归例题讲解（超详细~）

递归题型讲解:

例题1

那根据下面递归函数：调用函数Fun(2)，返回值是多少（ ）

int Fun(int n)      
{ 
  if(n==5)   
    return 2;     
  else     
    return 2*Fun(n+1);      
}

A.2
B.4
C.8
D.16

首先我们先画个图~

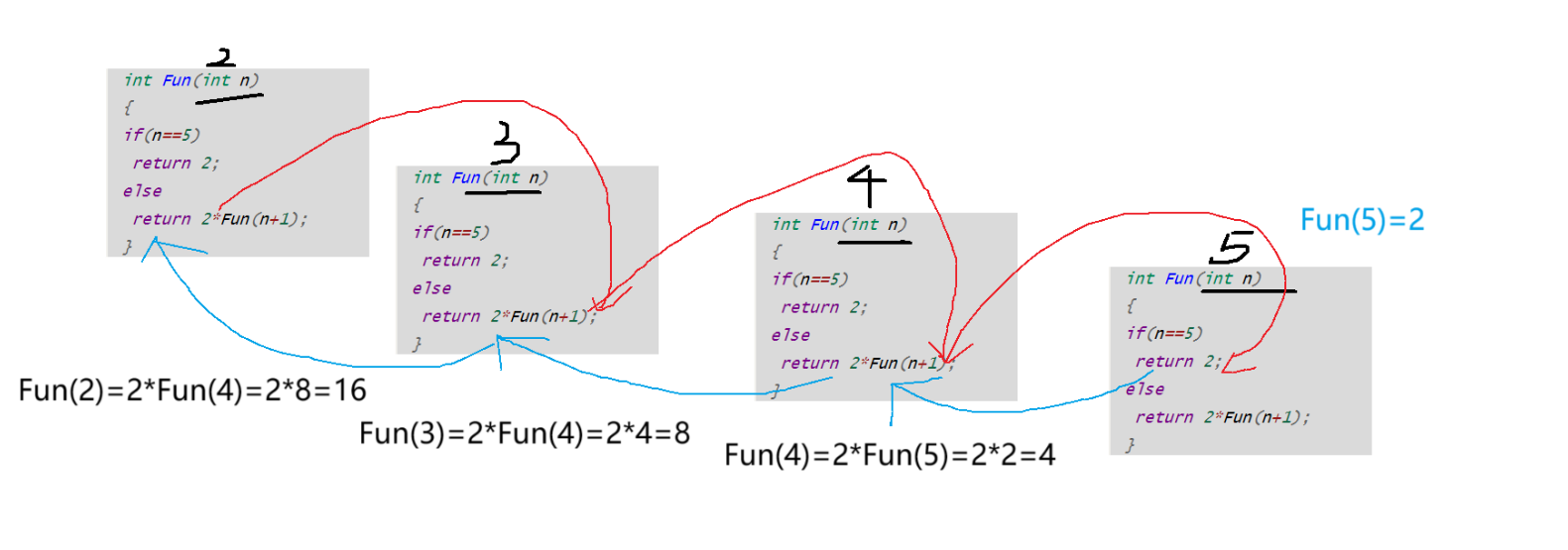
题目分析：

由图我们可以看出，当我们要求Fun(2)的值时，程序会先进入到else的那层分支语句里面，然后逐层递推下去，直到n==5时，返回2，也就是Fun(5)=2,然后就逐层往上回归，这样我们就能求得出Fun(2)=16。

因此这题我们应该选D。

例题2

递归实现n的k次方

​ 题目分析：

首先，我们举个例子，我们这里要求3的4次方，那我们是不是可以写成3x3x3^(4-1),括号里面的4指的是k,也就是说这个n的值是固定的，k的值会随着函数递推下去而逐渐减少，因此我们可以写成n*Pow(n,k-1),那么这个递归的终止条件是什么呢，细心的话，我们可以发现当k=1时， 3^1=3，则返回的是n它本身的值，也就是return n。当k=0时，3^0=1。也就是说返回的值是1，那么就是return 1。

根据上述例子，我们就能写出相对应的代码出来：

#include <stdio.h>

int Pow(int n,int k)	
{
	if(k==0)
		return 1;
	else if(k==1)
		return n;
	else
		return n*Pow(n,k-1);

}

int main()
{
	int n=3;
	int k=4;
	printf("%d\n",Pow(n,k));
	return 0;
}

运行结果如下所示：

除此之外
我们再细看一下这个递归图：

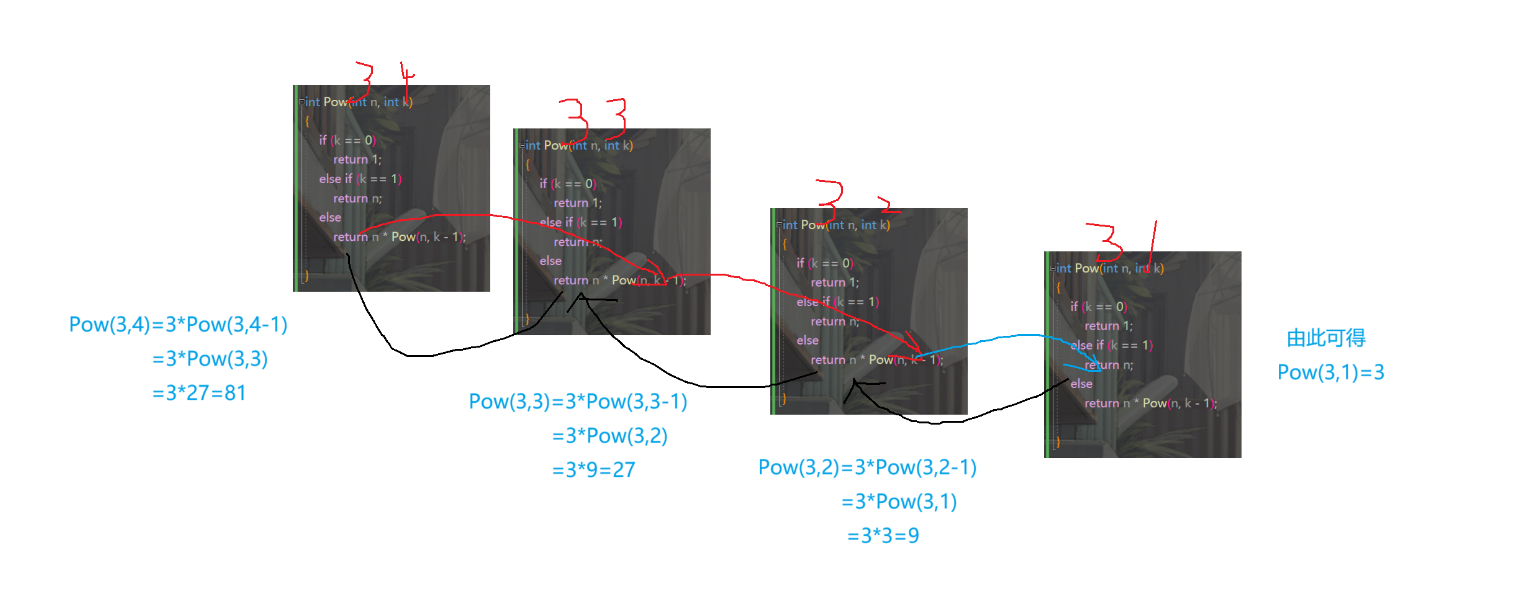
从图中我们可以看出当k的值为1时返回的是3，然后再逐层往上回归，直到我们把Pow(3,4)的值求出来，那么递归才结束。

例题3

计算一个数的每位之和（递归实现）

写一个递归函数DigitSum(n)，输入一个非负整数，返回组成它的数字之和

例如，调用DigitSum(1729)，则应该返回1+7+2+9，它的和是19

输入：1729，输出：19

题目分析：

首先，根据题干信息，我们发现当我们传一个非负整数n过去的时候，在函数DigitSum(n)内部，我们可以分两种情况进行分析，比如当n的值小于等于9的时候，我们就直接return n就可以了，当n的值大于等于10的时候，我们可以先用n%10求得每一位的余数，然后再加上DigitSum(n/10)这个条件，合起来也就是return n%10+DigitSum(n/10),并且我们还要想一下这个递归终止条件是什么？细心的话可以发现，随着n的值不断/10,直到n的值除到个位数的时候，返回n的值，然后在逐一往上层回归，最终就能求出它每一位数的和出来。

另外
我们把这个递归展开图给大家看一下：

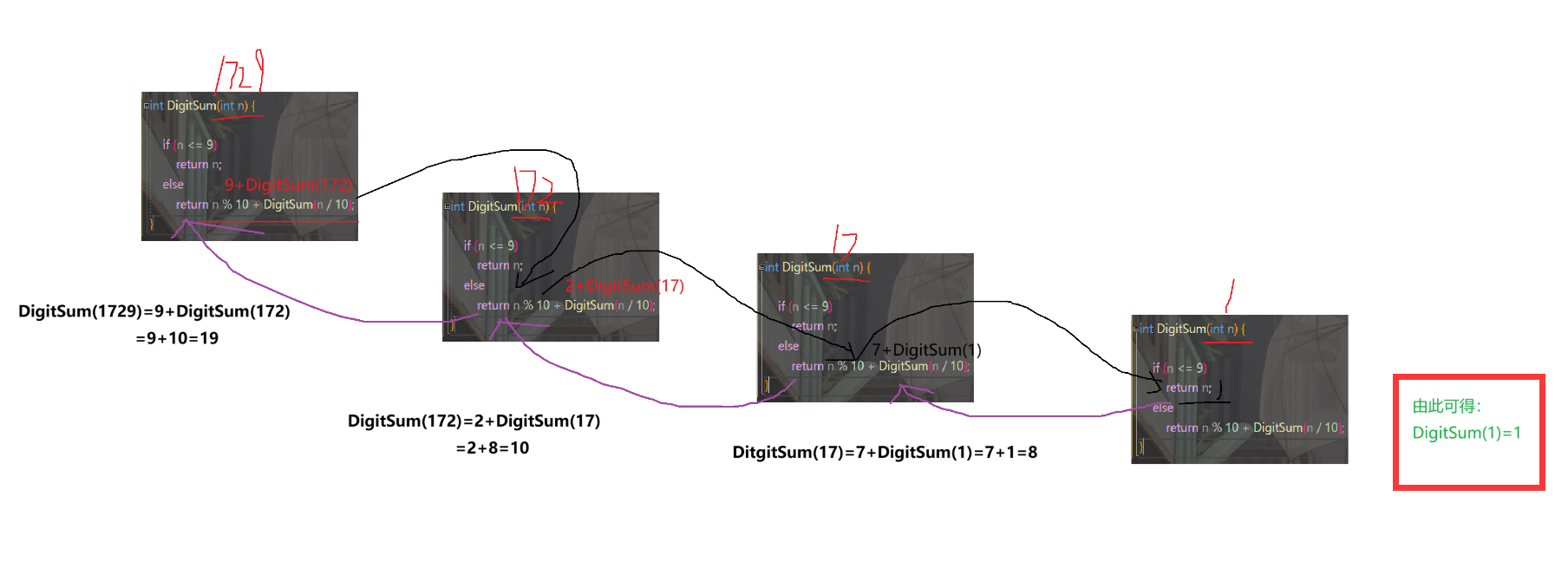
由图中我们可以看出，当用户输入1729的值后，函数将层层递推下去，直到n的值少于10，也就是DigitSum(1)时，返回的值为1，接着又向上层层回归上去，并且把该层n%10的值和上一层n的值累加起来，最后我们就能求出DigitSum(1729)=19。

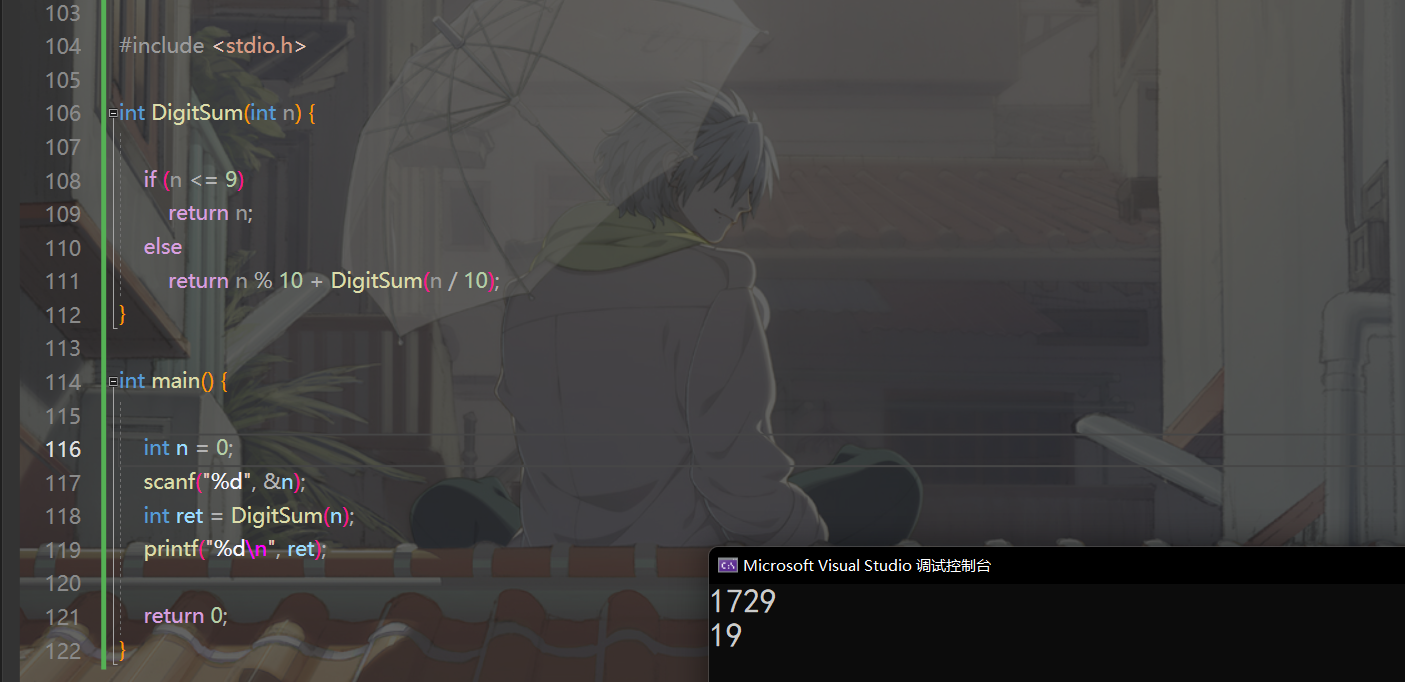
下面我们来看一下这道题代码的实现部分以及效果图：

#include <stdio.h>

int DigitSum(int n) {

	if (n <= 9)
		return n;
	else
		return n % 10 + DigitSum(n/10);
}

int main() {

	int n = 0;
	scanf("%d",&n);
	int ret = DigitSum(n);
	printf("%d\n", ret);

	return 0;
}

好了，本期的分享到这里就结束啦！希望大家都能掌握递归的例题。

可以的话，能给博主一个三连可以吗，谢谢！！！