思路:
求的是所有从1~n的路径当中先买再卖的最大的收益。求的是每个方案差价的最大价值。然后我们可以将所有路径看作一个集合,然后将其进行集合的划分,做到不重不漏即可,然后从所有子集的最大值里,比较得出最大的那个!即先是乡镇选拔,后面再是县选拔,再到市里选拔!
分成子集:
第一个子集可以是表示为所有从第一个点前面买,第一个后面卖的所有路径里所获得价值最大的那条路径。所以说买和卖的分界点是1号点,以此类推,则每个集合都以这样来进行划分。
所以说:以某个点来做为买和卖的分界点,而分界点这个位置也是可以卖和买的。所有1号点可以做为分界点这样的路线归为第一类,所有2号点可以做为分界点的归为第二类。依次类推。
所以这样的划分方式,一定可以把所有的方案全部枚举到,每一类分别取一个最大值,最后取一个max,即可得到全部的最大值了。
如何求某一类的最大值:
假设求的是第k类,所有以k为分界点的,即在k前面买,在k后面卖的所有路径的集合里的最大价值。我们需要分段求:
- 从1走到k买入的最小值。d_min[k]
- 从k走到n卖出的最大值。d_max[k];
- 只要能求出:d_min[k] 和 d_max[k],就能求出最大的差价了!这样做的正确性证明:因为从1~k和从k ~ n是两段独立的。每个城市都可以经过若干次。分别让左边取一个min,右边取一个max就可以了!
先求d_min(K);
然后对于假设转移到第k个点有t种转移方式,假设分别是:s1, s2, ,st; 则又可以划分为t个子集,然后可得 d_min(k) = min{d_min(s1), d_min(s2), … d_min(st), w[k] }; 虽然本质是DP的过程,但是题目中可能存在环,因此就不能用DP来做了,但可以转化为最短路模型来做。而最短路而言有Dijkstra算法和Spfa算法,至于用哪种,要从算法的原理出发:
4. Dijkstra算法本质:每次从堆中取出来的最小值,如果能断定取出来的最小值已经不能被其他点更新的时候,那么就能用Dijkstra算法。而本题中,一个点可能会被多次更新: 如图: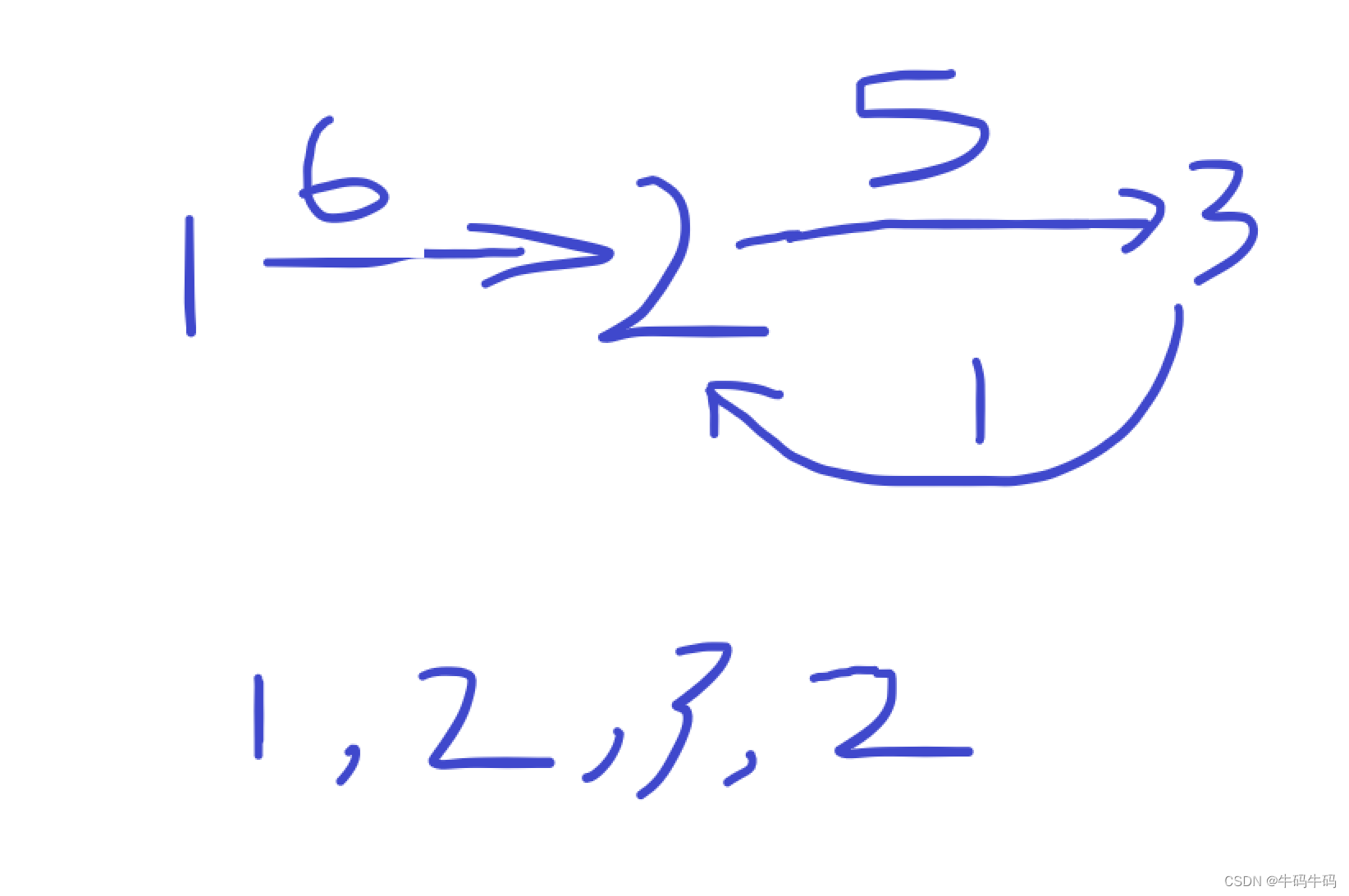
不难发现,图中的2被更新了两次,显然不符合,所以不能用Dijkstra算法!而可以用SPFA算法啊,因为Spfa算法一般来说都是正确的,因为适用性很广,其本质是Bellman-Ford算法。其本质类似于一个Dp问题,首先spfa和bellman是等价的。
bellman算法流程:
- for循环 迭代n-1次!每次迭代相当于求了所有经过一条边的最短距离,而最多只有n-1条边。因为当有n-1条边的时候,意味着所有的点都包含在这个路径当中了,因此整个最小值都求出来了,所以说最多只需要更新n-1次,就可以把所有长度是n-1的路径给找出来,即把所有经过n-1条边的路径找出来,而路径长度最多就是n-1,所以可以正确处理该问题,它是基于边数来考虑。即求的是所有经过k条边的最短路。
- for循环所有边,用三角不等式更新!
- 本质是一个动态规划的思想:当我们迭代了k次后,我们想求出来的是所有边数不超过K的最短路径,而由于我们已经求出来了所有长度不超过K-1条边的最短路径,所有长度不超过k的都是可以由不超过k-1的延申过来。和权值在点上或者边上没有关系!
所以说可以用d_min的值,对于d_max而言也是一样的,只需要把所有的边反向,建立一个反向图,然后从n号点出发求一个最大值就行了,此时k为终点,倒着模拟1~k求d_min来思考!两者是类似的。
求出来d_min和d_max后,再枚举下所有的分界点k,计算下d_min - d_max的最大值即为答案!
注意:
-
我们要分别求出同一个点的dmin和dmax,所以说spfa需要跑两遍,一遍针对max,一遍min,不过注意的是:两个可以合并到一起来写;下面给出了分开写和合并写的写法;
-
递推式:d[i] = min(d[j], w[i]) 本题求的是在哪个城市买卖,所以如果求买的话,买入最小,即为同一条边上的两个城市比较取min,而dist[j]是在i城市之前的所有城市里的最小买入,和第i座城市进行比较。反之对于求max也是一样的迭代!
-
另外还给出了dfs深度优先搜索的解法;
代码:
两次spfa:
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <queue>
using namespace std;
const int N = 1e5 + 10, M = 2e6 + 10; //无向图:N*2, 反向图,N*2*2;
int n, m;
int w[N];
int hs[N], ht[N], e[M], ne[M], idx;
int dmin[N], dmax[N];
bool st[N];
void add (int h[], int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
void spfamin(int h[])
{
queue<int> q;
memset (dmin, 0x3f, sizeof (dmin));
memset(st, 0, sizeof st);
q.push(1);
dmin[1] = w[1];
st[1] = true;
while (q.size())
{
auto t = q.front();
q.pop();
st[t] = false;
for (int i=h[t]; ~i; i = ne[i])
{
int j = e[i];
if (dmin[j] > min(dmin[t], w[j]))
{
dmin[j] = min(dmin[t], w[j]);
if (!st[j])
{
st[j] = true;
q.push(j);
}
}
}
}
}
void spfamax(int h[])
{
memset (dmax, -0x3f, sizeof (dmax));
memset(st, 0, sizeof st);
queue<int> q;
q.push(n);
dmax[n] = w[n];
st[n] = true;
while (q.size())
{
auto t = q.front();
q.pop();
st[t] = false;
for (int i=h[t]; ~i; i = ne[i])
{
int j = e[i];
if (dmax[j] < max(dmax[t], w[j]))
{
dmax[j] = max(dmax[t], w[j]);
if (!st[j])
{
st[j] = true;
q.push(j);
}
}
}
}
}
int main()
{
scanf("%d%d", &n, &m);
memset(hs, -1, sizeof ht);
memset(ht, -1, sizeof ht);
for (int i=1; i <= n; i ++)
scanf("%d", &w[i]);
for (int i=1; i <= m; i ++)
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
add (hs, a, b), add (ht, b, a); //先建立一个方向的边! 单向的
if (c == 2){ //再反着建立一次。 双向的
add(hs, b, a);
add(ht, a, b);
}
}
spfamin (hs);
spfamax (ht);
int res=0;
for (int i=1; i <= n; i ++)
res = max(res, dmax[i] - dmin[i]);
printf ("%d", res);
return 0;
}
一次spfa:
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <queue>
using namespace std;
const int N = 1e5 + 10, M = 2e6 + 10; //无向图:N*2, 反向图,N*2*2;
int n, m;
int w[N];
int hs[N], ht[N], e[M], ne[M], idx;
int dmin[N], dmax[N];
bool st[N];
void add (int h[], int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
void spfa(int h[], int dist[], int type)
{
queue<int> q;
memset(st, 0, sizeof st);
if (type == 0){
memset (dist, 0x3f, sizeof (dmin));
dist[1] = w[1];
q.push(1);
st[1] = true;
}
else{
memset (dist, -0x3f, sizeof (dmax));
dist[n] = w[n];
q.push(n);
st[n] = true;
}
while (q.size())
{
auto t = q.front();
q.pop();
st[t] = false;
for (int i=h[t]; ~i; i = ne[i])
{
int j = e[i];
if (type == 0 && dist[j]>min(dist[t], w[j]) || type==1 && dist[j] < max(dist[t], w[j]))
{
if (type==0) dist[j] = min(dist[t], w[j]);
else dist[j] = max(dist[t], w[j]);
if (!st[j])
{
st[j] = true;
q.push(j);
}
}
}
}
}
int main()
{
scanf("%d%d", &n, &m);
memset(hs, -1, sizeof ht);
memset(ht, -1, sizeof ht);
for (int i=1; i <= n; i ++)
scanf("%d", &w[i]);
for (int i=1; i <= m; i ++)
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
add (hs, a, b), add (ht, b, a); //先建立一个方向的边! 单向的
if (c == 2){ //再反着建立一次。 双向的
add(hs, b, a);
add(ht, a, b);
}
}
spfa(hs, dmin, 0);
spfa(ht, dmax, 1);
int res=0;
for (int i=1; i <= n; i ++)
res = max(res, dmax[i] - dmin[i]);
cout << res << endl;
return 0;
}
dfs:
递归的思路:
- 明确目标:求的是在每个点之前买入的最小花费,每个点之后卖出的最大花费。两者作差即为最大利润!
- 所以说求解对象是每个点,每个点的最小和最大都要求出来。那么如何求了?这就与我们的枚举方式有关了!就要使得所有的情况都要枚举到,参与到最值的比较中。
- 枚举的方式是:假如现在是第 k 个点,求的是第 k 个点的之前买入的最小花费 (包含k) ,那么 在到达第 k 个点之前,有 t 个点可以一步到达 k,那么从这所有步中选出最小的那一步转移到 k,即:min( dmin(s1),dmin(s2),… dmin(st) );但是我们没有考虑的是:权值是在点上的,而不是在边上,第 k 个点上也有权值:w[k],万一 w[k] 才有最低成本价呢?所以说递推式应该是:min( dmin(s1),dmin(s2),… dmin(st),w[k] );
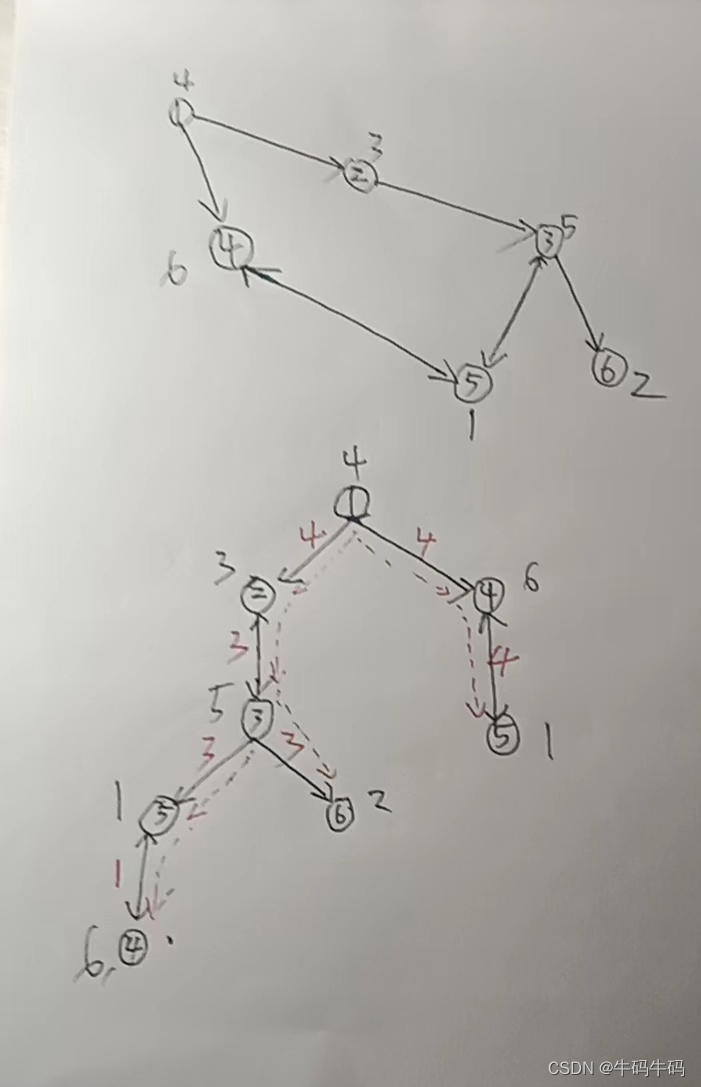
- 由于我们是一个点一个点递推的。所以说我们可以采用递归搜索来枚举每个点的最小值。求的是每个点之前买入的最小花费,即从 1~k 之间,所以说无论 k 取多少,都是从 1 号点开始,所以我们从 1 号点开始搜索如图所示:假如我要求6号点之前的最小买入的话,那么我就需要把6号点之前的点都搜索一遍,从1开始搜索。或者说直接把所有点之前的最小买入花费,都进行一遍搜索。搜索的参数:因为要更新每个点的之前买入的最小值,所以说需要不断传送最小值,与每个点的权值比较。从而使得更新完每个点的最小值。记住:递归之前的更新不叫回溯更新,递归之后才叫。这叫先更新后递归下一个点。因为图是连通图,所以一轮递归下来,每个点都会得到它之前的最小买入花费!不断将当前最小值流入每个点。
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1e5 + 10, M = 1e6 + 10;
int hs[N], ht[N], e[M], ne[M], idx;
int w[N]; //每个点的权值!
int dmin[N], dmax[N];
int n, m;
void add (int h[], int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
void dfs_min(int u, int val) //第u号点
{
if (val >= dmin[u]) return ; //表示
val = min(val, w[u]);
dmin[u] = val;
for (int i=hs[u]; ~i; i = ne[i])
{
int j = e[i];
dfs_min(j, val);
}
}
void dfs_max(int u, int val)
{
if (val <= dmax[u]) return ;
val = max(w[u], val);
dmax[u] = val;
for (int i=ht[u]; ~i; i =ne[i])
{
int j = e[i];
dfs_max (j, val);
}
}
int main()
{
scanf("%d%d", &n, &m);
memset (dmin, 0x3f, sizeof (dmin));
memset (dmax, -0x3f, sizeof (dmax));
memset(hs, -1, sizeof hs);
memset(ht, -1, sizeof ht);
for (int i=1; i <= n; i ++)
{
scanf ("%d", &w[i]);
}
for (int i=1; i <= m; i ++)
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
add(hs, a, b);
add(ht, b, a);
if (c == 2){
add (hs, b, a);
add (ht, a, b);
}
}
dfs_min(1, w[1]);
dfs_max(n, w[n]);
int res=0;
for (int i=1; i <= n; i ++)
res = max(res, dmax[i] - dmin[i]);
cout << res << endl;
return 0;
}
























 405
405











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








