[NOIP2009 提高组] Hankson的趣味题【数论易懂讲解+ 思路推敲代码 + 代码注释 + 保你看懂】

名字想不称展

已于 2023-03-16 22:16:35 修改

阅读量834

点赞数 4

分类专栏：算法刷题仓库文章标签：算法深度优先图论

于 2023-03-16 22:14:01 首次发布

本文链接：https://blog.csdn.net/m0_63613132/article/details/129577211

版权

算法刷题仓库专栏收录该内容

211 篇文章 0 订阅

订阅专栏

题目：

题目链接！

简单思路一：暴力求解–超时

如图中公式所示：我们可以利用最小公倍数为 d 来枚举所有符合要求的 x！有人说为什么不利用最大公约数呢？当然可以利用啊，但是你能列出恒等式吗？
所以说我们可以枚举d的所有约数，从而判断每个约数是否满足所有的条件即可！
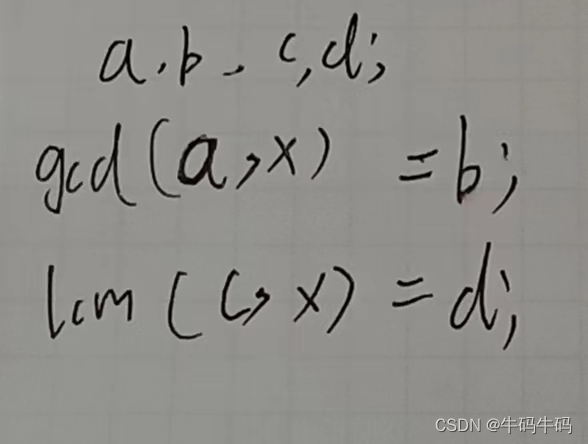
在这里插入图片描述

时间复杂度的分析上：由题目可知最多2000个数据，而每次枚举的 d 的约数，d最大值是 2*10⁹，所以如果采用 O(n^1/2)的枚举方式，其时间复杂度最多不超过 5 * 10⁴！所以说最坏情况下是：2 * 10³ * 5 * 10⁴ = 10⁸，是会超时的！
在这里插入图片描述

为什么是O(n^1/2)呢？因为存在这样的一个思想啦：一个数 x = a*b；那么必然 b = x/a；既然如此，由数学定理可得，若a <= x^1/2，则b必然大于等于 x^1/2；所以说我们只需要枚举小于等于 d^1/2的部分就好了！只有枚举某个数的因子的时候，就适合采用该做法！

下面请先看看暴力的做法：优化的思路在暴力做法的下面

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

int gcd(int a, int b)
{
    return b ? gcd(b, a%b) : a;
}

int lcm (int a, int b)
{
    return a*1ll*b/gcd(a, b);   //注意这里求最小公倍数的时候可能会爆int！
}

int main()
{
    int n;
    cin >> n;
    
    while (n --)
    {
        int a, b, c, d;
        cin >> a >> b >> c >> d;
        int cnt=0;
        //开始枚举所有的d的所有约数：
        for (int i=1; i*i <= d; i ++)
        {
            if (d%i == 0)   //前提条件：i是d的约数
            {
                if (gcd(a, i)==b && lcm(c, i)==d) //该约数满足题目所给的关系
                    cnt ++;
            
                if (i!=d/i && gcd(a, d/i)==b && lcm(c, d/i)==d)//利用因子关系判断另一个因子！
                    cnt ++;
            }    
        }
        
        cout << cnt << endl;
    }
    
    return 0;
}

优化思路：

d的约数是由：合数和质数组成的！
由算术基本定理可知:每个大于0的数都可以表示成若干个质数乘积的形式。所以说，d的约数里面每个合数都可以被质数给表示出来！
事先声明一点：d的所有约数，不是每个约数都满足题目条件的！所以说我们会枚举一些无用的约数去进行判断！
而枚举的约数的范围在5e4内，即枚举5e4次！出现的情况：总共5e4个。
1.不是约数。
2.是约数，但不满足性质。
3.是约数满足题意。
而如果我们预处理d的所有质因子呢？用质因子去求d的约数，这不就跳过了 4中的不是约数的那部分枚举了嘛！
但是枚举质因子之前得处理 1 ~ 5e4以内的所有质数！
求 [1, n] 范围内的质数的个数计算公式可得：n / ln(n)；所以可以计算得到：5e4/ln(5e4) = 5000；所以时间复杂度降低了10倍左右！再用这5000个质数去准确求出 d 的约数，判断即可！
时间复杂度为：2 * 10³ * 5 * 10³ = 1e7；

思路推敲代码：

预处理出来 d的约数范围内的所有因子：因为我们后面要去求d的所有质因子！而为了避免时间复杂度过高，我们可以先预处理出来所有的质数，然后拿质数去枚举d的所有因子，这样时间复杂度更低！

int get_primes(int n)
{
    for (int i=2; i <= n; i ++)
    {
        if (!st[i]) primes[cnt ++] = i;
        for (int j=0; primes[j]*i <= n; j ++)
        {
            st[primes[j]*i] = true;
            if (i % primes[j] == 0) break;
        }
    }
}

2.将d分解成：d = p0^c0 * p1^c1 * … * pk^ck; 存入factor[N]；枚举预处理出来的所有质数，这样的话效率更高！不用枚举不是质数的数等情况：为什么要分解d的质因子？因为我们要用d的质因子去准确的求出 d的所有约数啊！从而避免枚举不是d的约数的数！

        //对 d 进行分解：d = p0^c0 * p1^c1 * ... * pk^ck; 存入factor[N];
        cntf=0; //因为有多组测数数据，表示的是d的质因子个数
        int t = d;  //d本身不能改变，所以替代！
        for (int i=0; i < cnt; i ++)    //枚举预处理的约数个数！
        {
            int p = primes[i];
            if (t % p == 0)
            {
                int s=0;
                while (t%p == 0) s ++, t/=p;
                factor[cntf ++] = {p, s};
            }
            if (t > 1) factor[cntf ++] = {t, 1};
        }

预处理完d的所有质因子后，我们要去枚举所有质因子组成的约数，这些约数必然是可以由若干个 d的质因子的乘积的形式表达出来！可以采用递归枚举所有的组合情况：组合原因和递归树如下图所示：

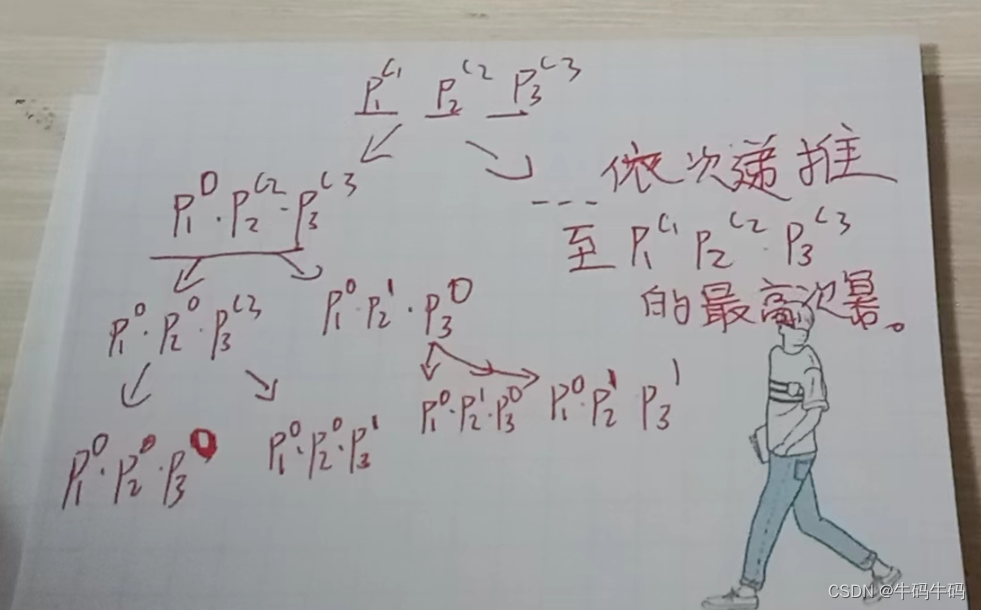
搜索的是这样的所有组合：d =  p0^c0 * p1^c1 * ... * pk^ck;
因为枚举所有幂次的组合情况,比如：
 p0^0 * p1^1 * p2^5 * ...；
 p0^2 * p1^0 * p2^7 * ...；
 只要是对应的pi的幂次小于其对应的ci，则都是d的约数！由若干质数乘积形式表达出来的约数！
void dfs (int u, int p) //u表示的是第u个质因子，p表示的是当前的值！
{
    if (u == cntf)
    {
        divider[cntd ++] = p;
        return ;
    }
    
    for (int i=0; i <= factor[u].second; i ++) //枚举p这个质因子 (0~s) 次幂的约数！
    {
        dfs(u+1, p);    //从 ^0 ^0 ^0 ... ^0 ---》^0 ^0 ^0 ... ^1；这样逐步枚举所有的组合！
        p = p*factor[u].first;  //回溯时更新分支！
    }
}

处理完求得了 d的所有约数之后，我们就去判断这些约数是否满足条件！且满足条件的约数的个数是多少？

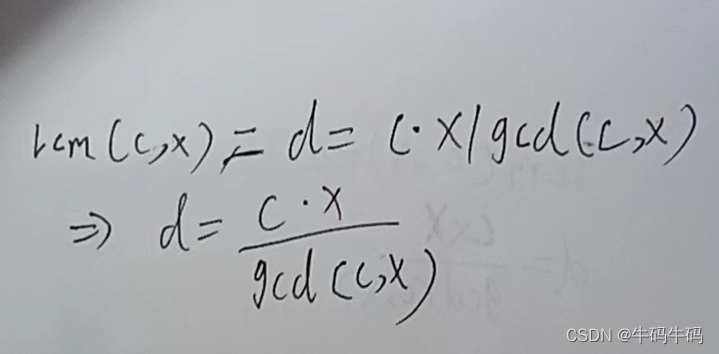
int gcd(int a, int b)
{
    return b==0?a:gcd(b, a%b);
}
int lcm(int a, int b)
{
    return a*b/gcd(a, b);
}

        int res=0;
        for (int i=0; i < cntd; i ++)
        {
            int x = divider[i];
            if (gcd(a, x) == b && (LL)c*x / gcd(c,x) == d)
            {
                res ++;
            }
        }
        
        printf ("%d\n", res);

完整代码：

#include <iostream>
#include <algorithm>
#include <vector>

using namespace std;

typedef long long LL;
typedef pair<int, int> PII;

const int N = 45000, M = 50;

int primes[N], cnt;
bool st[N];

PII factor[M];
int cntf;

int divider[N], cntd;

void get_primes(int n)
{
    for (int i = 2; i <= n; i ++ )
    {
        if (!st[i]) primes[cnt ++ ] = i;
        for (int j = 0; primes[j] <= n / i; j ++ )
        {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) break;
        }
    }
}

int gcd(int a, int b)
{
    return b ? gcd(b, a % b) : a;
}

void dfs(int u, int p)
{
    if (u > cntf)
    {
        divider[cntd ++ ] = p;
        return;
    }

    for (int i = 0; i <= factor[u].second; i ++ )
    {
        dfs(u + 1, p);
        p *= factor[u].first;
    }
}

int main()
{
    get_primes(N);

    int n;
    scanf("%d", &n);
    while (n -- )
    {
        int a0, a1, b0, b1;
        scanf("%d%d%d%d", &a0, &a1, &b0, &b1);

        int d = b1;
        cntf = 0;
        for (int i = 0; primes[i] <= d / primes[i]; i ++ )
        {
            int p = primes[i];
            if (d % p == 0)
            {
                int s = 0;
                while (d % p == 0) s ++, d /= p;
                factor[ ++ cntf] = {p, s};
            }
        }
        if (d > 1) factor[ ++ cntf] = {d, 1};

        cntd = 0;
        dfs(1, 1);

        int res = 0;
        for (int i = 0; i < cntd; i ++ )
        {
            int x = divider[i];
            if (gcd(x, a0) == a1 && (LL)x * b0 / gcd(x, b0) == b1)
            {

                res ++ ;
            }
        }

        printf("%d\n", res);
    }

    return 0;
}

含有注释：但是没有debug的代码，暂时没有找出来！

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;
const int N = 5e4+10, M = 50;//用试除法分解质因数只要枚举到根号2×10^9只要取到比这个数大即可。
int primes[N];
bool st[N];
int cnt;
typedef pair<int, int> PII;
typedef long long LL;

PII factor[M];//M表示 b1 中不同质因子的个数，这里开得比较宽松，开小一点也是可以的。
int divider[N], cntd;
int cntf;
int gcd(int a, int b)
{
    return b==0?a:gcd(b, a%b);
}
int lcm(int a, int b)
{
    return a*b/gcd(a, b);
}

int get_primes(int n)
{
    for (int i=2; i <= n; i ++)
    {
        if (!st[i]) primes[cnt ++] = i;
        for (int j=0; primes[j]*i <= n; j ++)
        {
            st[primes[j]*i] = true;
            if (i % primes[j] == 0) break;
        }
    }
}

//搜索的是这样的所有组合：d =  p0^c0 * p1^c1 * ... * pk^ck;
//因为枚举所有幂次的组合情况,比如：
// p0^0 * p1^1 * p2^5 * ...；
// p0^2 * p1^0 * p2^7 * ...；
//只要是对应的pi的幂次小于其对应的ci，则都是d的约数！由若干质数乘积形式表达出来的约数！
void dfs (int u, int p) //u表示的是第u个质因子，p表示的是当前的值！
{
    if (u == cntf)
    {
        divider[cntd ++] = p;
        return ;
    }
    
    for (int i=0; i <= factor[u].second; i ++) //枚举p这个质因子 (0~s) 次幂的约数！
    {
        dfs(u+1, p);    //从 ^0 ^0 ^0 ... ^0 ---》^0 ^0 ^0 ... ^1；这样逐步枚举所有的组合！
        p = p*factor[u].first;  //回溯时更新分支！
    }
}

int main()
{
    int n;
    cin >> n;
    get_primes(N-1);
    while (n -- )
    {
        int a, b, c, d;
        cin >> a >> b >> c >> d;
        
        //对 d 进行分解：d = p0^c0 * p1^c1 * ... * pk^ck; 存入factor[N];
        cntf=0; //因为有多组测数数据，表示的是d的质因子个数
        int t = d;  //d本身不能改变，所以替代！
        for (int i=0; i < cnt; i ++)    //枚举预处理的约数个数！
        {
            int p = primes[i];
            if (t % p == 0)
            {
                int s=0;
                while (t%p == 0) s ++, t/=p;
                factor[cntf ++] = {p, s};
            }
            if (t > 1) factor[cntf ++] = {t, 1};
        }
        
        
        cntd = 0;   //约数个数为 0；
        dfs (1, 1);
        
        int res=0;
        for (int i=0; i < cntd; i ++)
        {
            int x = divider[i];
            if (gcd(a, x) == b && (LL)c*x / gcd(c,x) == d)
            {
                res ++;
            }
        }
        
        printf ("%d\n", res);
        
    }
    
    return 0;
}