波动数列【记忆化搜索 + DP】

不求点赞，只求耐心看完，指出您的疑惑和写的不好的地方，谢谢您。本人会及时更正感谢。希望看完后能帮助您理解算法的本质

题目描述：😊

观察这个数列：
1 3 0 2 -1 1 -2 …
这个数列中后一项总是比前一项增加2或者减少3。
栋栋对这种数列很好奇，他想知道长度为 n 和为 s 而且后一项总是比前一项增加a或者减少b的整数数列可能有多少种呢？

输入格式
输入的第一行包含四个整数 n s a b，含义如前面说述。

输出格式
输出一行，包含一个整数，表示满足条件的方案数。由于这个数很大，请输出方案数除以100000007的余数。

样例输入
4 10 2 3

样例输出
2

样例说明
这两个数列分别是2 4 1 3和7 4 1 -2。

小白到进阶各种解法：😊

一、暴搜：😊😊

1. 递归的出口：因为限制了只有 $n$ 个数，等价于 $n$ 个位置，那么每个位置必须填满，所以当 $n$ 个位置都填满的时候，即为出口，但是我们还未对答案进行处理，我们还应该判断当前$n$ 个元素的和值是否等于 目标值 $s$，若等于，则方案数 + 1，反之返回0！
2. 由递归的出口可知，递归的参数，当前是第几个数了($u$)，当前的元素和是多少 $sum$，所以基于这些我们知道应该有两个参数！
3. 递归的方式：由题目可知，对于一个数而言：两个分支，一个是增量+$a$，要么是减量- $b$，所以说递归的方式如下：

dfs (u+1, x + a, sum + x+a);
dfs (u+1, x - b, sum + x-b);

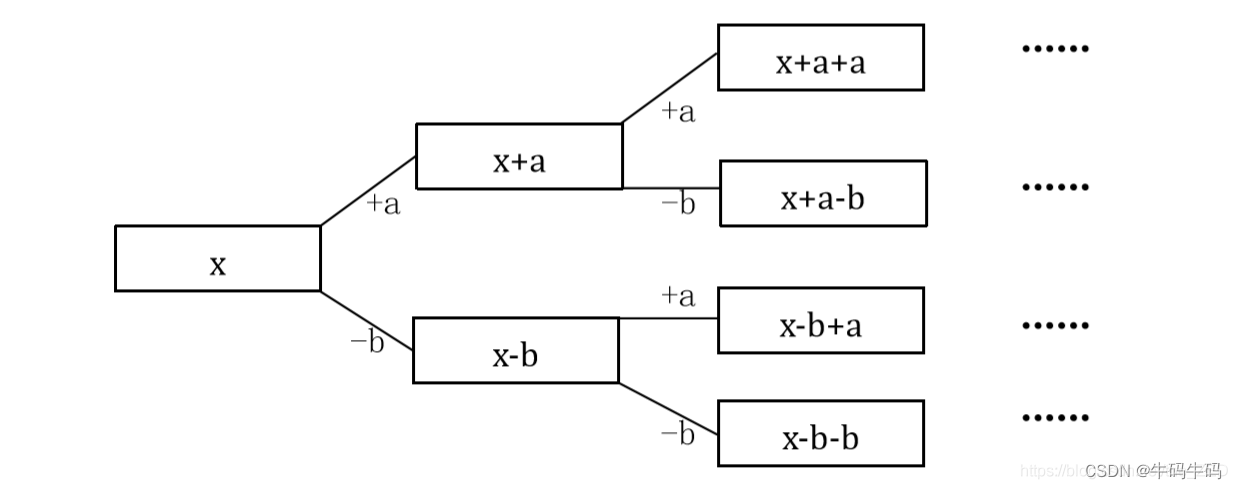
不难看出：如果正向递归的话，对于x的选取比较难入手，选不好的话，就一入递归，深似海！所以我们可以采取逆向递归！

4. 逆向递归：即从（n，s）开始递归。即从第 $n$ 个位置开始放置，往前放置，当$n$等于0的时候，说明 $n$ 个位置已经放满了，此时再判断 $s$， 将 $s$ 与当前位置上的元素和进行作差，如果差值为 0，说明当前元素和为 0，方案数+1，否则返回 0！

代码：

1. 枚举1~1e6以内的每一个数作为起点，看能否搜到答案。
2. 由于有位数的限制，即 $n$，所以说这是递归的出口！
3. 参数分析：
   x：第 u 位上的元素值，
   u：第u位数，
   ans：当前 u位的元素和！
4. 递归计算：枚举所有的组合！所有可行的分支，可见其本质还是一个组合问题！

#include<iostream> 
#include<cstring> 
using namespace std; 
int n,s,a,b; 
const int N = 1e6; 
int res; 
void dfs(int x,int u,int ans) 
{ 
    ans+=x; 
    if(u>=n) { 
        if (ans == s)
            res++; 
        return; 
    } 
    dfs(x+a,u+1,ans); 
    dfs(x-b,u+1,ans); 
    
} 
int main() 
{ 
    cin>>n>>s>>a>>b;//n是长度，s是总和，a是增加量，b是减少量 
    for(int i=0;i<N;i++)
        dfs(i,1,0);//第一个是初始值，第二个是枚举的位数 
    cout<<res; 
    return 0;
}

二、记忆化搜索：😊😊

递归的思路是：

定义一个函数 $f(i,j)$ 表示长度为 $i$ 和为 $j$ 的数列的方案数。

定义一个数组 $memo[n+1][s+1]$，其中 $memo[i][j]$ 表示 $f(i,j)$ 是否已经被计算过。

如果 $memo[i][j]$ 为真，直接返回 $f(i,j)$。

否则，根据递推公式 $f(i,j)=f(i-1,j-a)+f(i-1,j+b)$，计算出 $f(i,j)$ 并存入 $memo[i][j]$ 。

最后输出 $f(n,s)$ 。

代码：

#include <iostream>
using namespace std;

const int mod = 100000007; // 定义模数
int dp[1005][2005]; // 定义数组
bool memo[1005][2005]; // 定义备忘录

// 定义递归函数
int f(int i, int j, int a, int b) {
  // 如果已经被计算过，直接返回
  if (memo[i][j]) {
    return dp[i][j];
  }
  // 如果是边界条件，返回1或0
  if (i == 0) {
    return j == 0 ? 1 : 0;
  }
  if (i < 0 || j < -b * i) {
    return 0;
  }
  // 否则根据递推公式计算，并存入备忘录
  dp[i][j] = (f(i - 1, j - a, a, b) + f(i - 1, j + b, a ,b)) % mod;
  memo[i][j] = true;
  
 return dp[i][j];
}

int main() {
 // 输入数据
 int n, s ,a ,b;
 cin >> n >> s >> a >> b;

 // 初始化备忘录
 for (int i = 0; i <= n; i++) {
   for (int j = -b * i; j <= s + b * (n - i); j++) {
     memo[i][j] = false;
   }
 }

 // 输出结果
 cout << f(n,s,a,b) << endl;

 return 0;
}

三、本题考察算法：动态规划！😊😊

思路：

经过上述的递归分析：很明显我们可以知道这是一个组合型问题，只不过拿来组合的元素对象，并不像以往那样直接给你一个数组，让你从这n个数中选出所有满足要求的组合！

是这样吧，它是给你一个起点，让你去通过$+a$或者 $-b$ 的方式去寻找这些元素然后再枚举这些元素组合在一起的情况！

开始证明：
假设第一项是 $x$，然后变化的方式的集合：$d=[+a,-b]$ 两种方式，所以说第二项是：$x+d$；
依次类推为：
$x+(x+d_1)+(x+d_1+d_2)+(x+d_1+d_3)+...+(x+d_1+d_n)式一$
(批注：最后是$(n-1)$的下标，因为从 $x+0$ 开始的。)
然后将 式一 展开求和：
$nx+(n-1)d_1+(n-2)d_2+...+d_n-1==S式二$；
但是根据题目，只给出 $n,s,a,b$，并没有给出第一项 $x$，这意味着 $x$可能需要枚举，然而这样必定会超时，所以需要转化问题，不能直接求解，只能间接求解。

我们将 式二 进行移项，很多简单题都是移项，再利用一些数论定理从而将问题转化的；比如本题：移项后为：

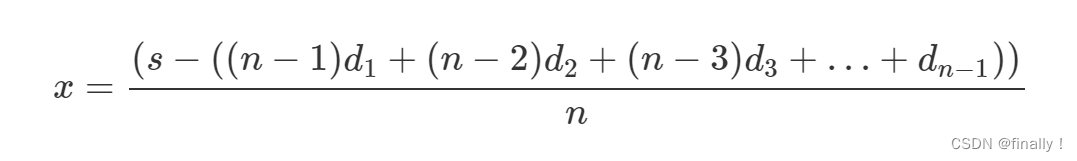
那么该等式为恒等式，由于 $x$ 是正整数，所以说右边是可以 模 n 等于0的，这意味着：我们可以将分子拆成两部分：
一部分：$A=n$
一部分：$B=(n-1)d_1+(n-2)d_2+(n-3)d_3+...+d_n-1$
可得：由商3为 $x$ 是整数可知：⇒ A%n == B%n == 0；
而我们的 $S=A$是确定的，只是序列 $d_i=B$ 不确定，
所以说问题就转化为了：我们要求出 $(n-1)d_1+(n-2)d_2+...+d_n$ 这个式子所有可能的组合模 $n$ 的余数为 s%n 的结果数！

承上启下：
由于序列$d_i$，存在许多不同的组合序列，只要 $d$这个变量变化，就意味着对应着一种新的方案，但是不一定合法，所以说我们要去求解所有合法的序列，即能否凑出满足要求的余数；

dp组合问题：
本题本质是完全背包问题；可以映射为完全背包的模板题目：从前 $i$ 种数选，所选数的总体积恰好为 $j$ 的所有选法。而这种状态的计算方式为：
$f[i][j]=f[i-1][j]+f[i-1][j-v]$

1. 状态表示：设$f[i][j]$：为选了$i$个数，前$i$个$d$的和模$n$的余数为 $j$的选法数量! 这里注意：dp是从子问题递推迭代到大问题的，直到原问题结束。所以说枚举(循环)的上限就是原问题的限制条件(稍后具体解释)，这里的 $j$不一定就是目标余数：n%s；而是从小于 n%s 的余数 $[i,j]$ 一步一步递推而来滴！
2. 明确目标：求的是：$f[n-1][s模n]$，$n-1$ 是因为没有第一项$x$；
3. 状态计算：考虑最后一个不同点，要么选 $+a$，要么$-b$。
   如果选 $+a$ 的话，前 $i$ 个数的和为：
   $[(n-1)d_1+(n-2)d_2+...+(n-(i-1))d_{i-1}+(n-i)a]\%n\equiv j\%n$
   转化为：
   $(n-1)d_1+(n-2)d_2+..+(n-(i-1))d_{i-1}\equiv j-(n-i)a$
   因为$f[i][j]$ 代表的是组合的数量，即$j-(n-i)a$是已经确定的数值(递推过的子问题)，所以变化的数量在前面已经记录了，所以直接查表可得！
   故可得：$f[i][j]=f[i-1][j-a(n-i)];$

同理，如果选 $-b$，$f[i][j]=f[i-1][j+(n-i)b]$

综上所述总的方案数为：
$f[i][j]=f[i-1][j-(n-i)a]+f[i-1][j+(n-i)b]$
但是因为第二维表示的是余数，所以需要 $[j-(...)]\%n$取余数，判断相等。而 $j-(...)$可能为负数，所以：$j\%n\Rightarrow (j\%n+n)\%n$

代码：

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1e3 + 10,  MOD = 100000007;
int f[N][N];    //f[i][j]: 表示长度为i的序列元素和，模n的余数为j的序列有多少个。
int n, s, a, b;

int get_mod(int a, int b)
{
    return (a%b + b)%b;
}

int main()
{
    cin >> n >> s >> a >> b;
    
    f[0][0] = 1;    //长度为0的序列元素和，模n为0的序列只有一种，因为元素和=0；
    for (int i=1; i <= n; i ++)
        for (int j=0; j < n; j ++)
            f[i][j] = (f[i-1][get_mod(j-(n-i)*a, n)] + f[i-1][get_mod(j+(n-i)*b, n)])%MOD;
    
    cout << f[n-1][get_mod(s, n)];
    return 0;
}