😊😊 😊😊
不求点赞,只求耐心看完,指出您的疑惑和写的不好的地方,谢谢您。本人会及时更正感谢。希望看完后能帮助您理解算法的本质
😊😊 😊😊
[NOIP2003 提高组] 加分二叉树
设一个 n n n 个节点的二叉树 tree \text{tree} tree 的中序遍历为 ( 1 , 2 , 3 , … , n ) (1,2,3,\ldots,n) (1,2,3,…,n),其中数字 1 , 2 , 3 , … , n 1,2,3,\ldots,n 1,2,3,…,n 为节点编号。每个节点都有一个分数(均为正整数),记第 i i i 个节点的分数为 d i d_i di, tree \text{tree} tree 及它的每个子树都有一个加分,任一棵子树 subtree \text{subtree} subtree(也包含 tree \text{tree} tree 本身)的加分计算方法如下:
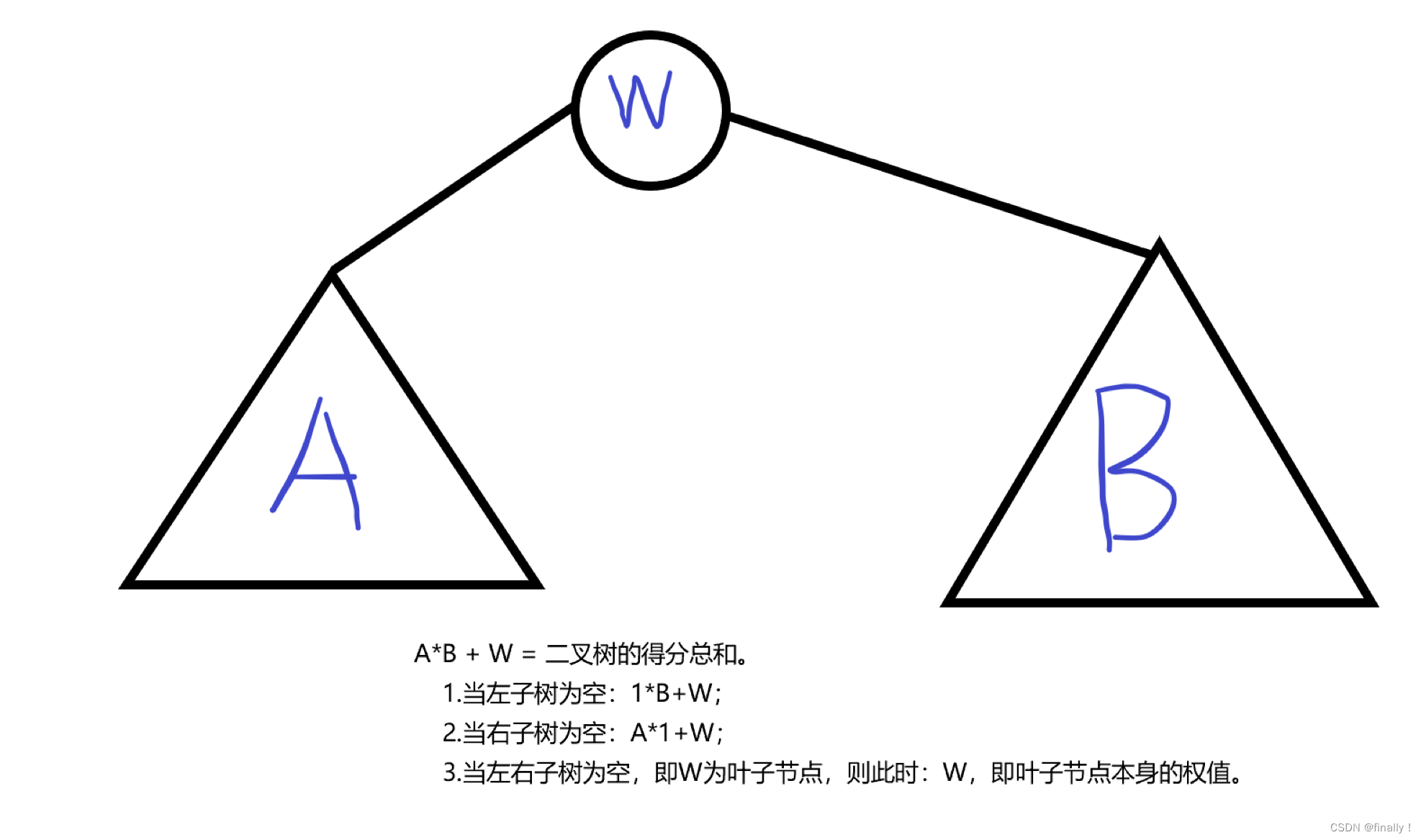
subtree \text{subtree} subtree 的左子树的加分 × \times × subtree \text{subtree} subtree 的右子树的加分 + + + subtree \text{subtree} subtree 的根的分数。
若某个子树为空,规定其加分为 1 1 1,叶子的加分就是叶节点本身的分数。不考虑它的空子树。
试求一棵符合中序遍历为 ( 1 , 2 , 3 , … , n ) (1,2,3,\ldots,n) (1,2,3,…,n) 且加分最高的二叉树 tree \text{tree} tree。要求输出
-
tree \text{tree} tree 的最高加分。
-
tree \text{tree} tree 的前序遍历。
输入格式
第 1 1 1 行 1 1 1 个整数 n n n,为节点个数。
第 2 2 2 行 n n n 个用空格隔开的整数,为每个节点的分数
输出格式
第 1 1 1 行 1 1 1 个整数,为最高加分($ Ans \le 4,000,000,000$)。
第 2 2 2 行 n n n 个用空格隔开的整数,为该树的前序遍历。
样例 #1
样例输入 #1
5
5 7 1 2 10
样例输出 #1
145
3 1 2 4 5
提示
数据规模与约定
对于全部的测试点,保证 1 ≤ n < 30 1 \leq n< 30 1≤n<30,节点的分数是小于 100 100 100 的正整数,答案不超过 4 × 1 0 9 4 \times 10^9 4×109。
一、本题考察算法:区间DP😊
思路:
分析:
D
p
Dp
Dp求解其实就是由若干个子问题的答案堆叠,从而累计到原问题的答案。每个问题的地位都是等效的,且计算公式也是一致的,只是数据规模问题而已。
由于我们是从子问题推大问题的,那么已经求解过的子问题,就不应该受到后续问题求解的影响,这叫无后效性。
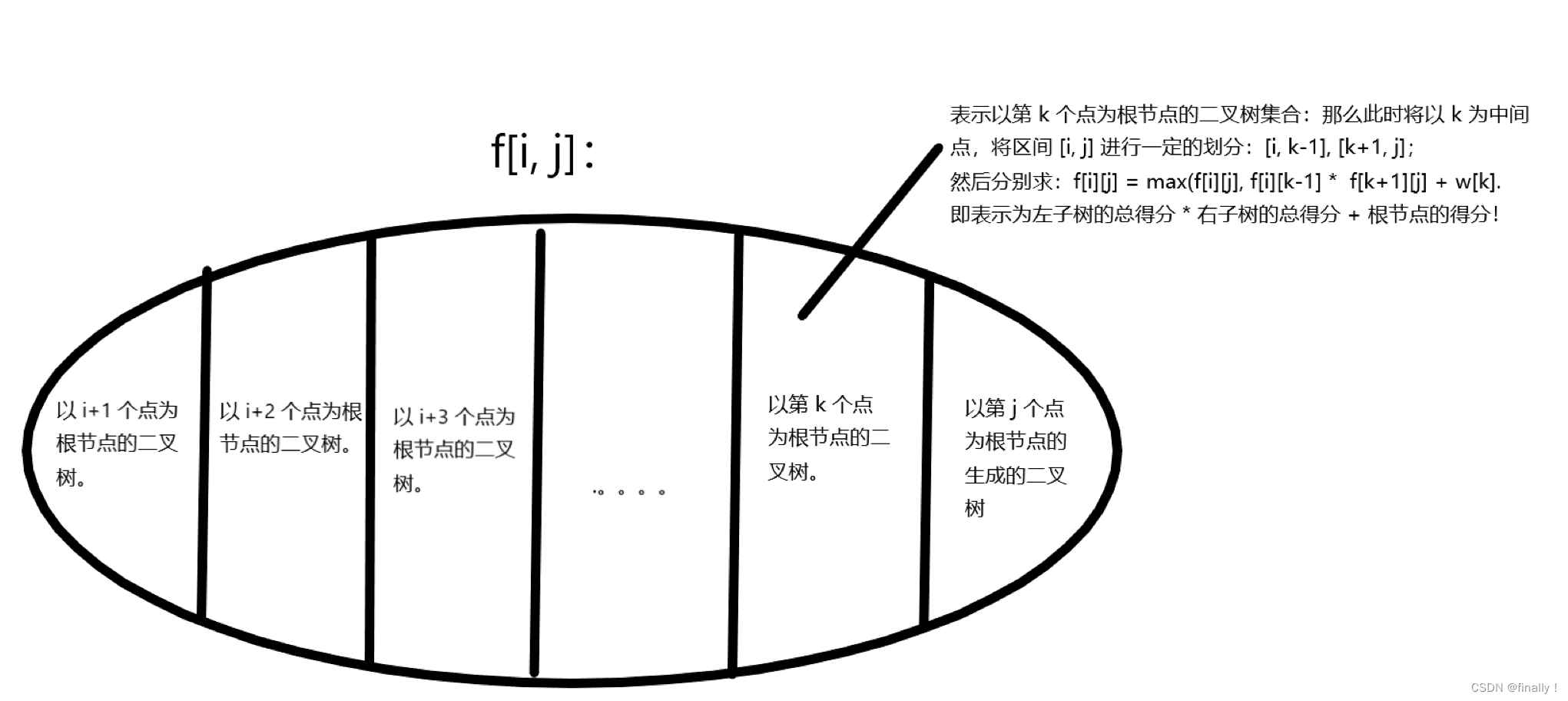
给定的中序序列,序列本质是若干个节点的集合,题目要求的是:求该中序序列所形成的树集合里,分数最高的树。那么问题的描述转化为了:求由给定的节点集合 { i . . . j i...j i...j} 所维护的树集合里,求出最大分数。
有小伙伴会问,那么怎么由这些节点集合是如何生成的树的集合呢?
注意,由于给定的是中序序列,而中序序列的性质:任选一点都可以作为某个树的根节点,该点左边的节点集合形成左子树,右边的节点集合形成右子树。从而形成一棵树。那为什么说是树的集合呢?因为中序序列中的每一个节点都可以选作根节点从而形成一棵完整的树,从而形成树的集合,但是我们并不知道哪个节点为根节点的所形成的树的分数最大。所以才需要去枚举。
如何计算呢?
所以对于节点集合 {i,… ,j} 的最大权值的树,我们可以设为:
f
[
i
]
[
j
]
:
f[i][j]:
f[i][j]:表示从节点
i
i
i 到节点
j
j
j 所形成树的最大分数。那么如何计算这个最大分数呢?由题目可知:一棵树 (子树) 的分值 = 左子树分值 * 右子树分值 + 该子树根节点的权值。由上述分析,我们可以得知左右子树区间,假设选定节点为:rt,则左子树节点集合为:
[
l
,
r
t
−
1
]
[l, rt-1]
[l,rt−1],右子树节点集合为:
[
r
t
+
1
,
r
]
[rt + 1,r]
[rt+1,r],那么此时如何计算左右子树区间的分数呢?很明显了,计算整个区间的前提是要先计算子区间,而子区间的计算又要计算它的子区间 ⇒ DP,又由于涉及区间性求解,所以可判为区间DP!
大白话证明区间DP:
区间从大划分到小,由于是树的区间,只不过不用考虑建树,给定的是中序序列。但是由于树的存在,必然会出现叶子节点,即区间长度为1的区间。又因为说了是加分二叉树,那么必然是存在长度为3的区间
[
l
e
f
t
,根节点,
r
i
g
h
t
]
[left,根节点,right]
[left,根节点,right],所以说用区间DP可以求解出不同长度区间的分数,故合法可行。
而对于每个节点区间,无论大小,我们知道二叉树的分值取决于谁是根,于是我们就在区间内枚举根节点 r o o t = k root = k root=k。即区间的分割点
思路总结:
- 给定一个二叉树的中序序列,请你求出由该中序序列所构成的二叉树集合里面,得分最大的二叉树,其得分最大是多少,并输出它的前序序列。
- 对于中序序列而言,二叉树的集合取决于根节点的决策,中序序列中的任意一个点都有可能是根节点,从而产生不同的左右子树。所以我们要求出 [i,j] 维护的二叉树里的得分最大的那棵二叉树。
- 由于根节点不同 ⇒ 二叉树不同,所以我们可以将根节点的选取,记作我们的划分依据,枚举计算
[
i
,
j
]
区间里面
[i,j]区间里面
[i,j]区间里面 每个节点生成的二叉树的得分的最大值。
- 注意事项:
推荐题解
代码:
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 35;
int w[N]; //每个节点上的分数!
int f[N][N]; //由区间[i,j]所构成的二叉树的集合!求集合中总分最大的二叉树!
int g[N][N]; //存储区间[i,j]的根节点。
int n;
void dfs(int l, int r) //根左右!
{
//l<r: 表示区间中还存在多个节点 !
//l==r:表示区间中只有一个节点 = 叶子节点!
//所以 l > r,说明节点为空,递归的出口!!
if (l > r) return ;
int k = g[l][r];
cout << k << ' '; //直接输出当前区间的根节点!
//然后递归当前区间的左子树,右子树!
dfs(l, k-1), dfs(k+1, r);
}
int main()
{
cin >> n;
for (int i=1; i <= n; i ++)
cin >> w[i];
//从小到大递推,一步一步,一边推,一边记录,顺带有时候查个表,不会回溯浪费时间
//所以效率高!
for (int len=1; len <= n; len ++)
{
for (int i=1; i+len-1 <= n; i ++) //枚举起点
{
int j = i + len - 1; //枚举有右端点
if (len == 1) //此时属于叶子节点,即区间元素只有一个!
{
f[i][j] = w[i]; //即区间分 = 节点本身的权值!
g[i][j] = i;
}
//反之就不是叶子节点!
else{
//此时区间的左右端点[i,j]已经固定了,所以说枚举[i,j]之间的划分
//方式k;比较不同的划分方式哪种划分方式带来的权值大!
for (int k=i; k <= j; k ++)
{
//左子树的分:看左子树是否为空,为空则等于1;
//只有当分割点k在左端点的时候,左子树才为空!
int l = k==i?1:f[i][k-1];
//只有当分割点在区间右端点的时候,右子树才为空!
//此时右子树的分数等于1;
int r = k==j?1:f[k+1][j];
int sum = l*r + w[k];
if (sum > f[i][j]) //如果比之前的划分方式大的话:
{
f[i][j] = sum;
//此时的划分点k,将左右子树划分为了:[i,k-1], [k+1,j]
//所以说:k是区间[i,j]的根节点!
g[i][j] = k;
}
}
}
}
}
cout << f[1][n] << endl;
//由于每个区间的根节点都存在g[i][j]里面
//而先序序列的顺序是:根,左,右。
//思考整棵树的根节点在哪个区间,其他的递归处理左右子树就行了!
//而根据我们的推导可知:最初是由[1,n]序列构造的二叉树,所以根节点
//在[1,n],又因为我们在递推求不同的根节点二叉树的分值。并且存储了最大分值。
//也记录最大分值区间的划分点:g[1][n];
dfs(1, n);
return 0;
}

记忆化搜索:一般区间DP都可以采用记忆化搜索
思路:后续更新!
代码:
#include<iostream>
#include<cstdio>
using namespace std;
int n,v[49],dp[49][49],root[49][49];
int ser(int l,int r){
if(dp[l][r]>0)return dp[l][r];
if(l==r)return v[l];
if(r<l)return 1;
for(int i=l;i<=r;i++){
int p=ser(l,i-1)*ser(i+1,r)+dp[i][i];
if(p>dp[l][r]){
dp[l][r]=p;root[l][r]=i;
}
}
return dp[l][r];
}
void print(int l,int r){
if(r<l)return;
if(l==r){printf("%d ",l);return;}
printf("%d ",root[l][r]);
print(l,root[l][r]-1);
print(root[l][r]+1,r);
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++)scanf("%d",&v[i]),dp[i][i]=v[i];
printf("%d\n",ser(1,n));
print(1,n);
return 0;
}






















 156
156











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








