😊😊 😊😊
不求点赞,只求耐心看完,指出您的疑惑和写的不好的地方,谢谢您。本人会及时更正感谢。希望看完后能帮助您理解算法的本质
😊😊 😊😊
题目描述:
一个数的序列bi,当b1 < b2 < … < bS的时候,我们称这个序列是上升的。对于给定的一个序列(a1, a2, …,aN),我们可以得到一些上升的子序列(ai1, ai2, …, aiK),这里1 <= i1 < i2 < … < iK <= N。比如,对于序列(1, 7, 3, 5, 9, 4, 8),有它的一些上升子序列,如(1, 7), (3, 4, 8)等等。这些子序列中序列和最大为18,为子序列(1, 3, 5, 9)的和. 你的任务,就是对于给定的序列,求出最大上升子序列和。注意,最长的上升子序列的和不一定是最大的,比如序列(100, 1, 2, 3)的最大上升子序列和为100,而最长上升子序列为(1, 2, 3)。
输入描述:
输入包含多组测试数据。
每组测试数据由两行组成。第一行是序列的长度N (1 <= N <= 1000)。第二行给出序列中的N个整数,这些整数的取值范围都在0到10000(可能重复)。
输出描述:
对于每组测试数据,输出其最大上升子序列和。
输入:
7
1 7 3 5 9 4 8
输出:
18
小白到进阶各种解法:
一、两重循环暴力枚举:😊
思路一:
- 枚举所有的上升子序列。
- 求出所有的上升子序列的和值。
- 从所有上升子序列中取一个和值最大的上升子序列,即为答案!
思考:怎样枚举才能做到不重不漏地枚举呢?
这里采用的是:从左往右枚举,每次枚举以第
i
i
i 个数为结尾的所有上升子序列。从而做到不重不漏枚举。因为每个数都会作为子序列的终点!
具体实现:
外层循环枚举子序列的终点,即以第
i
i
i 个数为作为当前子序列的终点,然后内层循环枚举区间
[
1
,
i
]
[1, i]
[1,i] 的上升子序列,并计算上升子序列的和。然后一个一个地取最大值即可!
代码一:
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 1e5 + 10;
long long a[N], f[N];
int main()
{
int n, res=0;
cin >> n;
for (int i=1; i <= n; i ++)
cin >> a[i];
int ans=0;
for (int i=1; i <= n; i ++)
{
int sum=0; //计算以第i个数为结尾的上升子序列的和,总之就是求出所有的上升子序列的和!
int last = 0;
for (int j=1; j <= i; j ++)
{
if (a[j] > last)
{
sum += a[j];
last = a[j];
}
}
ans = max(ans, sum);
}
cout << ans << endl;
return 0;
}
相信有同学很困惑我是如何保证序列严格单调上升的呢?
其实下面的思路二,甚至是暴搜,我都用了同样的技巧!下面思路二进行讲解更为合适!
思路二:与思路一恰好相反!
思路一的枚举方式是枚举所有以第
i
i
i 个数为结尾的上升子序列的和,思路二也可以 到不重不漏地枚举所有的上升子序列。
即外层循环子序列的起点,内层循环枚举子序列的终点 (i ~ n)。
请先看下面的代码段:代码后面有详细解释
l
a
s
t
last
last 变量!
for (int i=1; i <= n; i ++) //枚举所有子序列的起点!
{
int sum=a[i]; //记录以第i个数为起点的子序列的总和!
int last=a[i];
for (int j=i+1; j <= n; j ++)
{
if (a[j] > last) //保证子序列严格单调上升!
{
sum += a[j];
last = a[j];
}
}
ans = max(ans, sum);
}
如何保证序列严格单调上升?
关键在于我们的 l a s t last last 变量!
l a s t last last 变量的作用是:记录上升子序列的末尾的元素,既然是上升子序列的末尾元素,那么这个元素必然是整个子序列最大的值。那么每次加入一个元素就要进行迭代,迭代 l a s t last last ,想想一个元素加入到上升子序列的条件是什么,就是这个元素要大于 这个上升子序列的末尾元素啊,即大于 l a s t last last 才可以加入啊!所以说,每次加入一个新的元素,都要将 l a s t last last 变量进行迭代传递交付!!
代码二:
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 1e5 + 10;
long long a[N], f[N];
int main()
{
int n, res=0;
cin >> n;
for (int i=1; i <= n; i ++)
cin >> a[i];
int ans=0;
for (int i=1; i <= n; i ++) //枚举所有子序列的起点!
{
int sum=a[i]; //记录以第i个数为起点的子序列的总和!
int last=a[i];
for (int j=i+1; j <= n; j ++)
{
if (a[j] > last) //保证子序列严格单调上升!
{
sum += a[j];
last = a[j];
}
}
ans = max(ans, sum);
}
cout << ans << endl;
return 0;
}
二、暴搜:😊

思路1:
- 枚举序列中的每个元素,作为起点去进行搜索。
- 搜索以该点为起点的上升子序列。
- 递归的出口:当整个序列搜索完毕后,即为 u > n u>n u>n时,表示以该点为起点的序列搜索完毕!
- 递归的参数:搜索到序列中的第 u u u 个数了,当前上升子序列的和值 s u m sum sum。
- 递归计算:保证严格单调递增,就需要保证添加到序列末尾的数必须大于当前末尾元素!
for (int i=u+1; i <= n; i ++)
if(a[u] < a[i]) //先保证严格单调上升
dfs(i, sum + a[i]);
ans = max(ans, sum);
代码1:
#include<iostream>
using namespace std;
const int N = 1e5 + 10;
typedef long long LL;
int n;
int a[N];
int ans;
void dfs(int u, int sum)
{
for (int i=u+1; i <= n; i ++)
{
if(a[u] < a[i]) //先保证严格单调上升
{
dfs(i, sum + a[i]);
}
}
ans = max(ans, sum);
return;
}
int main()
{
scanf("%d", &n);
for (int i=1; i <= n; i ++)
scanf("%d", &a[i]);
for (int i=1; i <= n; i ++)
dfs(i, a[i]);
cout << ans << endl;
return 0;
}
思路2:
代码2:
#include <iostream>
#include <vector>
using namespace std;
int n, ans;
vector<int> a;
void dfs(int i, int sum) {
if (i == n) { // 达到序列末尾,更新答案
ans = max(ans, sum);
return;
}
dfs(i + 1, sum); // 不选当前元素
if (a[i] > a[i - 1]) { // 选当前元素
dfs(i + 1, sum + a[i]);
}
}
int main() {
cin >> n;
a.resize(n);
for (int i = 0; i < n; i++) {
cin >> a[i];
}
dfs(0, 0); // 从第一个元素开始搜索
cout << ans << endl;
return 0;
}

三、记忆化搜索:待更新😊

思路一:
- 记忆化数组: f [ u ] : f[u]: f[u]:表示以第u个数为起点的最大和上升子序列!
- 那么则枚举每一个元素作为上升子序列的起点。往后搜索它的上升子序列。
- 记住:
f
[
u
]
:
f[u]:
f[u]:记录的是从当前节点到末尾节点的答案,并不包含它前面的元素的情况在内!即局部答案!
代码一:
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long LL;
const int N = 1e5 + 10;
LL f[N];
int a[N];
int n;
LL dfs(int u)
{
if (f[u] != 0)
return f[u];
LL res = a[u];
for (int i=u+1; i <= n; i ++)
if (a[i] > a[u])
res = max(res, dfs(i) + a[u]);
f[u] = res;
return res;
}
int main()
{
cin >> n;
for (int i=1; i <= n; i ++)
cin >> a[i];
LL ans=0;
for (int i=1; i <= n; i ++)
ans = max(ans, dfs(i));
cout << ans;
return 0;
}
思路二:
其中,f[u]表示以第u个数为结尾的最大上升子序列和,初始化为-1,表示未被访问过。在递归中,如果f[u]已经计算过,则直接返回f[u]。否则,枚举所有比a[u]小的数a[i],递归计算以第i个数为结尾的最大上升子序列和,并更新f[u]的值。最后,枚举所有可能的结尾位置,求出所有的最大上升子序列和,并取其中最大的一个作为答案。
代码二:
#include<iostream>
#include<cstring>
using namespace std;
typedef long long LL;
const int N = 1e5 + 10;
//f[u]:表示以第u个数结尾的上升子序列的最大和值。如果该值已经计算过了,则无需再次计算.因为再次计算结果相同!
LL f[N];
LL a[N];
int n;
int dfs(int u)
{
if (f[u] != 0) //记忆化!
return f[u];
f[u] = a[u];
for (int i=1; i < u; i ++)
//a[u]表示子序列末尾的数,a[i]表示子序列内部的数!既然是以a[u]结尾,则a[u]>a[i]
if (a[u] > a[i])
//取max的原因是:从所有分支中取一个最值。因为以第u个数结尾的上升子序列存在多个分支。
//枚举取最大值!
f[u] = max(f[u], dfs(i) + a[u]);
return f[u];
}
int main()
{
cin >> n;
for (int i=1; i <= n; i ++)
cin >> a[i];
int ans=0;
for (int i=1; i <= n; i ++)
ans = max(ans, dfs(i));
cout << ans << endl;
// cout << dfs(1);
return 0;
}

四、线性DP动态规划 – O(n2)😊
思路:
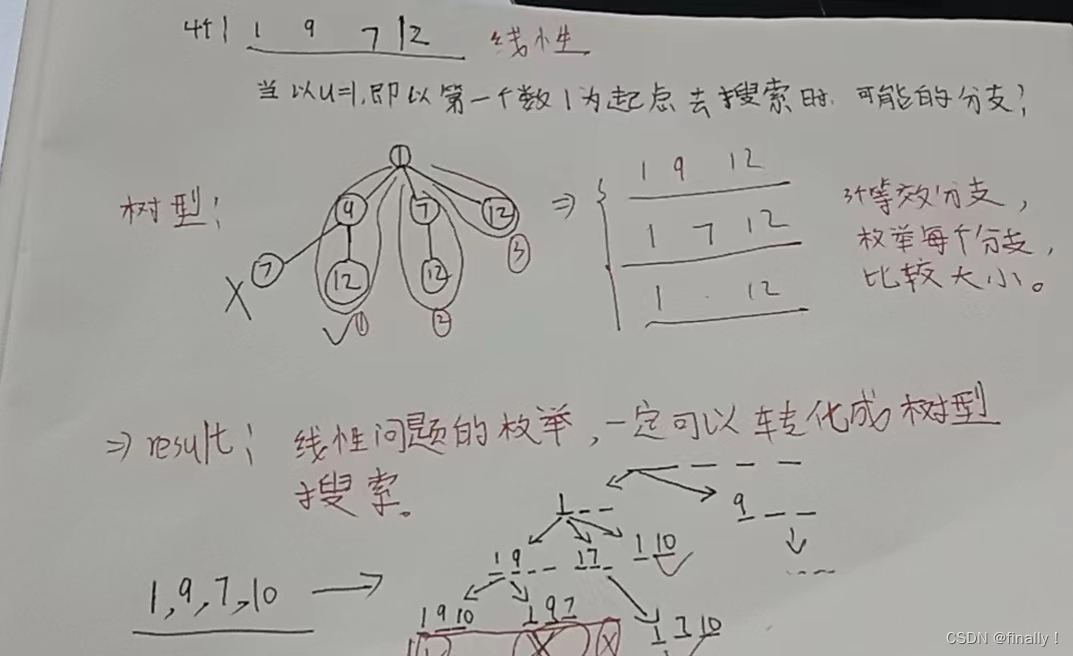
- 首先思考答案的所有子集情况:比如样例为:1, 9, 7, 10;
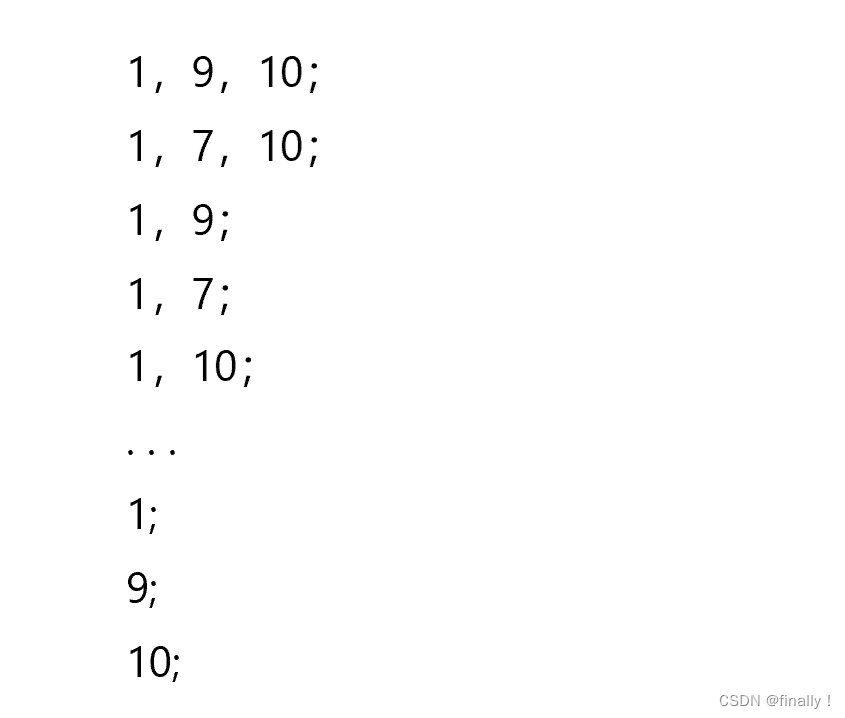
由上可知,子集数量众多,小到单独的一个数都可以作为上升子序列的和。
采用暴力循环解法的话:上面也看到了暴力循环的解法是无法AC的。
原因就是因为答案子集的数量太多,那么我们不妨将答案进行分类。保证各个类别的子集能够组合起来做到不重不漏!观察上图可知,子集可以以自己作为一个单调上升子序列,所以说为了包含这一类的话,我们不妨设 f [ u ] f[u] f[u]表示的是:以第 u u u 个数为结尾的最大上升子序列的和!从而进行划分:
比如这里以 10 结尾的子序列有:
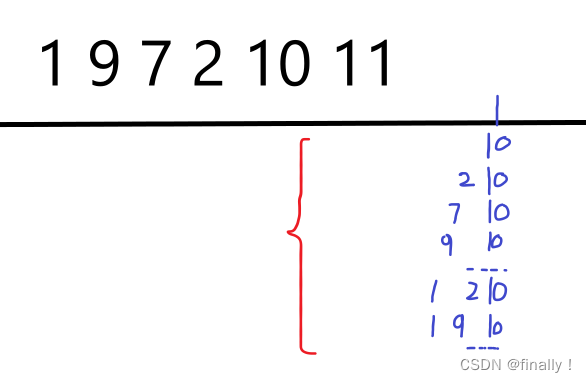
所以说以第 i i i 个数为结尾的上升子序列,我们可以将其划分为两类!包含10的子序列和不包含10的子序列。 - 如何计算每一类呢?

那我们不妨思考下,就是因为需要枚举的答案
总结:
动态规划思路:
1.状态定义:设dp[i]为以a[i]结尾的最大上升子序列和,则最终的结果就是max(dp[i]),其中0≤i<n。
2.状态转移:考虑以a[i]结尾的所有上升子序列,它们的结尾都是a[i],那么这些子序列中的最大值再加上a[i],就是以a[i]结尾的最大上升子序列和。
3.因此,对于每个i,需要枚举0到i-1的所有j,满足a[j]<a[i],然后计算dp[i]=max(dp[j])+a[i]。
4.边界条件:dp[0]=a[0]。
5.最终答案:max(dp[i])。
代码:
#include<iostream>
using namespace std;
const int N = 1e5 + 10;
int a[N];
long long f[N];
int main()
{
int n;
long long res=0;
cin >> n;
for (int i=1; i <= n; i ++)
cin >> a[i];
for (int i=1; i <= n; i ++)
{
f[i] = a[i];
for (int j=1; j < i; j ++)
{
if (a[j] < a[i])
f[i] = max(f[i], f[j] + a[i]);
}
res = max(res, f[i]);
}
cout << res << endl;
return 0;
}























 18万+
18万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








