代码随想录python笔记6 二叉树

二叉树

1. 二叉树概念

指针+左节点/右节点

种类

满二叉树:如果一棵二叉树只有度为0的结点和度为2的结点，并且度为0的结点在同一层上，则这棵二叉树为满二叉树

完全二叉树:在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2^(h-1) 个节点，堆就是一棵完全二叉树，同时保证父子节点的顺序关系

二叉搜索树:若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值。它的左、右子树也分别为二叉排序树

平衡二叉搜索树：又被称为AVL树，它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树，map、set、multimap的底层实现都是平衡二叉搜索树

---

2.二叉树的遍历

144.二叉树的前序遍历

145.二叉树的后序遍历

94.二叉树的中序遍历

以中间节点位置命名：前序遍历（中左右）中序遍历（中右左）后序遍历（左右中）

深度优先搜索：递归法、迭代法

广度优先搜索：层序遍历（迭代法）

2.1 深度优先搜索

递归法

递归三部曲：

• 确定递归函数的参数和返回值

• 确定终止条件： 操作系统用栈保存每一层递归的信息，没写终止条件或者写的不对内存栈就会溢出。

• 确定单层递归的逻辑： 确定每一层递归需要处理的信息

• 前序遍历

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def preorderTraversal(self, root: Optional[TreeNode])-> List[int]:
        res = []
        def travesal(root:TreeNode):
            if root == None:
                return
            res.append(root.val)  # 递归逻辑
            travesal(root.left)
            travesal(root.right)
        travesal(root)
        return res

• 后序遍历、中序遍历（改一下顺序就可以）

class Solution:
    def postorderTraversal(self, root: Optional[TreeNode])->List[int]:
        res = []
        def travesal(root:TreeNode):
            if root == None:
                return
            travesal(root.left)
            travesal(root.right)
            res.append(root.val)
        travesal(root)
        return res

迭代法

• 前序遍历

class Solution:
    def preorderTraversal(self, root: Optional[TreeNode])-> List[int]:
        # 迭代法--用栈模拟递归（中左右，中右左压入栈）
        res = []
        stack =[root]
        if root == None:
            return []
        while stack:
            # 加入中间节点，并弹出
            node = stack.pop()
            res.append(node.val) 
            # 加入右-左节点（出栈左-右）
            if node.right:
                stack.append(node.right)
            if node.left:
                stack.append(node.left)
        return res

• 后序遍历（与前序类似，修改左右顺序，并倒序结果）

class Solution:
    def postorderTraversal(self, root: Optional[TreeNode])->List[int]:
        # 迭代法--用栈模拟递归（左右中）->从上往下
        res = []
        stack =[root]
        if root == None:
            return []
        while stack:
            # 加入中间节点，并弹出
            node = stack.pop()
            res.append(node.val) 
            # 加入左-右节点（出栈右-左）
            if node.left:
                stack.append(node.left)
            if node.right:
                stack.append(node.right)
        return res[::-1]# (中右左-左右中)

• 中序遍历（有所不同！！）

class Solution:
    def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        # 迭代遍历（左中右）->从下往上
        if not root:
            return []
        stack = []  # 不能提前将root结点加入stack中
        result = []
        node = root
        while node or stack:
            if node:  # 如果左节点有值，先迭代访问至最底层的左子树结点   
                stack.append(cur)
                node = node.left  # 左  
            else:  # 到达最左结点后处理栈顶结点     
                node = stack.pop() # 向上迭代弹出（每次弹出最左）
                result.append(node.val)  # 中
                node = node.right    # 右
        return result

统一迭代法

中序为例：使用空指针进行标记，其他顺序只需要更改代码位置

class Solution:
    def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        # 统一迭代遍历（左中右）使用空指针作为标记
        stack = [] 
        res = []
        if root: 
            stack.append(root)
        while stack:
            node = stack.pop()
            if node:
                if node.right:
                    stack.append(node.right)
                stack.append(node)
                stack.append(None) # 标记中间节点
                if node.left:
                    stack.append(node.left)
            else:
                node = stack.pop()# 遇到空指针后，node继续迭代
                res.append(node.val)
        return res

2.2 广度优先搜索（层序遍历）

力扣题目链接

给你一个二叉树，请你返回其按 层序遍历 得到的节点值。 （即逐层地，从左到右访问所有节点）。

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：[[3],[9,20],[15,7]]

递归+层序

class Solution:
    def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
        # 递归法
        res = []
        def order(node, depth): # 确定传入参数，节点+深度
            if node == None:# 定义终止条件
                return []
            if len(res) == depth: # 初始化储存当前层结果的空列表
                res.append([])
            res[depth].append(node.val) 
            if node.left: # 递归，获取左节点的层序
                order(node.left, depth + 1)
            if node.right: # 递归，获取右节点的层序
                order(node.right, depth + 1)
        order(root, 0)
        return res

迭代+层序

class Solution:
    def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
        # 迭代法，使用队列
        if not root:
            return []
        res = []
        que = collections.deque([root])
        while que: 
            ans = []
            for i in range(len(que)): # 不断更新当前队列并且弹出
                # 按加入顺序弹出队列所有节点
                node = que.popleft()  
                ans.append(node.val) 
                # 加入下一层节点
                if node.left:
                    que.append(node.left)
                if node.right:
                    que.append(node.right)
            res.append(ans)
        return res

---

3. 翻转二叉树

力扣题目链接

翻转一棵二叉树。

示例 1：

输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]

递归+前/后序遍历

class Solution:
    def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
        # 递归实现
        if not root:
            return 
        # 前序遍历 
        root.left, root.right = root.right, root.left # 递归逻辑
        if root.left: self.invertTree(root.left)
        if root.right: self.invertTree(root.right) 
        # 后序遍历
        # if root.left: self.invertTree(root.left)
        # if root.right: self.invertTree(root.right) 
        # root.left, root.right = root.right, root.left
        # 注意，递归法+中序遍历，某些节点会被重复翻转
        return root

迭代+前/后序遍历

class Solution:
    def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
        # 迭代实现-前序遍历
        if not root:
            return 
        stack = [root]
        while stack:
            node = stack.pop()
            node.right, node.left = node.left, node.right
            if node.left:
                stack.append(node.left)
            if node.right:
                stack.append(node.right)
        return root

迭代+层序

class Solution:
    def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
        # 层序遍历-迭代实现
        que = collections.deque([root])
        while que:
            if not root:
                return 
            for i in range(len(que)):
                node = que.popleft()
                node.left, node.right = node.right, node.left
                if node.left:
                    que.append(node.left)
                if node.right:
                    que.append(node.right)
        return root

---

4. 对称二叉树

力扣题目链接

给你一个二叉树的根节点 root ， 检查它是否轴对称。

示例 1：

输入：root = [1,2,2,3,4,4,3]
输出：true

注意对称条件！

深度+递归

class Solution:
    def isSymmetric(self, root: Optional[TreeNode]) -> bool:
        def compare(left:TreeNode, right:TreeNode):# 确定传入参数，返回bool值
            # 空节点情况
            if left == None or right == None:
                if left == right:return True
                return False
            # 非空节点
            elif left.val != right.val:
                return False
            return compare(left.left, right.right) and compare(left.right, right.left) # 返回下一层递归
        if root == None: return True
        return compare(root.left, root.right)

迭代+深度

class Solution:
    def isSymmetric(self, root: Optional[TreeNode]) -> bool:
        # 使用数据结构（队列或栈）储存
        stack = []
        stack.append(root.left)
        stack.append(root.right)
        while stack:
            leftnode, rightnode = stack.pop(), stack.pop()
            if not leftnode and not rightnode: 
                continue
            if not leftnode or not rightnode or leftnode.val != rightnode.val:
                return False
            stack.append(leftnode.left)
            stack.append(rightnode.right)
            stack.append(leftnode.right)
            stack.append(rightnode.left)
        return True

迭代+层序

class Solution:
    def isSymmetric(self, root: Optional[TreeNode]) -> bool:
        # 层序遍历
        if not root:
            return True
        que = [root]
        while que:
            length = len(que)
            for i in range(length // 2):
                # 要么其中一个是None但另外一个不是
                if (not que[i] and que[length - 1 - i]) or (que[i] and not que[length - 1 - i]):
                    return False
                # 要么两个都不是None
                if que[i] and que[i].val != que[length - 1 - i].val:
                    return False
            for i in range(length):
                if not que[i]: continue
                que.append(que[i].left)
                que.append(que[i].right)
            que = que[length:]
        return True

5. 二叉树的深度

5.1. 二叉树的最大深度

力扣题目链接

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

示例： 给定二叉树 [3,9,20,null,null,15,7]，返回它的最大深度 3

递归+深度

class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        # 递归法
        if not root: return 0
        depth = max(self.maxDepth(root.left), self.maxDepth(root.right))
        return 1 + depth

迭代+层序

class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        # 迭代法
        if not root: return 0
        depth = 0 #记录深度
        queue = collections.deque([root])
        while queue:
            depth += 1
            for i in range(len(queue)):
                node = queue.popleft()
                if node.left:
                    queue.append(node.left)
                if node.right:
                    queue.append(node.right)
        return depth

5.2 n叉树的最大深度

力扣题目链接(opens new window)

给定一个 n 叉树，找到其最大深度。

最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。

例如，给定一个 3叉树 :我们应返回其最大深度，3。

递归+深度

"""
# Definition for a Node.
class Node:
    def __init__(self, val=None, children=None):
        self.val = val
        self.children = children
"""
class Solution:
    def maxDepth(self, root: 'Node') -> int:
        # 递归法
        if not root: return 0
        depth = 0
        for i in root.children:
            depth = max(depth, self.maxDepth(i))
        return depth + 1

层序+迭代-copy

class solution:
    def maxdepth(self, root: treenode) -> int:
        if not root:
            return 0
        depth = 0 #记录深度
        queue = collections.deque()
        queue.append(root)
        while queue:
            size = len(queue)
            depth += 1
            for i in range(size):
                node = queue.popleft()
                if node.left:
                    queue.append(node.left)
                if node.right:
                    queue.append(node.right)
        return depth

5.3 二叉树的最小深度

力扣题目链接

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明: 叶子节点是指没有子节点的节点。

示例:

给定二叉树 [3,9,20,null,null,15,7],返回它的最小深度 2

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。，注意是叶子节点。

什么是叶子节点，左右孩子都为空的节点才是叶子节点

递归+深度

• 确定递归函数的参数和返回值：传入节点，返回叶子节点深度

• 确定终止条件 ：遇到空节点

• 确定单层递归的逻辑：

  • 如果左子树为空，右子树不为空，最小深度是 1 + 右子树的深度。
  • 如果右子树为空，左子树不为空，最小深度是 1 + 左子树的深度。
  • 如果左右子树都不为空，返回左右子树深度最小值 + 1

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def minDepth(self, root: Optional[TreeNode]) -> int:
        # def getdepth(node):
        if root == None: return 0  # 终止条件
        leftdepth = self.minDepth(root.left)
        rightdepth = self.minDepth(root.right)
        if root.left == None and root.right != None: # 左为空，右不为空
            return 1 + rightdepth
        if root.right == None and root.left:  # 左不为空，右为空
            return 1 + leftdepth
        return 1 + min(leftdepth, rightdepth) # 都为空

迭代+层序

# 层序遍历
class Solution:
    def minDepth(self, root: TreeNode) -> int:
        if not root:
            return 0
        que = deque()
        que.append(root)
        res = 1
        while que:
            for _ in range(len(que)):
                node = que.popleft()
                # 当左右孩子都为空的时候，说明是最低点的一层了，退出
                if not node.left and not node.right:
                    return res
                # 加入下一层
                if node.left:
                    que.append(node.left)
                if node.right:
                    que.append(node.right)
            res += 1 # 记录层数
        return res

6. 完全二叉树

力扣题目链接

给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。

完全二叉树 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。

示例 1：

输入：root = [1,2,3,4,5,6] 输出：6

6.1 普通二叉树方法

深度+递归

• 时间复杂度：O(n)
• 空间复杂度：O(log n)，算上了递归系统栈占用的空间

class Solution:
    def countNodes(self, root: Optional[TreeNode]) -> int:
        # 普通二叉树方法-递归
        if root == None: return 0
        return 1 + (self.countNodes(root.right) + self.countNodes(root.left))

层序+迭代

• 时间复杂度：O(n)
• 空间复杂度：O(n)

class Solution:
    def countNodes(self, root: Optional[TreeNode]) -> int:
        # 层序+迭代
        if root == None:
            return 0
        que = collections.deque([root])
        result = 0
        while que:
            for _ in range(len(que)):
                node = que.popleft()
                if node.left:
                    que.append(node.left)
                if node.right:
                    que.append(node.right)
                result += 1
        return result

6.2 完全二叉树

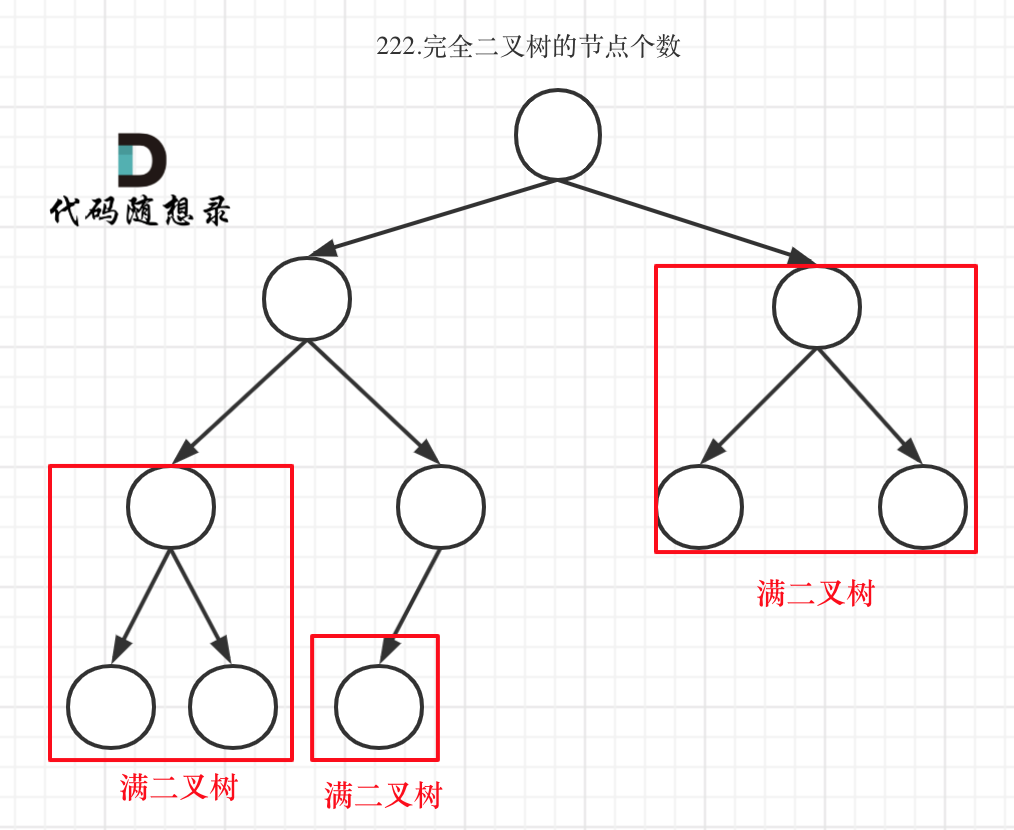
完全二叉树只有两种情况，情况一：就是满二叉树，情况二：最后一层叶子节点没有满。

对于情况一，可以直接用 2^树深度 - 1 来计算，注意这里根节点深度为1。

对于情况二，分别递归左孩子，和右孩子，递归到某一深度一定会有左孩子或者右孩子为满二叉树，然后依然可以按照情况1来计算

如果递归向左遍历的深度等于递归向右遍历的深度，那说明就是满二叉树

递归三部曲：

• 确定递归函数的参数和返回值：传入节点

• 确定终止条件： 遇到空节点停止迭代

• 确定单层递归的逻辑： 判断是否为满二叉树，并记录深度。遇到满二叉树，返回满二叉树节点数为2^树深度 - 1

• 时间复杂度：O(log n × log n)

• 空间复杂度：O(log n）

class Solution:
    def countNodes(self, root: TreeNode) -> int:
        if not root:
            return 0
        left = root.left
        right = root.right
        leftDepth = 0 #这里初始为0是有目的的，为了下面求指数方便
        rightDepth = 0
        # 判断是否为满二叉树
        while left: #求左子树深度
            left = left.left
            leftDepth += 1
        while right: #求右子树深度
            right = right.right
            rightDepth += 1
        if leftDepth == rightDepth: # 递归终止条件
            return (2 << leftDepth) - 1 # 注意位运算(2<<1) 相当于2^2，所以leftDepth初始为0
        return self.countNodes(root.left) + self.countNodes(root.right) + 1 # 递归至满二叉树

7. 平衡二叉树

力扣题目链接(opens new window)

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1。

示例 1:

给定二叉树 [3,9,20,null,null,15,7]

返回 true 。

示例 2:

给定二叉树 [1,2,2,3,3,null,null,4,4]

返回 false 。

递归+后序

递归三部曲：

• 确定递归函数的参数和返回值：传入节点

• 确定终止条件： 遇到空节点

• 确定单层递归的逻辑： 记录高度。判断是否平衡二叉树，如果不是返回-1，如果是，返回高度

class Solution:
    def isBalanced(self, root: Optional[TreeNode]) -> bool:
        def getHeight(node): 
            if node == None: # 确定终止条件
                return 0
            rh, lh = getHeight(node.right),getHeight(node.left)
            if rh == -1 or lh == -1 or abs(rh-lh) > 1:  # 判断是否平衡二叉树，如果不是返回-1
                return -1
            return 1 + max(rh, lh) # 如果是，返回高度
        return True if getHeight(root) != -1 else False

迭代+后序-copy

先定义一个函数，专门用来求高度。

这个函数通过栈模拟的后序遍历找每一个节点的高度（其实是通过求传入节点为根节点的最大深度来求的高度）

class Solution:
    def isBalanced(self, root: Optional[TreeNode]) -> bool:
        if not root:
            return True

        height_map = {}
        stack = [root]
        while stack:
            node = stack.pop()
            if node:
                stack.append(node)
                stack.append(None)
                if node.left: stack.append(node.left)
                if node.right: stack.append(node.right)
            else:
                real_node = stack.pop()
                left, right = height_map.get(real_node.left, 0), height_map.get(real_node.right, 0)
                if abs(left - right) > 1:
                    return False
                height_map[real_node] = 1 + max(left, right)
        return True

8. 二叉树的所有路径

力扣题目链接(opens new window)

给定一个二叉树，返回所有从根节点到叶子节点的路径。

说明: 叶子节点是指没有子节点的节点。

示例:

递归也需要用回溯

递归

我们先使用递归的方式，来做前序遍历。要知道递归和回溯就是一家的，本题也需要回溯

class Solution:
    def binaryTreePaths(self, root: Optional[TreeNode]) -> List[str]:
        if root == None:
            return []
        path = []
        res = []
        def travesal(node,path,res):
            path.append(node.val)
            if node.right == None and node.left == None:
                strings = str(path[0])
                for i in range(1,len(path)):
                    strings = strings + "->" + str(path[i] )
                res.append(strings)
            if node.right:
                travesal(node.right,path,res)
                path.pop() # 回溯
            if node.left:
                travesal(node.left,path,res)
                path.pop()
        travesal(root,path,res)
        return res

class Solution:
    def binaryTreePaths(self, root: Optional[TreeNode]) -> List[str]:
        if root == None:
            return []
        path = ""
        res = []
        def travesal(node,path,res):
            path += str(node.val)
            if node.right == None and node.left == None:
                res.append(path)
            if node.right:
                travesal(node.right,path + "->",res) # 隐藏回溯
            if node.left:
                travesal(node.left,path + "->",res)
        travesal(root,path,res)
        return res

迭代法

class Solution:
    def binaryTreePaths(self, root: Optional[TreeNode]) -> List[str]:
        # 迭代法
        from collections import deque
        nodes, paths, res = [root], [str(root.val)], []
        while nodes:
            node = nodes.pop()
            path = paths.pop()
            if not node.left and not node.right:
                res.append(path)
            if node.left:
                nodes.append(node.left)
                paths.append(path + "->" + str(node.left.val))
            if node.right:
                nodes.append(node.right)
                paths.append(path +"->" + str(node.right.val))
        return res

9. 左叶子之和

力扣题目链接(opens new window)

计算给定二叉树的所有左叶子之和。

示例：

递归法

class Solution:
    def sumOfLeftLeaves(self, root: Optional[TreeNode]) -> int:
        if root == None:return 0
        leftvalue = 0
        if root.left != None and root.left.left == None and root.left.right == None:
            leftvalue = root.left.val
        return leftvalue + self.sumOfLeftLeaves(root.left) + self.sumOfLeftLeaves(root.right)

迭代-copy

class Solution:
    def sumOfLeftLeaves(self, root: TreeNode) -> int:
        """
        Idea: Each time check current node's left node. 
              If current node don't have one, skip it. 
        """
        stack = []
        if root: 
            stack.append(root)
        res = 0
        
        while stack: 
            # 每次都把当前节点的左节点加进去. 
            cur_node = stack.pop()
            if cur_node.left and not cur_node.left.left and not cur_node.left.right: 
                res += cur_node.left.val
                
            if cur_node.left: 
                stack.append(cur_node.left)
            if cur_node.right: 
                stack.append(cur_node.right)
                
        return res

10. 找树左下角的值

力扣题目链接(opens new window)

给定一个二叉树，在树的最后一行找到最左边的值。

示例 1:

示例 2:

层序遍历

取最后一层的第一个节点

class Solution:
    def findBottomLeftValue(self, root: Optional[TreeNode]) -> int:
        # 层序遍历，记录最左下的值
        if root == None :return 
        que = collections.deque([root])
        while que:
            for i in range(len(que)):
                node = que.popleft() # 不断覆盖上一层，最后为最后一层的第一个节点（左）
                if i == 0: res = node.val
                if node.left: que.append(node.left)
                if node.right: que.append(node.right)
        return res

递归+回溯-copy

class Solution:
    def findBottomLeftValue(self, root: TreeNode) -> int:
        max_depth = -float("INF")
        leftmost_val = 0

        def __traverse(root, cur_depth): 
            nonlocal max_depth, leftmost_val
            if not root.left and not root.right: 
                if cur_depth > max_depth: 
                    max_depth = cur_depth
                    leftmost_val = root.val  
            if root.left: 
                cur_depth += 1
                __traverse(root.left, cur_depth)
                cur_depth -= 1
            if root.right: 
                cur_depth += 1
                __traverse(root.right, cur_depth)
                cur_depth -= 1

        __traverse(root, 0)
        return leftmost_val

11. 路径总和

力扣题目链接(opens new window)

给定一个二叉树和一个目标和，判断该树中是否存在根节点到叶子节点的路径，这条路径上所有节点值相加等于目标和。

说明: 叶子节点是指没有子节点的节点。

示例:  给定如下二叉树，以及目标和 sum = 22，

返回 true, 因为存在目标和为 22 的根节点到叶子节点的路径 5->4->11->2。

详细递归回溯

class Solution:
    def hasPathSum(self, root: Optional[TreeNode], targetSum: int) -> bool:
        
        def traversal(node,count):
            if node.left == None and node.right == None:
                if count == 0:return True
                else:return False
            if node.left:
                count -= node.left.val
                if traversal(node.left, count):return True
                count +=  node.left.val
            if node.right:
                count -= node.right.val
                if traversal(node.right, count):return True
                count +=  node.right.val
            return False
        if root == None:return False
        targetSum -= root.val
        return traversal(root,targetSum)
        

简化递归

class Solution:
    def hasPathSum(self, root: Optional[TreeNode], targetSum: int) -> bool:
        if root == None: return False
        targetSum -= root.val
        if root.right == None and root.left == None:
            if targetSum == 0: return True
        return self.hasPathSum(root.right, targetSum) or self.hasPathSum(root.left, targetSum)

迭代-层序-copy

class solution:
    def haspathsum(self, root: treenode, targetsum: int) -> bool:
        if not root: 
            return false

        stack = []  # [(当前节点，路径数值), ...]
        stack.append((root, root.val))
        while stack: 
            cur_node, path_sum = stack.pop()
            if not cur_node.left and not cur_node.right and path_sum == targetsum: 
                return true
            if cur_node.right: 
                stack.append((cur_node.right, path_sum + cur_node.right.val))    
            if cur_node.left: 
                stack.append((cur_node.left, path_sum + cur_node.left.val))

        return false

12. 从中序与后序遍历序列构造二叉树

力扣题目链接(opens new window)

根据一棵树的中序遍历与后序遍历构造二叉树。

注意: 你可以假设树中没有重复的元素。

例如，给出

中序遍历 inorder = [9,3,15,20,7] 后序遍历 postorder = [9,15,7,20,3] 返回如下的二叉树：

递归

class Solution:
    def buildTree(self, inorder: List[int], postorder: List[int]) -> Optional[TreeNode]:
        if not postorder: return None
        # 找到后序最后一个作为中间节点，切割中序
        root_val = postorder[-1]
        root = TreeNode(root_val)
        idx = inorder.index(root_val)
        inorder_left = inorder[ : idx] # 左闭右开
        inorder_right = inorder[idx + 1 : ]
        # 后序子树 = 中序子树
        postorder_left = postorder[:len(inorder_left)]
        postorder_right = postorder[len(inorder_left):len(postorder)-1]
        # 递归
        root.left = self.buildTree(inorder_left,postorder_left) 
        root.right = self.buildTree(inorder_right,postorder_right) 
        return root

前序+中序

class Solution:
    def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:
        if not preorder: return None
        # 找到后序最后一个作为中间节点，切割中序
        root_val = preorder[0]
        root = TreeNode(root_val)
        idx = inorder.index(root_val)
        inorder_left = inorder[ : idx] # 左闭右开
        inorder_right = inorder[idx + 1 : ]
        # 前序子树 = 中序子树
        preorder_left = preorder[1:1+len(inorder_left)]
        preorder_right = preorder[1+len(inorder_left):]
        # 递归
        root.left = self.buildTree(preorder_left,inorder_left) 
        root.right = self.buildTree(preorder_right,inorder_right) 
        return root

13.最大二叉树

力扣题目地址(opens new window)

给定一个不含重复元素的整数数组。一个以此数组构建的最大二叉树定义如下：

• 二叉树的根是数组中的最大元素。
• 左子树是通过数组中最大值左边部分构造出的最大二叉树。
• 右子树是通过数组中最大值右边部分构造出的最大二叉树。

通过给定的数组构建最大二叉树，并且输出这个树的根节点。

示例 ：

提示：

给定的数组的大小在 [1, 1000] 之间。

递归

class Solution:
    def constructMaximumBinaryTree(self, nums: List[int]) -> Optional[TreeNode]:
        if not nums: return None 
        root = TreeNode(max(nums))
        idx = nums.index(max(nums))
        leftnums, rightnums = nums[:idx], nums[idx+1:]
        root.left = self.constructMaximumBinaryTree(leftnums)
        root.right = self.constructMaximumBinaryTree(rightnums)
        return root

14. 合并二叉树

力扣题目链接(opens new window)

给定两个二叉树，想象当你将它们中的一个覆盖到另一个上时，两个二叉树的一些节点便会重叠。

你需要将他们合并为一个新的二叉树。合并的规则是如果两个节点重叠，那么将他们的值相加作为节点合并后的新值，否则不为 NULL 的节点将直接作为新二叉树的节点。

示例 1:

注意: 合并必须从两个树的根节点开始。

递归法

class Solution:
    def mergeTrees(self, root1: Optional[TreeNode], root2: Optional[TreeNode]) -> Optional[TreeNode]:
        # 递归法
        if not root1:return root2
        if not root2:return root1
        # 直接在原有树上修改
        root1.val += root2.val
        root1.left, root1.right = self.mergeTrees(root1.left,root2.left),self.mergeTrees(root1.right, root2.right)
        return root1

迭代法-copy

class Solution:
    def mergeTrees(self, root1: TreeNode, root2: TreeNode) -> TreeNode:
        if not root1: 
            return root2
        if not root2: 
            return root1

        queue = deque()
        queue.append(root1)
        queue.append(root2)

        while queue: 
            node1 = queue.popleft()
            node2 = queue.popleft()
            # 更新queue
            # 只有两个节点都有左节点时, 再往queue里面放.
            if node1.left and node2.left: 
                queue.append(node1.left)
                queue.append(node2.left)
            # 只有两个节点都有右节点时, 再往queue里面放.
            if node1.right and node2.right: 
                queue.append(node1.right)
                queue.append(node2.right)

            # 更新当前节点. 同时改变当前节点的左右孩子. 
            node1.val += node2.val
            if not node1.left and node2.left: 
                node1.left = node2.left
            if not node1.right and node2.right: 
                node1.right = node2.right

        return root1

15. 二叉搜索树中的搜索

力扣题目地址(opens new window)

给定二叉搜索树（BST）的根节点和一个值。 你需要在BST中找到节点值等于给定值的节点。 返回以该节点为根的子树。 如果节点不存在，则返回 NULL。

例如，

在上述示例中，如果要找的值是 5，但因为没有节点值为 5，我们应该返回 NULL

递归法

class Solution:
    def searchBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:
        if root == None or root.val == val:
            return root 
        if root.val > val:
            return self.searchBST(root.left, val)
        if root.val < val:
            return self.searchBST(root.right, val)

迭代法

class Solution:
    def searchBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:
        while root:
            if root.val > val: root = root.left
            elif root.val < val: root = root.right
            else: return root
        return None

16. 验证二叉搜索树

力扣题目链接(opens new window)

给定一个二叉树，判断其是否是一个有效的二叉搜索树。

假设一个二叉搜索树具有如下特征：

• 节点的左子树只包含小于当前节点的数。
• 节点的右子树只包含大于当前节点的数。
• 所有左子树和右子树自身必须也是二叉搜索树。

递归-压缩为数组，判断是否递增

class Solution:
    def isValidBST(self, root: Optional[TreeNode]) -> bool:
        # 中序遍历后，得到的数组应该是递增的
        res = []
        def travesal(node):
            if node == None: return None
            travesal(node.left)
            res.append(node.val)
            travesal(node.right)
        travesal(root)
        for i in range(len(res) - 1):
            if res[i] >= res[i+1]:
                return False
        return True

递归-copy

class Solution:
    def isValidBST(self, root: TreeNode) -> bool:
        cur_max = -float("INF")
        def __isValidBST(root: TreeNode) -> bool: 
            nonlocal cur_max
            if not root: 
                return True
            is_left_valid = __isValidBST(root.left)
            if cur_max < root.val: 
                cur_max = root.val
            else: 
                return False
            is_right_valid = __isValidBST(root.right)
            
            return is_left_valid and is_right_valid
        return __isValidBST(root)

迭代 - copy

迭代-中序遍历
class Solution:
    def isValidBST(self, root: TreeNode) -> bool:
        stack = []
        cur = root
        pre = None
        while cur or stack:
            if cur: # 指针来访问节点，访问到最底层
                stack.append(cur)
                cur = cur.left
            else: # 逐一处理节点
                cur = stack.pop()
                if pre and cur.val <= pre.val: # 比较当前节点和前节点的值的大小
                    return False
                pre = cur 
                cur = cur.right
        return True

17. 二叉搜索树的最小绝对差

力扣题目链接(opens new window)

给你一棵所有节点为非负值的二叉搜索树，请你计算树中任意两节点的差的绝对值的最小值。

示例：

提示：树中至少有 2 个节点

递归-化为有序数组

class Solution:
    def getMinimumDifference(self, root: TreeNode) -> int:
        res = []   
        r = float("inf")
        def buildaList(root):  //把二叉搜索树转换成有序数组
            if not root: return None
            if root.left: buildaList(root.left)  //左
            res.append(root.val)  //中
            if root.right: buildaList(root.right)  //右
            return res
            
        buildaList(root)
        for i in range(len(res)-1):  // 统计有序数组的最小差值
            r = min(abs(res[i]-res[i+1]),r)
        return r

递归-递归过程直接计算

class Solution:
    def getMinimumDifference(self, root: Optional[TreeNode]) -> int:  
        # 法2 直接在递归逻辑中实现
        pre = None
        ans = float('inf')
        def travesal(node):
            nonlocal pre
            nonlocal ans
            if node == None: return None
            travesal(node.left)
            if pre != None:
                ans = min(abs(node.val - pre.val), ans)
            pre = node
            travesal(node.right)
        travesal(root)
        return ans

迭代 - copy

class Solution:
    def getMinimumDifference(self, root: TreeNode) -> int:
        stack = []
        cur = root
        pre = None
        result = float('inf')
        while cur or stack:
            if cur: # 指针来访问节点，访问到最底层
                stack.append(cur)
                cur = cur.left
            else: # 逐一处理节点
                cur = stack.pop()
                if pre: # 当前节点和前节点的值的差值
                    result = min(result, abs(cur.val - pre.val))
                pre = cur
                cur = cur.right
        return result

18. 二叉搜索树中的众数

力扣题目链接(opens new window)

给定一个有相同值的二叉搜索树（BST），找出 BST 中的所有众数（出现频率最高的元素）。

假定 BST 有如下定义：

• 结点左子树中所含结点的值小于等于当前结点的值
• 结点右子树中所含结点的值大于等于当前结点的值
• 左子树和右子树都是二叉搜索树

例如：

给定 BST [1,null,2,2],

返回[2].

提示：如果众数超过1个，不需考虑输出顺序

进阶：你可以不使用额外的空间吗？（假设由递归产生的隐式调用栈的开销不被计算在内

不考虑二叉搜索特性

递归法

class Solution:
    def __init__(self):
        self.pre = TreeNode()
        self.count = 0
        self.maxcount = 0
        self.res = []
    def searchMode(self, cur):
        if cur == None: return
        self.searchMode(cur.left)
        if self.pre == None:
            self.count = 1
        elif self.pre.val == cur.val:
            self.count += 1
        else:
            self.count = 1
        if self.count == self.maxcount:
            self.res.append(cur.val)
        if self.count > self.maxcount:
            self.res = [cur.val]
        self.pre = cur
        self.maxcount = max(self.count, self.maxcount)
        self.searchMode(cur.right)

    def findMode(self, root: Optional[TreeNode]) -> List[int]:
        # 直接在递归中实现查找
        self.searchMode(root)
        return self.res

19. 二叉树的最近公共祖先—

力扣题目链接(opens new window)

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉树:  root = [3,5,1,6,2,0,8,null,null,7,4]

示例 1: 输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1 输出: 3 解释: 节点 5 和节点 1 的最近公共祖先是节点 3。

示例 2: 输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4 输出: 5 解释: 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。

说明:

• 所有节点的值都是唯一的。
• p、q 为不同节点且均存在于给定的二叉树中

二叉搜索树的最近公共祖先

力扣题目链接(opens new window)

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

示例 1:

• 输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
• 输出: 6
• 解释: 节点 2 和节点 8 的最近公共祖先是 6。

示例 2:

• 输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
• 输出: 2
• 解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。

说明:

• 所有节点的值都是唯一的。
• p、q 为不同节点且均存在于给定的二叉搜索树中。

二叉搜索树中的插入操作

力扣题目链接(opens new window)

给定二叉搜索树（BST）的根节点和要插入树中的值，将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据保证，新值和原始二叉搜索树中的任意节点值都不同。

注意，可能存在多种有效的插入方式，只要树在插入后仍保持为二叉搜索树即可。 你可以返回任意有效的结果。

提示：

• 给定的树上的节点数介于 0 和 10^4 之间
• 每个节点都有一个唯一整数值，取值范围从 0 到 10^8
• -10^8 <= val <= 10^8
• 新值和原始二叉搜索树中的任意节点值都不同

删除二叉搜索树中的节点

力扣题目链接(opens new window)

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

一般来说，删除节点可分为两个步骤：

首先找到需要删除的节点； 如果找到了，删除它。 说明： 要求算法时间复杂度为 $O(h)$，h 为树的高度。

示例:

修剪二叉搜索树

力扣题目链接(opens new window)

给定一个二叉搜索树，同时给定最小边界L 和最大边界 R。通过修剪二叉搜索树，使得所有节点的值在[L, R]中 (R>=L) 。你可能需要改变树的根节点，所以结果应当返回修剪好的二叉搜索树的新的根节点。

将有序数组转换为二叉搜索树

力扣题目链接(opens new window)

将一个按照升序排列的有序数组，转换为一棵高度平衡二叉搜索树。

本题中，一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1。

示例:

把二叉搜索树转换为累加树

力扣题目链接(opens new window)

给出二叉 搜索 树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。

提醒一下，二叉搜索树满足下列约束条件：

节点的左子树仅包含键 小于 节点键的节点。 节点的右子树仅包含键 大于 节点键的节点。 左右子树也必须是二叉搜索树。

示例 1：

• 输入：[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
• 输出：[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]

总结

二叉树的遍历方式

• 深度优先遍历
  • 二叉树：前中后序递归法 (opens new window)：递归三部曲初次亮相
  • 二叉树：前中后序迭代法（一） (opens new window)：通过栈模拟递归
  • 二叉树：前中后序迭代法（二）统一风格(opens new window)
• 广度优先遍历
  • 二叉树的层序遍历 (opens new window)：通过队列模拟

二叉树的属性

• 二叉树：是否对称
  • 递归：后序，比较的是根节点的左子树与右子树是不是相互翻转
  • 迭代：使用队列/栈将两个节点顺序放入容器中进行比较
• 二叉树：求最大深度
  • 递归：后序，求根节点最大高度就是最大深度，通过递归函数的返回值做计算树的高度
  • 迭代：层序遍历
• 二叉树：求最小深度
  • 递归：后序，求根节点最小高度就是最小深度，注意最小深度的定义
  • 迭代：层序遍历
• 二叉树：求有多少个节点
  • 递归：后序，通过递归函数的返回值计算节点数量
  • 迭代：层序遍历
• 二叉树：是否平衡
  • 递归：后序，注意后序求高度和前序求深度，递归过程判断高度差
  • 迭代：效率很低，不推荐
• 二叉树：找所有路径
  • 递归：前序，方便让父节点指向子节点，涉及回溯处理根节点到叶子的所有路径
  • 迭代：一个栈模拟递归，一个栈来存放对应的遍历路径
• 二叉树：递归中如何隐藏着回溯
  • 详解二叉树：找所有路径 中递归如何隐藏着回溯
• 二叉树：求左叶子之和
  • 递归：后序，必须三层约束条件，才能判断是否是左叶子。
  • 迭代：直接模拟后序遍历
• 二叉树：求左下角的值
  • 递归：顺序无所谓，优先左孩子搜索，同时找深度最大的叶子节点。
  • 迭代：层序遍历找最后一行最左边
• 二叉树：求路径总和
  • 递归：顺序无所谓，递归函数返回值为bool类型是为了搜索一条边，没有返回值是搜索整棵树。
  • 迭代：栈里元素不仅要记录节点指针，还要记录从头结点到该节点的路径数值总和

二叉树的修改与构造

• 翻转二叉树
  • 递归：前序，交换左右孩子
  • 迭代：直接模拟前序遍历
• 构造二叉树
  • 递归：前序，重点在于找分割点，分左右区间构造
  • 迭代：比较复杂，意义不大
• 构造最大的二叉树
  • 递归：前序，分割点为数组最大值，分左右区间构造
  • 迭代：比较复杂，意义不大
• 合合并两个二叉树
  • 递归：前序，同时操作两个树的节点，注意合并的规则
  • 迭代：使用队列，类似层序遍历

二叉搜索树的属性

• 二叉搜索树中的搜索(opens new window)
  • 递归：二叉搜索树的递归是有方向的
  • 迭代：因为有方向，所以迭代法很简单
• 是不是二叉搜索树(opens new window)
  • 递归：中序，相当于变成了判断一个序列是不是递增的
  • 迭代：模拟中序，逻辑相同
• 求二叉搜索树的最小绝对差(opens new window)
  • 递归：中序，双指针操作
  • 迭代：模拟中序，逻辑相同
• 求二叉搜索树的众数(opens new window)
  • 递归：中序，清空结果集的技巧，遍历一遍便可求众数集合
  • 二叉搜索树转成累加树(opens new window)
  • 递归：中序，双指针操作累加
  • 迭代：模拟中序，逻辑相同

二叉树公共祖先问题

• 二叉树的公共祖先问题
  • 递归：后序，回溯，找到左子树出现目标值，右子树节点目标值的节点。
  • 迭代：不适合模拟回溯
• 二叉搜索树的公共祖先问题
  • 递归：顺序无所谓，如果节点的数值在目标区间就是最近公共祖先
  • 迭代：按序遍历

二叉搜索树的修改与构造

• 二叉搜索树中的插入操作
  • 递归：顺序无所谓，通过递归函数返回值添加节点
  • 迭代：按序遍历，需要记录插入父节点，这样才能做插入操作
• 二叉搜索树中的删除操作
  • 递归：前序，想清楚删除非叶子节点的情况
  • 迭代：有序遍历，较复杂
• 修剪二叉搜索树
  • 递归：前序，通过递归函数返回值删除节点
  • 迭代：有序遍历，较复杂
• 构造二叉搜索树
  • 递归：前序，数组中间节点分割
  • 迭代：较复杂，通过三个队列来模拟
    tps://programmercarl.com/0106.从中序与后序遍历序列构造二叉树.html)
  • 递归：前序，重点在于找分割点，分左右区间构造
  • 迭代：比较复杂，意义不大
• 构造最大的二叉树
  • 递归：前序，分割点为数组最大值，分左右区间构造
  • 迭代：比较复杂，意义不大
• 合合并两个二叉树
  • 递归：前序，同时操作两个树的节点，注意合并的规则
  • 迭代：使用队列，类似层序遍历

二叉搜索树的属性

• 二叉搜索树中的搜索(opens new window)
  • 递归：二叉搜索树的递归是有方向的
  • 迭代：因为有方向，所以迭代法很简单
• 是不是二叉搜索树(opens new window)
  • 递归：中序，相当于变成了判断一个序列是不是递增的
  • 迭代：模拟中序，逻辑相同
• 求二叉搜索树的最小绝对差(opens new window)
  • 递归：中序，双指针操作
  • 迭代：模拟中序，逻辑相同
• 求二叉搜索树的众数(opens new window)
  • 递归：中序，清空结果集的技巧，遍历一遍便可求众数集合
  • 二叉搜索树转成累加树(opens new window)
  • 递归：中序，双指针操作累加
  • 迭代：模拟中序，逻辑相同

二叉树公共祖先问题

• 二叉树的公共祖先问题
  • 递归：后序，回溯，找到左子树出现目标值，右子树节点目标值的节点。
  • 迭代：不适合模拟回溯
• 二叉搜索树的公共祖先问题
  • 递归：顺序无所谓，如果节点的数值在目标区间就是最近公共祖先
  • 迭代：按序遍历

二叉搜索树的修改与构造

• 二叉搜索树中的插入操作
  • 递归：顺序无所谓，通过递归函数返回值添加节点
  • 迭代：按序遍历，需要记录插入父节点，这样才能做插入操作
• 二叉搜索树中的删除操作
  • 递归：前序，想清楚删除非叶子节点的情况
  • 迭代：有序遍历，较复杂
• 修剪二叉搜索树
  • 递归：前序，通过递归函数返回值删除节点
  • 迭代：有序遍历，较复杂
• 构造二叉搜索树
  • 递归：前序，数组中间节点分割
  • 迭代：较复杂，通过三个队列来模拟