3/26几何专题

1. 蓝桥杯真题-卡片（填空题）

小蓝有很多数字卡片，每张卡片上都是数字 0到 9。小蓝准备用这些卡片来拼一些数，他想从 1 开始拼出正整数，每拼一个，就保存起来，卡片就不能用来拼其它数了。小蓝想知道自己能从 1 拼到多少。例如，当小蓝有 30 张卡片，其中 0 到 9 各 3 张，则小蓝可以拼出 1 到 10，但是拼 11 时卡片 1 已经只有一张了，不够拼出 11。现在小蓝手里有 0 到 9 的卡片各 2021 张，共 202120210 张，请问小蓝可以从 11 拼到多少？提示：建议使用计算机编程解决问题。

import java.util.Scanner;
// 1:无需package
// 2: 类名必须Main, 不可修改

public class Main {
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        //在此输入您的代码...
        // 定义并初始化卡片集数组
        int[] cards = new int[10];
        for(int i = 0; i < cards.length; i++){
          cards[i] = 2021;
        }
        // 设置变量
        int num;  //当前正在拼的数
        int temp; //临时变量
        boolean flag = false;  //临时变量
        // 从1开始拼
        for(num = 1;;num++){
          // 对正在拼的数，查看每一位是什么数，若数组中有就-1，没有就跳出循环
          temp = num;
          while(temp != 0){
            if(cards[temp % 10] == 0){
              flag = true;
              break;
            }
            cards[temp % 10]--;
            temp /= 10;
          }
          // 没有对应的卡片可以拼了，跳出循环
          if (flag){
            break;
          }
        }
        // 输出可以拼到的数，num表示当前正在拼的数，因为当前这个数拼不出，所以应该输出前一个数（--num）
        System.out.println(--num);
        scan.close();
    }
}

2. 力扣-三锥形体投影面积

在 n x n 的网格 grid 中，我们放置了一些与 x，y，z 三轴对齐的 1 x 1 x 1 立方体。每个值 v = grid[i][j] 表示 v 个正方体叠放在单元格 (i, j) 上。现在，我们查看这些立方体在 xy 、yz 和 zx 平面上的投影。投影就像影子，将三维形体映射到一个 二维平面上。从顶部、前面和侧面看立方体时，我们会看到“影子”。返回所有三个投影的总面积 。

示例：

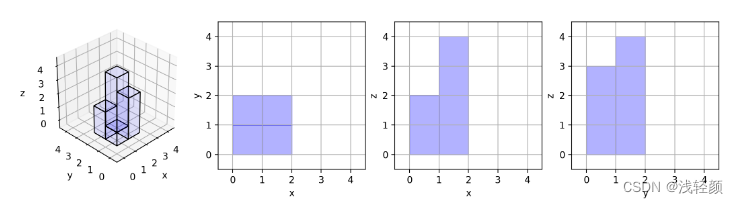
输入：[[1,2],[3,4]]

输出：17

解释：这里有该形体在三个轴对齐平面上的三个投影(“阴影部分”)。

class Solution {
    public int projectionArea(int[][] grid) {
        // 定义变量记录xy、yz、zx三个平面的投影面积
        int xyArea = 0, yzArea = 0, zxArea = 0;
        int n = grid.length;
        // xy平面上的投影面积为网格中非零元素的数目
        for(int i = 0; i < n; i++){
            for(int j = 0; j < n; j++){
                if(grid[i][j] > 0){
                    xyArea++;
                }
            }
        }
        // yz平面上的投影面积=每一列的最大高度之和
        for(int j = 0; j < n; j++){
            int height = 0;
            for(int i = 0; i < n; i++){
                height = Math.max(height,grid[i][j]);
            }
            yzArea += height;
        }
        // zx平面上的投影面积=每一行的最大高度之和
        for(int i = 0; i < n; i++){
            int height = 0;
            for(int j = 0; j < n; j++){
                height = Math.max(height,grid[i][j]);
            }
            zxArea += height;
        }
        // 三个投影的总面积
        return xyArea + yzArea + zxArea;
    }
}