基于机器学习的共享单车使用量分析与预测

七七四十九077

已于 2024-05-15 17:05:24 修改

阅读量6.1k

点赞数 56

分类专栏：机器学习大数据文章标签： python 开发语言 big data 机器学习随机森林回归

于 2024-05-14 18:08:00 首次发布

本文链接：https://blog.csdn.net/m0_64090099/article/details/138862987

版权

大数据同时被 2 个专栏收录

2 篇文章

订阅专栏

机器学习

1 篇文章

订阅专栏

第1章绪论

1.1课题研究背景及意义

1.1.1课题研究背景

自行车共享系统是新一代的传统自行车租赁，从会员，租赁到归还的整个过程已经自动化。通过这些系统，用户可以轻松地从特定位置租用自行车，然后在另一个位置返回。目前，全球约有500多个自行车共享计划，其中包括50多万辆自行车。今天，由于这些系统在交通、环境和健康问题中的重要作用，人们对它们产生了极大的兴趣。

1.1.2课题研究意义

除了自行车共享系统有趣的现实世界应用外，这些系统生成的数据特征使它们对研究具有吸引力。与公共汽车或地铁等其他运输服务相反，旅行的持续时间，出发和到达位置明确记录在这些系统中。此功能将自行车共享系统转变为可用于感知城市移动性的虚拟传感器网络。因此，预计通过监测这些数据可以检测到城市中的大多数重要事件。

数据预处理与特征选择

2.1数据集特征

2.1.1 数据集来源和说明

本项目数据集来源于kaggle关于国内共享自行车需求预测，资料信息产生时间段在2021-2022年之间，数据集存储在hour.csv文件中，主要属性及特征如下：

表2-1-1 数据集属性表
变量名	属性
instant	记录索引
dteday	日期
season	季节（1：冬季， 2：春季， 3：夏季， 4：秋季）
yr	年份（0： 2021， 1：2022）
mnth	月（1至12）
hr	小时（0 到 23）
holiday	假日
weekday	星期几
workingday	如果一天既不是周末也不是节假日，则为 1，否则为 0。
weathersit	1：晴朗，云少，部分多云，部分多云 2：雾+多云，薄雾+碎云，薄雾+少云，薄雾 3：小雪，小雨+雷雨+散云，小雨+散云 4：大雨+冰盘+雷雨+薄雾，雪+雾
temp	以摄氏度为单位的标准化温度。这些值通过（t-t_min）/（t_max-t_min）、t_min=-8、t_max=+39（仅按小时计）得出
atemp	以摄氏度为单位的归一化感觉温度。这些值是通过（t-t_min）/（t_max-t_min）、t_min=-16、t_max=+50（仅按小时计）得出的
hum	归一化湿度。值除以 100（最大值）
windspeed	归一化风速。值除以 67（最大值）
casual	临时用户数
registered	已注册用户数
CNT	租赁自行车总数，包括休闲自行车和注册自行车

2.1.2探索性数据分析

表2-1-2 数据集简单统计表
数据	count	mean	std	min	25%	50%	75%	max
Instant	17379.0000	8690.0000	5017.0295	1.0000	4345.5000	8690.0000	13034.5000	17379.0000
season	17379.000000	2.501640	1.10691	1.000000	2.000000	3.000000	3.000000	4.000000
yr	17379.000000	0.502561	0.500008	0.00000	0.000000	1.000000	1.000000	1.000000
mnth	17379.000000	6.537775	3.438776	1.000000	4.000000	7.000000	10.000000	12.000000
hr	17379.000000	11.546752	6.914405	0.000000	6.000000	12.000000	18.000000	23.000000
holiday	17379.000000	0.028770	0.167165	0.000000	0.000000	0.000000	0.000000	0.000000
weekday	17379.000000	3.003683	2.005771	0.000000	1.000000	3.000000	5.000000	6.000000
workingday	17379.000000	0.682721	0.465431	0.000000	0.000000	1.000000	1.000000	1.000000
weathersit	17379.000000	1.425283	0.639357	1.000000	1.000000	1.000000	2.000000	4.000000
temp	17379.000000	0.496987	0.192556	0.020000	0.340000	0.500000	0.660000	1.000000
atemp	17379.000000	0.496987	0.192556	0.020000	0.340000	0.500000	0.660000	1.000000
hum	17379.000000	0.627229	0.192930	0.000000	0.480000	0.630000	0.780000	1.000000
windspeed	17379.000000	0.190098	0.122340	0.000000	0.104500	0.194000	0.253700	0.850700
casual	17379.000000	35.676218	49.305030	0.000000	4.000000	17.000000	48.000000	367.000000
registered	17379.000000	153.786869	151.357286	0.000000	34.000000	115.000000	220.000000	886.000000
cnt	17379.000000	189.463088	181.387599	1.000000	40.000000	142.000000	281.000000	977.000000

2.2 数据预处理

2.2.1 缺失值处理

处理缺失值有两种常用的方法：第一种，直接删除法。对于缺失率较高的变量，可以认为这类变量是无效的，对整体数据影响较小，所以直接删除。第二种，填充缺失值。若缺失值不多，则数值型变量的缺失值可用中位数填补，而离散型变量的缺失值可用众数填补。如果缺失值比较多，又不想删去这个变量，那么可以将该变量的缺失值替换为指定的值，比如 0 或者-9999，其含义代表该变量为缺失值。

进一步，先根据 python 中的isnull.any()判断是否有空值，再根据 isnull().sum()方法观察数据的分布情况，具体操作如下：

df = pd.read_csv('hour.csv')

df.isnull().any()

df.isnull().sum()

结果显示，该数据集没有空值。

表2-2-1 数据集空值统计表
变量名	缺失率	变量名	缺失率
instant	0	workingday	0
casual	0	weathersit	0
cnt	0	temp	0
dteday	0	atemp	0
season	0	hum	0
yr	0	windspeed	0
holiday	0	casual	0
weekday	0	registered	0

2.2.2异常值处理

异常值，是指样本中的部分数值明显超过甚至小于样本中其余的观测数值。

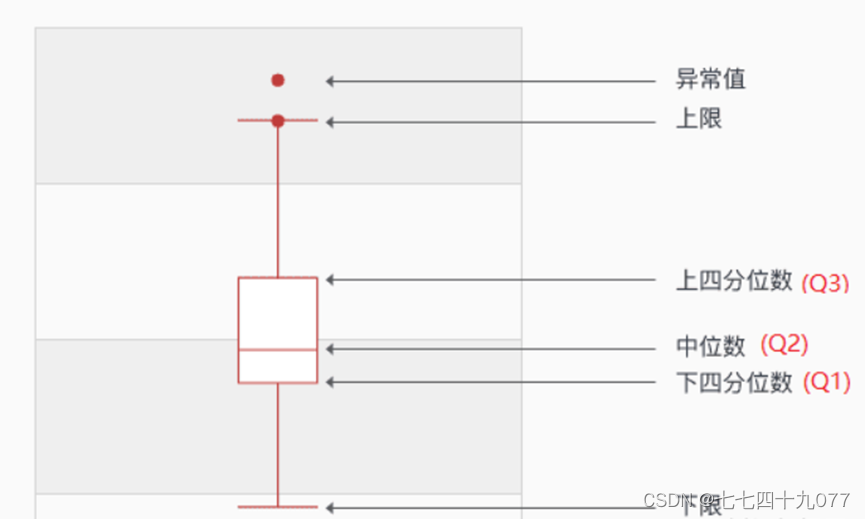
根据箱型图排除异常值，需要知道箱型图的上、下边界。其中涉及的几个概念简单的解释如下：

第三四分位数（Q3）：排序后比第三四分位数更大的值占总数据的25%。
第一四分位数（Q1）：排序后比第一四分位数更小的值占总数据的25%。
四分位距（IQR）：第三四分位的值减去第四分位的值，即Q3-Q1，这个区间内包含了50%的数据。
上边界：Q3 + 1.5 * IQR。
下边界：Q1 - 1.5 * IQR。

值大于上边界小于下边界的一般被认为异常值。

图2-2-1 箱型图示例

在本实验中，是对temp，atemp，windspeed,casual,registered,count这六列画出箱型图，查看是否有异常值。如图2-2-2所示，可以看出temp，atemp没有异常值需要处理，其他四项都有按箱型图标准判定的异常值。

图2-2-2 变量异常值情况

运用上述箱型图原理编写异常值判断函数sbnormalIndex()用于获取一个DataFrame的所有列中的异常值索引的并集，筛选出所有数据列的正常值交集，代码如下：

def abnormalIndex(df):

abnIndex = pd.Series().index

for i in range(len(col)):

s=df[col[i]]

a=s.describe()

high=a['75%']+(a['75%']-a['25%'])*1.5

low=a['75%']-(a['75%']-a['25%'])*1.5

abn=s[(s>high)|(s<low)]

print(col,list(abn.index))

abnIndex = abnIndex|abn.index

return abnIndex

df=df.drop(abnormalIndex(df))

2.2.3 变量交换

将一些与数字相关性不大的变量类型转化为category类型，实现代码如下：

cols=['season','month','hour','holiday',

'weekday','workingday','weather']

for col in cols:

df[col] = df[col].astype('category')

df.info()

2.3 数据分析

2.3.1数据可视化分析

（1）共享自行车在工作日和周末的使用情况特征分析

图2-3-1，图2-3-2，图2-3-3，图2-3-4中的标签0-6表示上周星期天到这周六，从下图中可以看出，在工作日人们使用和注册共享自行车的数量较多，其中一天中早上7:00-9:00和下午17:00-19:00这两个时间段使用和注册共享自行车的人员数量达到高峰期。而共享自行车未注册用户数量恰于其相反。说明了用户在工作日、特别是上下班高峰期对共享自行车的需求较大。

图2-3-1 工作日和周末不同时间段共享自行车使用数量点图

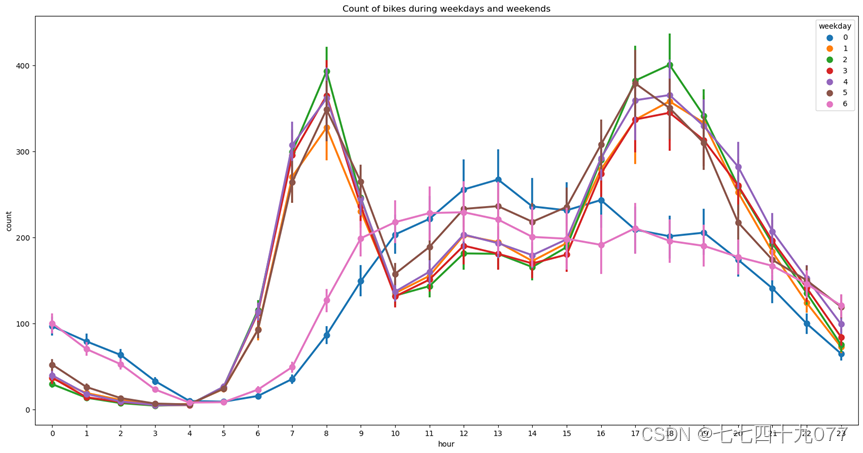
图2-3-2 工作日和周末在不同时间段共享自行车未注册用户数量点图

图2-3-3 工作日和周末共享自行车在不同时间段已注册用户数量点图

图2-3-4 工作日和周末不同时间段共享自行车使用数量分布柱状图

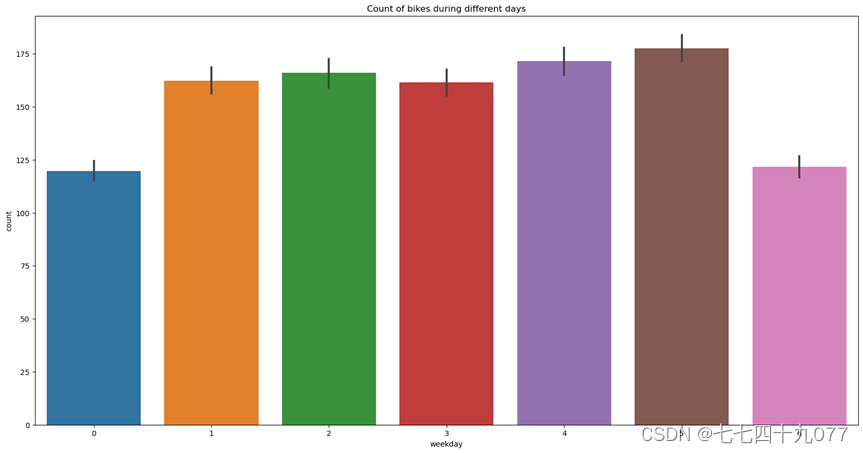
图2-3-5 不月份共享自行车使用者数量分布柱状图

（2）共享自行车在不同气候的使用情况特征分析

图2-3-6中的标签1-4代表天气，大致是晴天，多云，小雪/雨，大雨（具体见数据集属性），图2-3-7中的标签1-4代表季节，分别是春天，夏天，秋天，冬天。由图可以看出一年四季中在春天、秋天共享自行车的使用数量最多，而在晴天、阴天的天气中共享自行车的使用者数量也比较多。由此说明人们比较倾向于在气候凉爽，天气晴好的季节、天气中使用共享自行车。

图2-3-6 不同天气下共享自行车使用数量分布点图

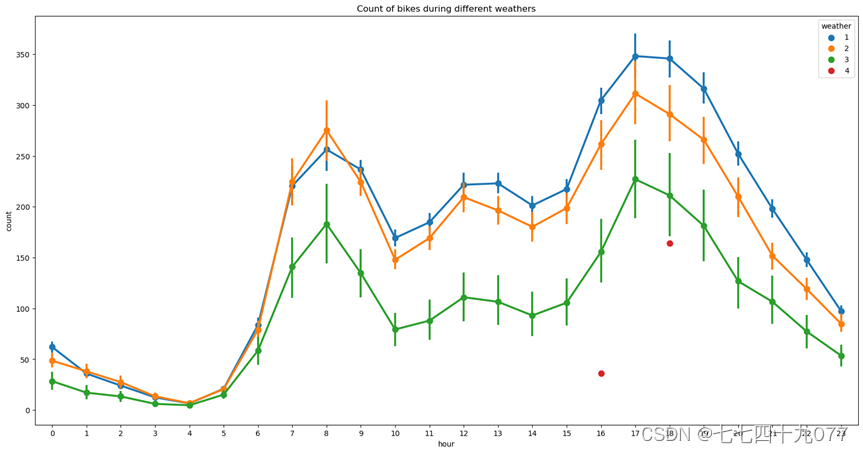
图2-3-7 不同季节下共享自行车使用者数量分布散点图

2.3.2数据相关性分析

绘制共享自行车与温度和气候的关系列线图：

图2-3-8 共享自行车与温度和气候的关系列线图

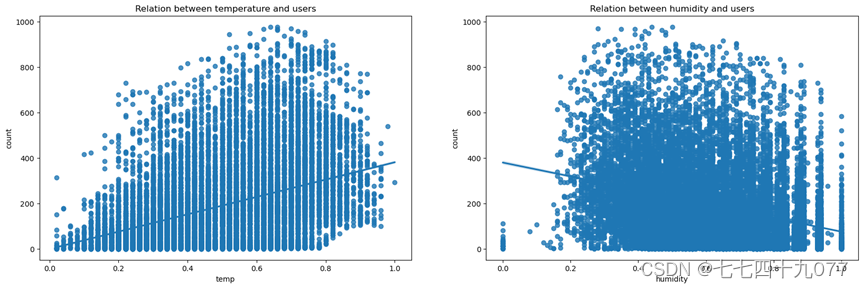
temp，atemp，windspeed,casual,registered,count维度数据的直方图绘制：

图2-3-9 各维度数据直方图

2.4特征工程

2.4.1特征选择

特征选择其目标是寻找最优特征子集。特征选择能剔除不相关(irrelevant)或冗余(redundant )的特征，从而达到减少特征个数，提高模型精确度，减少运行时间的目的[01]。另一方面，选取出真正相关的特征简化模型，协助理解数据产生的过程。从技术角度来看，数据挖掘中的特征选择是非常必要的。

本文筛选变量主要使用过滤法和嵌入法。首先使用互信息法的IV值结合Pearson相关系数法对特征进行初筛。然后根据LightGBM模型的特征重要性对变量进行精筛，最后确定入模的变量。

通过计算特征与特征之间的相关系数的大小，可判定两两特征之间的相关程度。取值区间在[-1, 1]之间，取值关系如下：corr(x1,x2)相关系数值小于0表示负相关(这个变量下降，那个就会上升)，即x1与x2是互补；corr(x1,x2)相关系数值等于0表示无相关；corr(x1,x2)相关系数值大于0表示正相关，即x1与x2是替代特征；
原理实现：取相关系数值的绝对值，然后把corr值大于90%~95%的两两特征中的某一个特征剔除。
如果两个特征是完全线性相关的，这个时候我们只需要保留其中一个即可。
因为第二个特征包含的信息完全被第一个特征所包含。此时，如果两个特征同时都保留的话，模型的性能很大情况会出现下降的情况。

基于公式(3-3)计算出WOE值，IV的计算公式如下：

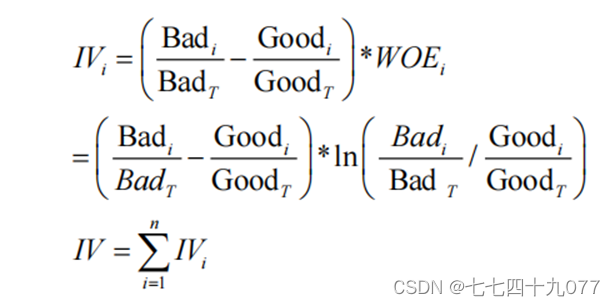
2.4.2特征处理

在统计学中，皮尔逊积矩相关系数用于度量两个变量X和Y之间的相关程度(线性相关)，其值介于-1与1之间，解释变量中出现某个解释变量可能被其他一个或者多个解释变量代替，这就是变量之间的线性关系[02]。若模型中的变量存在多重共线性的关系，很可能导致原来重要的解释变量被忽略，还会干扰其他变量的显著性，甚至对模型的稳定性和解释性造成影响。所以需要一个量化指标来衡量变量之间的相关性，由此引入Pearson相关系数，它可以衡量两个变量之间的相关性。其计算公式如下：

图2-4-1部分变量之间的皮尔逊积矩相关系数的相关系数热力图。

图2-4-1 各列数据的相关矩阵热力图

实现代码如下：

import seaborn as sns

corr = df.corr()

plt.figure(figsize=(20,15))

sns.heatmap(corr, annot=True, annot_kws={'size':15})

#查看各特征与count的相关系数

corr['count'].sort_values(ascending=False)

两个相关系数前面的负号表示这两个参数之间是负相关。各组属性之间彼此的相关性也比较高，这也表示应该进行主成分分析，选出有代表性的综合属性进行建模。从图中可以看出，选中和清洗的7列属性中的humidity，year，windspeed,temp,atemp都有较强的相关性。

2.4.3特征确定

根据数据的可视化分析以及通过相关系数的比较，最终确定特征属性为humidity，windspeed,temp,atemp。

2.5 数据标准化

探索性数据分析发现，各个变量特征的取值范围差异较大，即不同特征对

应不同的量纲，这样会干扰模型的预测精度，导致预测结果不准确。为了解决这个问题，在建模之前需要对数据标准化

2.5.1 one-hot编码

将离散型变量使用one-hot编码标准化，编码后的特征，其实每一维度的特征都可以看做是连续的特征。就可以跟对连续型特征的归一化方法一样，对每一维特征进行归一化。one-hot编码一般是通过M位状态寄存器来对M个状态进行编码，每个状态都有它独立的寄存位，并且在任意时候只有一位有效。让特征之间的距离计算更加合理。

代码实现：

pd.get_dummies(df['season'], prefix='season', drop_first=True)

df_oh = df

def one_hot_encoding(data, column):

data=pd.concat([data, pd.get_dummies(

data[column], prefix=column, drop_first=True)], axis=1)

data = data.drop([column], axis=1)

return data

cols=['season','month','hour','holiday','weekday',

'workingday','weather']

for col in cols:

df_oh = one_hot_encoding(df_oh, col)

df_oh.head()

第3章共享单车需求量基本模型构建

3.1训练/测试集划分

使用scikit的模型选择库中提供的train_test_split方法对自变量x和因变量y进行随机划分。参数test_size=0.25表明希望测试集占整个数据集的25%，那么训练集占整个数据的80%。参数ramdom_state=42指定了随机筛选中使用的随机数种子。之前将因变量count和自变量各个属性合并为一整个DataFrame 是为了数据清洗时能够同步清洗。现在为了划分训练集和测试集，又需要先将自变量和因变量拆开。

实现代码如下：

from sklearn.model_selection import train_test_split

import sklearn.metrics as sm

X = df_oh.drop(columns=['atemp', 'windspeed', 'casual', 'registered', 'count'], axis=1)

y = df_oh['count']

x_train, x_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=42)

data=pd.concat([train_x,train_y],axis=1)

print(data.shape)

3.2最优超参值

K折交叉验证用于模型调优，找到使得模型泛化性能最优的超参值。K折交叉验证使用了无重复抽样技术的好处：每次迭代过程中每个样本点只有一次被划入训练集或测试集的机会。使用数据集中的类标y_train初始化sklearn.cross_validation模块下的StratifiedKFold迭代器，通过n_folds参数设置块的数量。使用kfold在k个块中迭代时，使用train中返回的索引去拟合流水线，通过pipe_lr流水线保证样本都得到适当的缩放。

使用test索引计算模型的准确率。

图3-2-1 K折交叉验证模型

实现代码如下：

from sklearn import model_selection

def train(model):

kfold= model_selection.KFold(n_splits=5,

shuffle=True,random_state=42)

kfold = model_selection.KFold(n_splits=5, random_state=42)

pred = model_selection.cross_val_score(

model, X, y, cv=kfold, scoring='neg_mean_squared_error')

cv_score = pred.mean()

print('Model:',model)

print('CV score:', abs(cv_score))

for model in models:

train(model)

3.3 随机森林回归预测

随机森林算法是最常用也是最强大的监督学习算法之一，它兼顾了解决回归问题和分类问题的能力。随机森林是将多个决策树结合在一起，每次数据集是随机有放回的选出，同时随机选出部分特征作为输入的。下图展示了随机森林算法的具体流程结合器在分类问题中，选择多数分类结果作为最后的结果，在回归问题中，对多个回归结果取平均值作为最后的结果。可以看到随机森林算法是以决策树为估计器的Bagging算法。随机森林算法有很多的优势，包括以下 3 点。

训练完后的模型能够给出特征属性的重要性。
它是并行化的方法，速度比较快。
基于其随机性，模型不容易过拟合，抗噪声能力强。

3.3.1随机森林模型原理

随机森林是从原始训练样本集N中有放回地重复随机抽取k个样本生成新的训练样本集合，然后根据自助样本集生成k个分类树组成随机森林，新数据的分类结果按分类树投票多少形成的分数而定。其实质是对决策树算法的一种改进，将多个决策树合并在一起，每棵树的建立依赖于一个独立抽取的样品，森林中的每棵树具有相同的分布，分类误差取决于每一棵树的分类能力和它们之间的相关性。特征选择采用随机的方法去分裂每一个节点，然后比较不同情况下产生的误差。能够检测到的内在估计误差、分类能力和相关性决定选择特征的数目。单棵树的分类能力可能很小，但在随机产生大量的决策树后，一个测试样品可以通过每一棵树的。分类结果经统计后选择最可能的分类。下图展示了随机森林算法的具体流程。

图3-3-1 随机森林算法具体流程图

假设训练集 T 的大小为 N ，特征数目为 M ，随机森林的大小为 K ，随机森林算法的具体步骤如下：

遍历随机森林的大小 K 次：

从训练集 T 中有放回抽样的方式，取样N 次形成一个新子训练集 D

随机选择 m 个特征，其中 m < M

使用新的训练集 D 和 m 个特征，学习出一个完整的决策树

得到随机森林

3.3.2随机森林模型实践

共享单车数据中除了部分数值类型的特征之外，存在较多类别类型的特征，从特征情况来看比较适合使用随机森林来建模。使用scikit的模型选择库中提供的train_test_split方法对自变量x和因变量y进行随机划分。测试集占整个数据集的25%，那么训练集占整个数据的80%。使用随机森林的调优超参数，使用有监督学习fit()，将训练数据在模型中训练一定次数，返回loss和测量指标。

实现代码如下：

model = RandomForestRegressor() # 随机森林特有的参数，调优超参数

model.fit(x_train, y_train) # 有监督学习fit（），将训练数据在模型中训练一定次数，返回loss和测量指标

y_pred = model.predict(x_test) # 数据x_test放到模型中预测

3.4 建立线性回归模型

skleam的linear model库中提供了很多线性回归的算法，这里采用最基础的梯度下降回归器SGDRegressor。linear_mode里面提供的LinearRegression是使用矩阵计算最小二乘算法[02]，在模型简单、数据量不大的情况下更快，但是梯度下降数值优化的算法通用性更强。

实现代码如下：

from skleam.linear model import SGDRegressor
sgd = SGDRegressor()
sgd.fit(x_train_std,y_train_std)

print(sgd.coef，sgd.intercept)

3.5 模型评估

在随机森林模型中用MSE(均方误差）作为评价指标。测试集的均方误差为0.48595。模型在测试集上准确率达到0.891448。都处在一个比较合理的范围，但改进空间很大。

将训练模型和预测预测模型误差差分布画成散点图：

图3-5-1 训练模型和预测预测模型误差差散点图

实现代码如下：

error = y_test - y_pred

fig, ax = plt.subplots()

ax.scatter(y_test, error)

ax.axhline(lw=3, color='black')

ax.set_xlabel('Observed')

ax.set_ylabel('Error')

plt.show()

3.6模型优化

3.6.1 Min-Max标准化

min-max标准化方法是对原始数据进行线性变换。设minA和maxA分别为属性A的最小值和最大值，将A的一个原始值x通过min-max标准化映射成在区间[0,1]中的值x'，其公式为：

代码实现：

#数值特征标准化

numerialFeatureNames=['temp','humidity']

#MinMax标准化

from sklearn.preprocessing import MinMaxScaler

scaler=MinMaxScaler()

scaler.fit(data[numerialFeatureNames])

data[numerialFeatureNames]=scaler.transform(data[numerialFeatureNames])

3.6.2 模型再优化

并过滤掉不必要的特征值，实现代码如下：

#构造验证集

dataTest=pd.concat([train_x,train_y],axis=1)

#目标与数据分离，删除不必要的特征

train_x = data.copy().drop(["count"], axis=1)

train_y = data["count"]

test_x = dataTest.copy().drop(["count"], axis=1)

test_y = dataTest["count"]

#重新建模预测需求的自行车数量

#重新训练模型

model = RandomForestRegressor()

model.fit(train_x,train_y)

pred_y = model.predict(test_x)

#在验证集上验证

from sklearn.metrics import mean_squared_error

print("RandomForestRegressor mean_squared_error:",mean_squared_error(pred_y,test_y))

print("RandomForestRegressor explained_variance_score:",sm.explained_variance_score(pred_y,test_y))

np.sqrt(mean_squared_error(test_y, pred_y))

3.6.3 优化结果

表4-4-1
	优化前	优化后
MSE	0.4859536324223761	0.2743996137438867
MRA	0.8914484688058553	0.966075171974046

第5章总结

通过对kaggle关于国内共享自行车在2021-2022年产生的数据，综合采用线性回归、岭回归、随机森林和梯度提升回归等八个模型进行训练，通过预测模型比较，选出随机森林预测模型作为最终的共享单车需求量预测模型。本文探讨共享单车需求预测的影响因素和模型设计问题。主要工作包括：对数据进行缺失值、去重、异常值的处理，通过相关系数法以及数据可视化分析，选出特征值；使用scikit的模型选择库中提供的train_test_split方法对自变量x和因变量y进行随机划分。测试集占整个数据集的25%，那么训练集占整个数据的80%。将离散型变量使用one-hot编码标准化之后，构建随机森林预测模型。对原始数据惊醒Min-max标准化处理后，获得测试集的均方误差为0.27。模型在测试集上准确率达到0.96。使用该模型未进行Min-max标准化前，测试集的均方误差为0.48。模型在测试集上准确率0.89。说明该预测模型预测能力相当。