伽玛函数,也叫欧拉第二积分,是阶乘函数在实数与复数上扩展的一类函数。
伽玛函数作为阶乘函数的延拓,是定义在复数范围内的亚纯函数,通常写成,负整数和0是它的一阶极点。
实数域:

复数域:
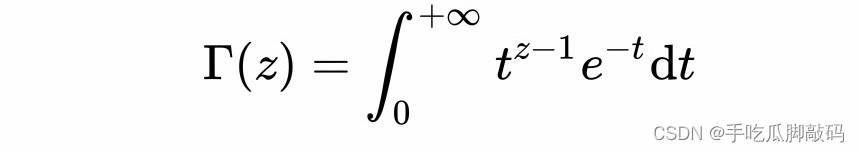

在解题中,伽马函数作为简化计算的一种方法。
其中常用的两条性质:

其中我们将伽马函数转换成容易理解的形式,推导如下:

由此看来通过转变使表达式更容易理解~
下面是一道例题

很明显,根据题目给的结构应将x替换
 然后再代入原式
然后再代入原式
伽玛函数,也叫欧拉第二积分,是阶乘函数在实数与复数上扩展的一类函数。
伽玛函数作为阶乘函数的延拓,是定义在复数范围内的亚纯函数,通常写成,负整数和0是它的一阶极点。
实数域:

复数域:
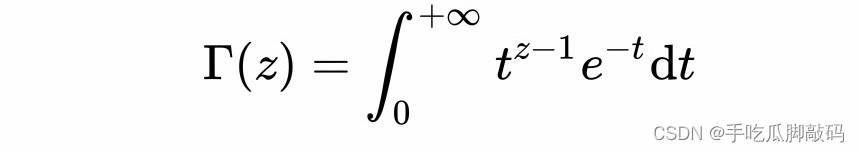

在解题中,伽马函数作为简化计算的一种方法。
其中常用的两条性质:

其中我们将伽马函数转换成容易理解的形式,推导如下:

由此看来通过转变使表达式更容易理解~
下面是一道例题

很明显,根据题目给的结构应将x替换
 然后再代入原式
然后再代入原式
 673
673
 6090
6090











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


