本人ctf新手,这个比赛已经过去快半年了,因为对于密码学的一道题始终无法理解,再后面的慢慢摸索中,终于理顺了所有思路,在此将这个迟来的wp与大家共同分享学习。
Misc
1、火锅链观光打卡


签到题,理论题,答对7道有flag
2、神秘文件
解压题目压缩包,得到

part4
打开ppt
很明显看到一个密文

密文UGFSdDQ6NmYtNDA=,很明显的base64编码特征
--------------
注:base64编码特征:
采用6个比特位进行切割编码,编码索引表由A~Z,a~z,0~9,“+”,“/“依次排列组成,共计64个可见字符。
base64编码一共要表示64个字符,那么需要6bit,也就是2^6=64,即000000-111111,base64的核心思想就是,将3个字节(1字节8bit)拆分成4个6bit,然后对每个6bit的高位补2个0,构成1个字节。也即是每3个字节最终结果将变成4个字节。如果原始字符串的字节数不是3的整数倍,那么就用0来填充,用来填充的0就被编码成了'=',这就是出现=的原因,并且只会出现在结果中,如果原始字符刚好是3字节的整数倍,那么就没有等号了,即=作为填充字符
--------------
进行解码,得到 PaRt4:6f-40

第5张ppt缩小,看到两个加密字符

part6
第一个加密字符:UGFyVDY6ZC0y
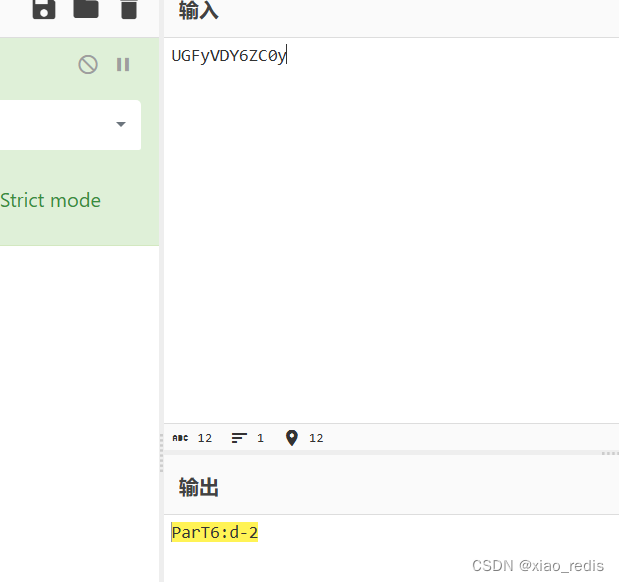
同样base64解码,得到:ParT6:d-2
part5
备注里面,这样的信息

由N round Base64猜测是base64循环解码
7次循环解码后得到,pArt5:5f-90d

part10
到第4张ppt,打开批注,发现
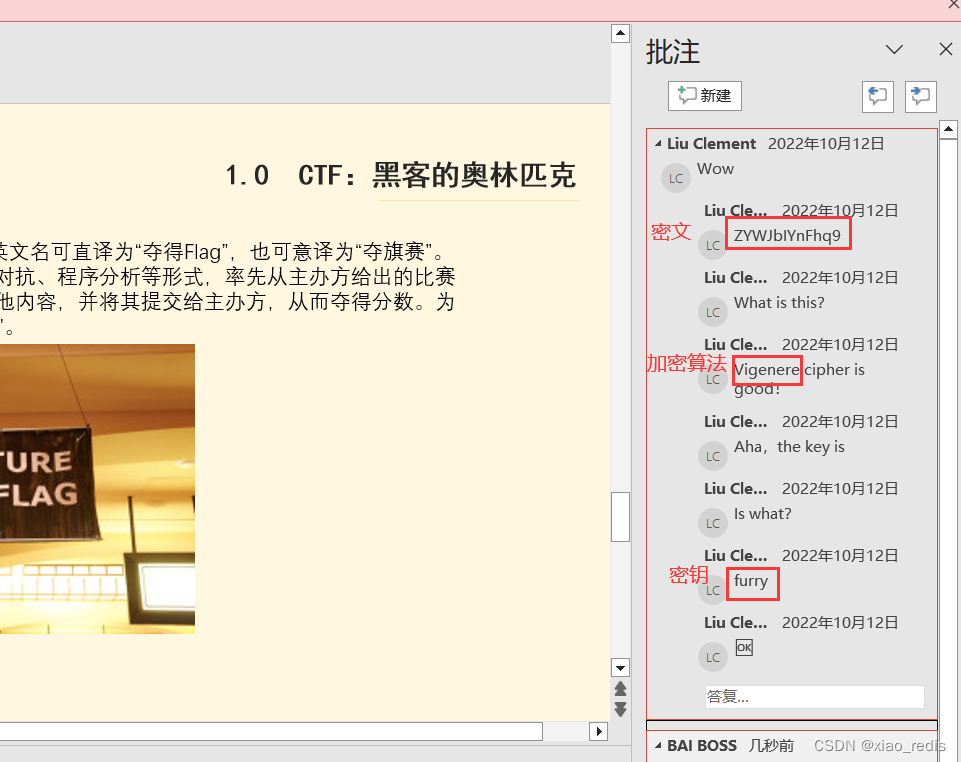
由对话得出密文UEFSdDEwOjl9、加密算法是维吉尼亚、密钥furry
解密得出,PARt10:9}

发现第二张ppt左上角有个东西

放大

似乎没什么其他信息
第5张找到一张隐藏图片,但似乎缺少一部分

part1
在ppt详细信息里发现
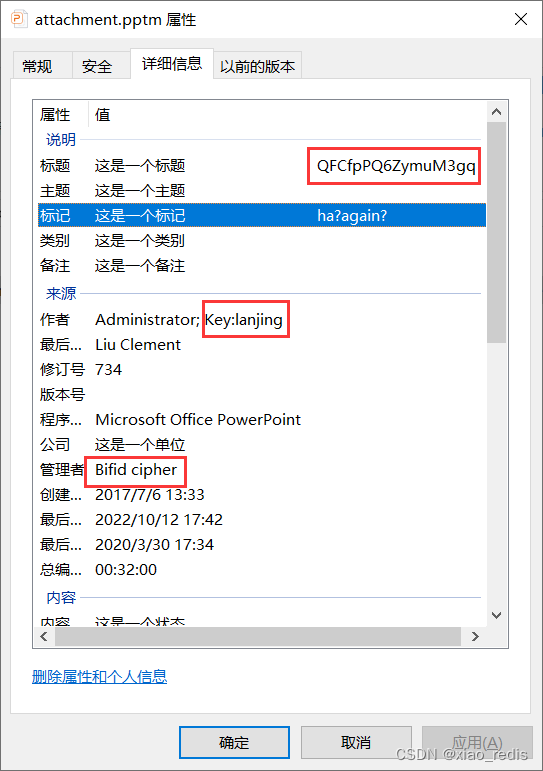
密文QFCfpPQ6ZymuM3gq,加密类型Bifid,密钥lanjing

bifid解密后再次basr64解码,得到Part1:flag{e
part7
第4张ppt打开窗格

得到密文编码字符串:HRSFIQp9ZwWvZj==,加密方式ROT13,进行ROT13置换解密后尝试base64解密得到PART7=22b3

part8
点击视图,打开幻灯片母版,移开全黑那张幻灯片的背景
看到编码字符串:c1GFSbd3Dg6BODbdl,根据提示Remove All ↓’B ’/’b’ /’1 ’/’3’,去掉Bb13后进行base64解码,得到paRt8:87e

part3
在ppt里面点击alt+f11进入宏编辑界面
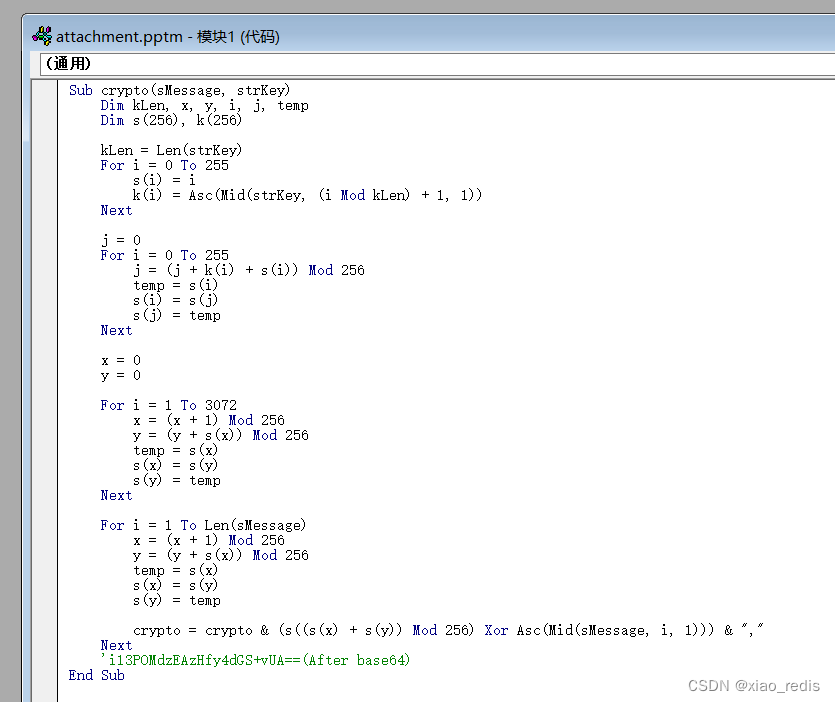
由代码得出,应该是某部分flag经过了RC4加密后又base64编码,最后给出了i13POMdzEAzHfy4dGS+vUA==,可以看到RC4加密并没有给出密钥key,
网上还有大佬使用了c语言脚本解密,大家有兴趣可以去看看
第十七届全国大学生信息安全竞赛CISCN线上赛部分Writeup - NYNUSEC
先进行base64解码,然后尝试RC4解密,得到
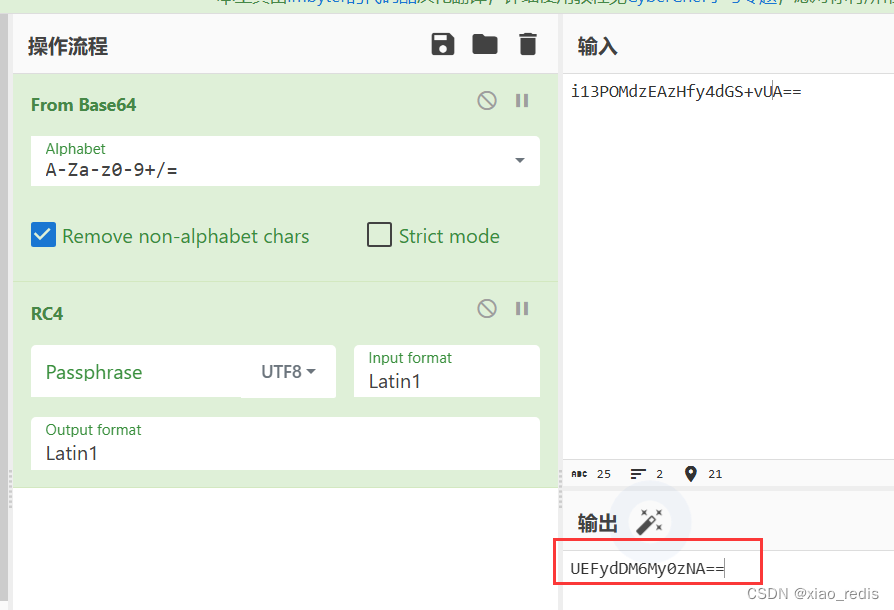
发现base64特征,再次base64解码,得到PArt3:3-34

到这里,已经找到了
Part1:flag{e
PArt3:3-34
PaRt4:6f-40
pArt5:5f-90d
ParT6:d-2
PART7=22b3
paRt8:87e
PARt10:9}
差2和9,还记得前面有一个凯撒相关的文字和一张不全的图片,如下图


下面将pptm后缀改为zip,得到

part9
查找文件,在\ppt\media下找到完整的图片

密文cGFyVDk6ZGVI,疑似base64,进行解码,解码后得到

但是注意,得到的是deH,含有大写,一般flag都是小写字母,猜测将最后一位大写I改为小写l(就是大写L)

修改后得到parT9:dee
Part2
然后再ppt\embeddings路径下找到word文档,但打开后依然看不到明显的信息

将word文档修改后缀位zip,在word/document.xml中发现

可以看到密文mQPinNS6Xtm1JGJs,加密方式已经提示是凯撒加密,偏移量ffset为10,下面进行解密
先凯撒解密,得到cGFydDI6Njc1ZWZi
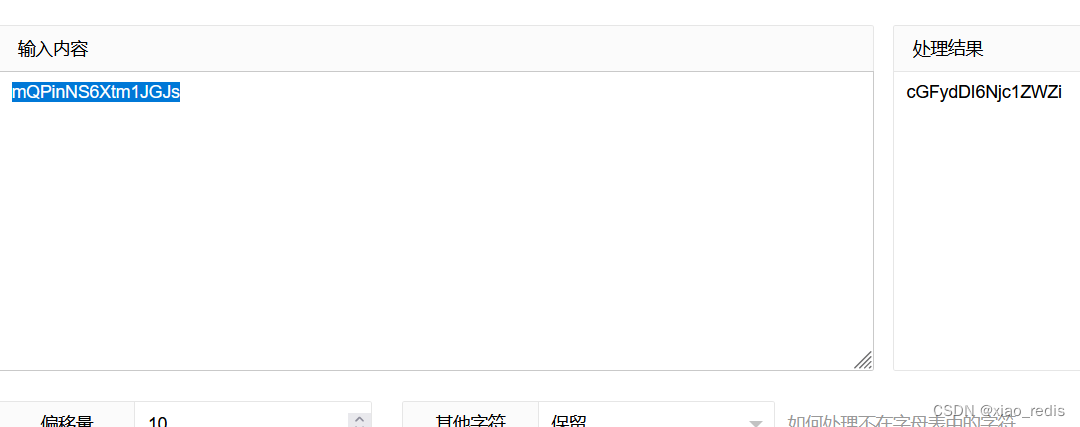
再base64解密,得到part2:675efb

至此,全部找到,最终flag,flag{e675efb3-346f-405f-90dd-222b387edee9}
格式为常见uuid格式8-4-4-4-12,共32位。
Crypto
1、OvO
题目代码:
from Crypto.Util.number import *
from secret import flag
nbits = 512
p = getPrime(nbits)
q = getPrime(nbits)
n = p * q
phi = (p-1) * (q-1)
while True:
kk = getPrime(128)
rr = kk + 2
e = 65537 + kk * p + rr * ((p+1) * (q+1)) + 1
if gcd(e, phi) == 1:
break
m = bytes_to_long(flag)
c = pow(m, e, n)
e = e >> 200 << 200
print(f'n = {n}')
print(f'e = {e}')
print(f'c = {c}')
"""
n = 111922722351752356094117957341697336848130397712588425954225300832977768690114834703654895285440684751636198779555891692340301590396539921700125219784729325979197290342352480495970455903120265334661588516182848933843212275742914269686197484648288073599387074325226321407600351615258973610780463417788580083967
e = 37059679294843322451875129178470872595128216054082068877693632035071251762179299783152435312052608685562859680569924924133175684413544051218945466380415013172416093939670064185752780945383069447693745538721548393982857225386614608359109463927663728739248286686902750649766277564516226052064304547032760477638585302695605907950461140971727150383104
c = 14999622534973796113769052025256345914577762432817016713135991450161695032250733213228587506601968633155119211807176051329626895125610484405486794783282214597165875393081405999090879096563311452831794796859427268724737377560053552626220191435015101496941337770496898383092414492348672126813183368337602023823
"""解题思路:
给出了n、e、c,但e被抹去了低200位,n无法分解
观察e的构造过程,
e = 65537 + kk * p + rr * ((p+1) * (q+1)) + 1
则e = 65537 + kk * p + rr * [p * q + p + q + 1] + 1
则e = 65537 + kk * p + rr * n + rr * [p + q + 1] + 1
则e = rr * n + 65537 + kk * p+ rr * [p + q + 1] + 1
又因为已知的e没有低200位,则记为eh,e的低200位记为el
则eh + el = rr * n + 65537 + kk * p+ rr * [p + q + 1] + 1
即1152位 = 128位 * 1024位 + 最高640位
记为eh + el = rr * n + t,即t=65537 + kk * p+ rr * [p + q + 1] + 1
则eh = rr * n + (t - el)
转换一下:eh / n = rr 余 t - el,
即利用带余除法得到rr,进一步得到kk
rr = eh // n,//为严格除,即忽略余数
kk = rr - 2
这里得到kk和rr,再次观察e 的生成过程
e = 65537 + kk * p + rr * ((p+1) * (q+1)) + 1
将e写成eh,即
eh ≈ 65537 + kk * p + rr * ((p+1) * (q+1)) + 1
在这个式子的两边同时乘以q,得到
eh * q ≈ 65537 * q + kk * n + rr * n * q + rr * (n + q^2 + q) + q
根据这个式子构造关于q的高位的二次多项式求解,即
eh * qh ≈ 65537 * qh + kk * n + rr * n * qh + rr * (n + qh^2 + qh) + qh
则f = 65537 * qh + kk * n + rr * n * qh + rr * (n + qh^2 + qh) + qh - eh * qh
在实数域内求解,得到q的高位
再使用Coppersmith得到q,即可求出flag
解题脚本:
# sagemath
from Crypto.Util.number import *
n = 111922722351752356094117957341697336848130397712588425954225300832977768690114834703654895285440684751636198779555891692340301590396539921700125219784729325979197290342352480495970455903120265334661588516182848933843212275742914269686197484648288073599387074325226321407600351615258973610780463417788580083967
e = 37059679294843322451875129178470872595128216054082068877693632035071251762179299783152435312052608685562859680569924924133175684413544051218945466380415013172416093939670064185752780945383069447693745538721548393982857225386614608359109463927663728739248286686902750649766277564516226052064304547032760477638585302695605907950461140971727150383104
c = 14999622534973796113769052025256345914577762432817016713135991450161695032250733213228587506601968633155119211807176051329626895125610484405486794783282214597165875393081405999090879096563311452831794796859427268724737377560053552626220191435015101496941337770496898383092414492348672126813183368337602023823
eh = e # 高位e
kk = eh//n - 2
rr = kk + 2
PR.<q> = PolynomialRing(RealField(1000)) # 精度位1000的实数域
f = 65537*q + kk * n + rr*(n*q+q^2+n+q) + 1*q - eh*q # 构造的关于q高位的二次多项式
res = f.roots() # 得到二次多项式的根
qh = int(res[0][0]) # 抹去根的小数部分,得到q的高位
# coopersmith攻击得q
PR.<x> = PolynomialRing(Zmod(n)) # 定义了一个以 x 为变量的多项式环,并且所有的系数都将在模 n 的范围内进行运算。
f = qh + x # 多项式f
res = f.small_roots(X=2^210,beta=0.499,epsilon = 0.03)
# Coppersmith's Small Root Algorithm ,
# X=2^210,x 的值在 2^210 以内进行搜索
# beta = 0.499 表示要寻找的是 x,其值应当是模数 n 的大约 n^0.499 的数量级(非常接近于模数 n 的一半)。这表明 x 相对较小,但接近 n 的一半大小。
# epsilon=0.03,允许 3% 的误差范围。较小的 epsilon 值意味着要求更高的精度
q = GCD(qh+int(res[0]),n) # int(res[0])将得到的解转换为整形,与q的高位相加,并与n求最大公约数,即为q
p = n // q
e = 65537 + kk * p + rr * ((p+1) * (q+1)) + 1 # 求真值e
print(long_to_bytes(int(pow(c,inverse(e,(p-1)*(q-1)),n)))) # 求flag
# b'flag{b5f771c6-18df-49a9-9d6d-ee7804f5416c}'这道题的关键点有三个
1、通过e的生成式,构造带余除法,得到rr和kk
2、通过e的生成式,构造关于q高位的二次多项式,在实数域内进行求解二次多项式,得到q的高位
3、通过coopersmith小根算法在以x为变量的多项式环,在模n的范围内,求解出q的低位,得到完整的q
4、常规RSA解密
2、古典密码
赛题密码:
AnU7NnR4NassOGp3BDJgAGonMaJayTwrBqZ3ODMoMWxgMnFdNqtdMTM9
先用埃特巴什码(Atbash Cipher)解密

再用base64进行解码
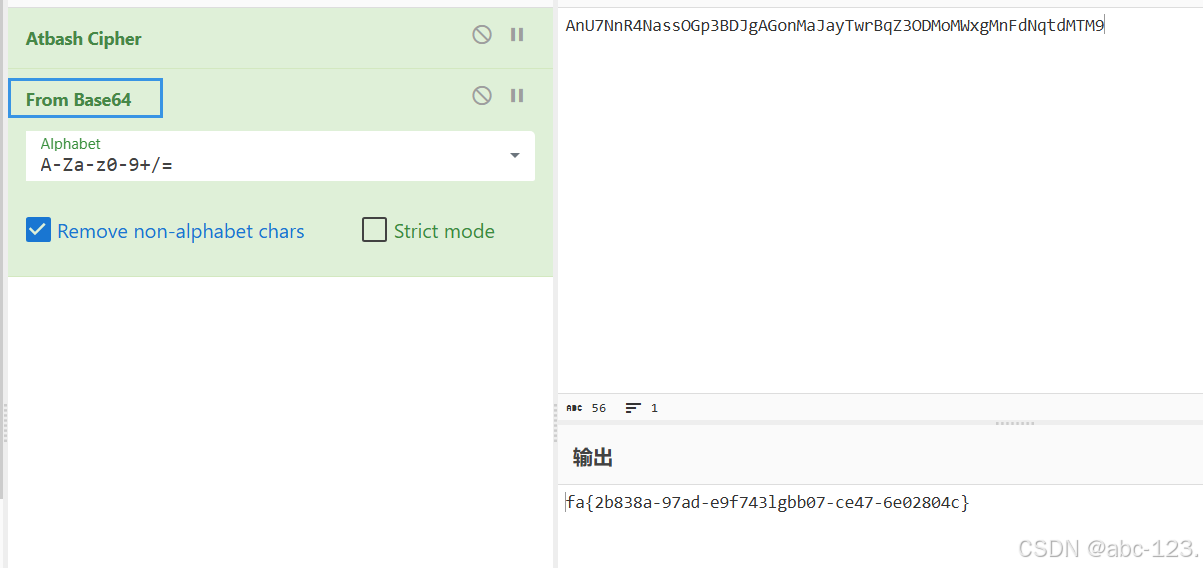
最后使用2栏栅栏解密

得到flag
参考文章:
https://www.nynusec.com/post/1001/
第十七届全国大学生信息安全竞赛创新实践能力赛初赛(CISCN-2024部分WP)_ciscn2024 web-CSDN博客
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








