-
计算极限 lim n → ∞ 2024 n ( 1 − cos 1 n 2 ) n 3 1 + n 2 − n \mathop {\lim }\limits_{n \to \infty } \frac{ {\sqrt[n]{ {2024}}\left( {1 - \cos \frac{1}{ { {n^2}}}} \right){n^3}}}{ {\sqrt {1 + {n^2}} - n}} n→∞lim1+n2−nn2024(1−cosn21)n3
lim n → ∞ 2024 n ( 1 − cos 1 n 2 ) n 3 1 + n 2 − n = lim n → ∞ 1 2 ( 1 n 2 ) 2 n 3 ( 1 + n 2 + n ) 1 lim n → ∞ 2024 n = 1 \begin{align*} \lim_{n \to \infty} \frac{\sqrt [n]{2024} \left( 1 - \cos \frac{1}{n^2} \right) n^3}{\sqrt{1 + n^2} - n} &= \lim_{n \to \infty} \frac{\frac{1}{2} \left( \frac{1}{n^2} \right)^2 n^3 \left( \sqrt{1 + n^2} + n \right)}{1} \lim_{n \to \infty} \sqrt [n]{2024} \\ &= 1 \end{align*} n→∞lim1+n2−nn2024(1−cosn21)n3=n→∞lim121(n21)2n3(1+n2+n)n→∞limn2024=1
-
计算定积分 ∫ 0 π cos 2 x e x d x \int_0^\pi \cos^2 x e^x \, \mathrm{d}x ∫0πcos2xexdx
∫ 0 π cos 2 x e x d x + ∫ 0 π sin 2 x e x d x = ∫ 0 π e x d x = e π − 1 ∫ 0 π cos 2 x e x d x − ∫ 0 π sin 2 x e x d x = ∫ 0 π cos 2 x e x d x = ( k 1 cos 2 x + k 2 sin 2 x ) e x ∣ 0 π \begin{align*} \int_0^\pi \cos^2 x e^x \, \mathrm{d}x + \int_0^\pi \sin^2 x e^x \, \mathrm{d}x &= \int_0^\pi e^x \, \mathrm{d}x \\ &= e^\pi - 1 \\ \int_0^\pi \cos^2 x e^x \, \mathrm{d}x - \int_0^\pi \sin^2 x e^x \, \mathrm{d}x &= \int_0^\pi \cos 2x e^x \, \mathrm{d}x \\ &= \left( k_1 \cos 2x + k_2 \sin 2x \right) e^x \bigg|_0^\pi \end{align*} ∫0πcos2xexdx+∫0πsin2xexdx∫0πcos2xexdx−∫0πsin2xexdx=∫0πexdx=eπ−1=∫0πcos2xexdx=(k1cos2x+k2sin2x)ex 0π
由方程组 k 1 + 2 k 2 = 1 {k_1} + 2{k_2} = 1 k1+2k2=1, k 2 − 2 k 1 = 0 {k_2} - 2{k_1} = 0 k2−2k1=0 可得 k 1 = 1 5 {k_1} = \frac{1}{5} k1=51, k 2 = 2 5 {k_2} = \frac{2}{5} k2=52。
( 1 5 cos 2 x + 2 5 sin 2 x ) e x ∣ 0 π = 1 5 ( e π − 1 ) \begin{align*} \left( \frac{1}{5} \cos 2x + \frac{2}{5} \sin 2x \right) e^x \bigg|_0^\pi &= \frac{1}{5} \left( e^\pi - 1 \right) \end{align*} (51cos2x+52sin2x)ex 0π=51(eπ−1)
故原式为 3 5 ( e π − 1 ) \frac{3}{5} \left( e^\pi - 1 \right) 53(eπ−1)。
-
计算曲线积分
∮ C y 1 + x 2 d x + ( 4 x + ln ( x + 1 + x 2 ) ) d y \oint_C \frac{y}{\sqrt{1 + x^2}} \, \mathrm{d}x + \left( 4x + \ln \left( x + \sqrt{1 + x^2} \right) \right) \, \mathrm{d}y ∮C1+x2ydx+(4x+ln(x+1+x2))dy其中曲线 C C C 为从 A ( 1 , 0 ) A(1,0) A(1,0) 到 B ( − 1 , 0 ) B(-1,0) B(−1,0) 的上半圆周,方向为逆时针。
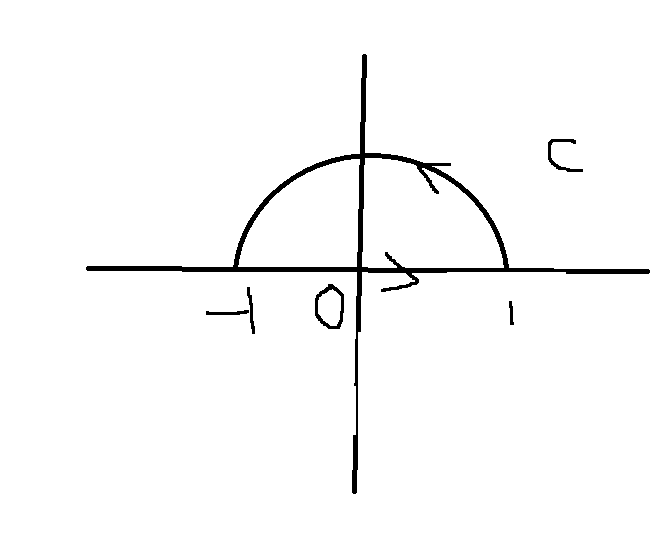
∮ C y 1 + x 2 d x + ln ( x + 1 + x 2 ) d y = ∮ C 4 x d y = ∫ 0 π 4 cos 2 θ d θ = ∫ 0 π 2 ( cos 2 θ + 1 ) d θ = 2 π \begin{align*} \oint_C \frac{y}{\sqrt{1 + x^2}} \, \mathrm{d}x + \ln \left( x + \sqrt{1 + x^2} \right) \, \mathrm{d}y &= \oint_C 4x \, \mathrm{d}y \\ &= \int_0^\pi 4 \cos^2 \theta \, \mathrm{d}\theta \\ &= \int_0^\pi 2 \left( \cos 2\theta + 1 \right) \, \mathrm{d}\theta \\ &= 2\pi \end{align*} ∮C1+x2ydx+ln(x+1+x2)dy=∮C4xdy=∫0π4cos
2024数学分析【南昌大学】
于 2024-10-26 21:50:36 首次发布








 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章



















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










