数据结构与算法05堆|建堆|Top-k问题

目录

一、堆

1、堆的介绍

2、堆的常用操作

3、堆的实现

3.1堆的存储与表示

3.2、堆的元素插入

3.3、堆顶元素出堆

3.4代码

 4、堆的常见应用

 二、建堆操作

1、借助入堆操作实现

2、通过遍历堆化实现

复杂度分析

三、Top-k问题

解法1：遍历/迭代

 解法2：排序

解法3：基于堆的解法

四、交换两个元素值

方法1

方法2

方法3

 3.1算术运算

3.1.1加减法

3.1.2乘除法

方法4

---

一、堆

1、堆的介绍

    堆（heap）是一种满足特定的条件的完全二叉树，主要可以分为大根堆和小根堆。

• 大根堆（max heap）：任意节点的值大于等于其子节点的值。
• 小根堆（min heap）：任意节点的值小于等于其子节点的值。

 由于堆作为完全二叉树的一个特例，故其具有以下的特性，

1、最深一层的节点靠左填充，且前面所有层地节点均被填满。

2、将完全二叉树的根节点称为堆顶，将底层最靠右的节点称为堆底。

3、对于大根堆/小根堆，堆顶元素的值是最大/最小的。

2、堆的常用操作

    需要指出的是，许多编程语言提供的是优先队列（priority queue），这是一种抽象的数据结构，定义为具有优先级排序的队列。

 实际上，堆通常用于实现优先队列，大顶堆相当于元素按从大到小的顺序出队的优先队列。从使用角度来看，我们可以将“优先队列”和“堆”看作等价的数据结构。因此，本书对两者不做特别区分，统一称作“堆”。

import heapq

# 初始化小顶堆
min_heap, flag = [], 1
# 初始化大顶堆
max_heap, flag = [], -1

# Python 的 heapq 模块默认实现小顶堆
# 考虑将“元素取负”后再入堆，这样就可以将大小关系颠倒，从而实现大顶堆
# 在本示例中，flag = 1 时对应小顶堆，flag = -1 时对应大顶堆

heapq.heappush(max_heap,flag * 1)
heapq.heappush(max_heap,flag * 3)
heapq.heappush(max_heap,flag * 2)
heapq.heappush(max_heap,flag * 5)
heapq.heappush(max_heap,flag * 4)

# 获取堆顶元素
peek:int = flag * max_heap[0]
print(f"堆顶元素为{peek}")

size:int = len(max_heap)
print(f"堆的大小为{size}")

print("输出大顶堆为",end="")
# 堆顶元素出堆，会按照从大到小的顺序输出
for i in range(len(max_heap)):
    val = flag * heapq.heappop(max_heap)
    print(val,end="")

print()
is_empty:bool = not max_heap
print(f"当前堆是否为空{is_empty}")

# 输入列表并建堆
min_heap:list[int] = [1,3,2,5,4]
heapq.heapify(min_heap)
print(f"小顶堆对应的列表为{min_heap}")

3、堆的实现

    下文实现的是大顶堆，若要将其转化为小顶堆则只需要将对应的大于等于改为小于等于即可。

3.1堆的存储与表示

    在之前的二叉树章节中提到过，完全二叉树非常适合用数组表示，由于堆正好是一种完全二叉树，所以我们用数组的形式存储堆。

当使用数组表示二叉树时，元素代表节点值，索引代表节点在二叉树中的位置。节点指针通过索引映射公式来实现。

如图 8-2 所示，给定索引 i ，其左子节点的索引为 2i+1 ，右子节点的索引为 2i+2 ，父节点的索引为 (i−1)/2（向下整除）。当索引越界时，表示空节点或节点不存在。

 堆的基本存储就是如上所示，查找当前节点i对应的左子节点，右子节点，以及其父节点都不过多讲述了，与二叉树的数组存储一样，还有求当前的堆顶元素，堆的大小等都在3.4的代码中展示，轻而易举就能看懂，下面着重讲解一下，堆的插入元素以及堆顶元素出堆的操作：

3.2、堆的元素插入

    给定一个任意元素要将其插入堆中，首先应把这个元素放到堆底，添加后，由于是大顶堆，需要判断新加入的元素是否破坏了原本的大顶堆的结构，若破坏了（新插入的元素值大于其父节点的值），则需要从该节点开始从底向上进行堆化（就是需要不断调整交换位置，将新插入的节点与其父节点的值交换），就这样一直操作，直到越过根节点或遇到无需交换的节点时结束。

如下图1，2中的所示，新插入元素7，但其大于其父节点的值5，所以先进行一步交换，然后再把7与其父节点6进行比较，仍大于继续交换，最后判断7是否大于其父节点的值9，很明显不大于，则最后不交换7与9的值。

图1

图2

3.3、堆顶元素出堆

    堆顶元素是完全二叉树的根节点，也就是列表首元素，若直接从列表中删除它，那么会导致列表中所有结点的索引都会发生变化，故会有以下的操作：

首先，交换堆顶元素与堆底元素，也就是根节点与最右边的叶子节点。

然后，交换完成后，将堆底元素从列表中删除，实际就是把原来的堆顶元素给删除了。

最后，从根节点开始，由顶到底进行堆化操作。

注意，这里的堆化操作是由顶至底进行的，在调整时，需要把根节点与最大的子节点进行交换，这样便会找到除了原本的头节点以外最大的元素，也就是次大元素，如此循环往复，直到越过叶子节点或遇到无需交换的节点为止。

如图3，4所示，要删除原来的堆顶元素9，故需要先将堆顶元素9与堆底元素5交换位置，然后直接将新的堆底元素删除；接下来就需要堆化操作：将元素5与其最大的子节点8交换，再把元素5与其当前的最大的子节点7进行交换，再把元素5与其最大的子节点6进行交换，这样便交换完成，元素6成为元素3和5的父节点，整体满足了大顶堆。

图3

图4

3.4代码

class MaxHeap:
    def __init__(self,num:list[int]):
        # 将列表中的元素添加到堆中
        self.max_heap = num
    def left(self,i:int)->int:
        """获取索引i节点的左子节点"""
        return 2 * i + 1

    def right(self,i:int)->int:
        """获取右子节点的索引"""
        return 2 * i + 2

    def parent(self,i:int)->int:
        """获取节点i的父亲节点索引"""
        return (i - 1) // 2 # 向下取整

    def peek(self)->int:
        """获取堆顶元素"""
        return self.max_heap[0]

    def size(self)->int:
        """堆的大小"""
        return len(self.max_heap)

    def push(self,val:int):
        """元素入堆"""
        self.max_heap.append(val)
        # 从底至顶堆化
        self.sift_up(self.size() - 1)

    def swap(self,i:int,j:int):
        """交换元素"""
        self.max_heap[i],self.max_heap[j] = self.max_heap[j],self.max_heap[i]

    def sift_up(self,i:int):
        """从节点i开始，从底至顶堆化"""
        while True:
            # i节点的父节点
            p = self.parent(i)
            if self.max_heap[i] <= self.max_heap[p] or p < 0:
                break
            self.swap(i,p)
            # 循环向上堆化
            i = p
    
    def pop(self)->int:
        """堆顶元素出堆"""
        if self.size() == 0:
            raise IndexError("堆为空")
        # 交换堆顶节点与堆底节点
        self.swap(0,self.size()-1)
        # 删除节点
        val = self.max_heap.pop()
        self.sift_down(0)
        # 返回堆顶元素
        return val
    def sift_down(self,i:int):
        while True:
            l, r, ma = self.left(i),self.right(i),i
            if l < self.size() and self.max_heap[l] > self.max_heap[ma]:
                ma = l
            if r < self.size() and self.max_heap[r] > self.max_heap[ma]:
                ma = r
            if ma == i:
                break
            # 交换两个节点
            self.swap(i,ma)
            # 循环向下堆化
            i = ma
        

 4、堆的常见应用

• 优先队列通常作为实现优先队列的首选数据结构，其入队和出队操作的时间复杂度均为 O(log⁡ n) ，而建堆操作为 O(n) ，这些操作都非常高效。
• 堆排序给定一组数据，我们可以用它们建立一个堆，然后不断地执行元素出堆操作，从而得到有序数据。然而，我们通常会使用一种更优雅的方式实现堆排序，详见“堆排序”章节
• 获取最大的k个元素这是一个经典的算法问题，同时也是一种典型应用，例如选择热度前 10 的新闻作为微博热搜，选取销量前 10 的商品等。

 二、建堆操作

    在某些情况下，我们希望使用一个列表的所有元素来创建一个堆，这个过程被称为建堆操作。

1、借助入堆操作实现

    先创建一个空堆，然后依次对每一个元素执行入堆操作，即先将元素添加至堆的尾部，再对元素执行从底至顶堆化。且每当一个新的元素入堆，堆的长度就要加1。由于元素的插入是按照从顶到底的方式插入的，因此这种方式是自上而下构建的堆。

若每个元素的入堆操作时间复杂度为O(log n)，那么建堆方法（有n个元素）的时间复杂度就为O(n log n)。

2、通过遍历堆化实现

    这是一种实现更高效的建堆方法，主要分为两步：

首先，将列表中的所有元素原封不动的添加到堆中，此时堆还尚未能满足大根堆或小根堆的性质；

然后，倒序遍历堆（层序遍历的倒序），依次对每个非叶子节点执行从顶至底堆化操作。

补充一下，这里为什么要选择层序遍历的倒序呢？因为使用层序遍历的倒序，并且对所有非叶子节点按照从顶至底的顺序进行堆化，可以保证当前节点之下的子树已经是合法的子堆。

为什么要针对于非叶子节点进行堆化呢，因为叶子节点无子结点，他们天生就是合法的子堆，并且在对非叶子节点堆化时，就已经涉及到堆化操作了，会保证最后是符合堆的结构的。

    def __init__(self,num:list[int]):
        # 将列表中的元素添加到堆中
        self.max_heap = num
        # 按照层序遍历的倒序顺序堆化所有非叶子节点
        for i in range(self.parent((self.size() - 1)),-1,-1):
            self.sift_down(i)

上述代码就是说索引从self.size()-1排序到不包含-1的数，也就是从 self.size()-1排到0，步长为-1，即从父节点向上遍历到根节点一共是self.size()个元素，针对于每个元素都按照从顶到底的方式堆化。

复杂度分析

• 假设完全二叉树的节点数量为 n，则叶节点数量为 (n+1)/2 ，其中 / 为向下整除。因此需要堆化的节点数量为 (n−1)/2 。
• 在从顶至底堆化的过程中，每个节点最多堆化到叶节点，因此最大迭代次数为二叉树高度 log⁡n 。

将上述两者相乘，可得到建堆过程的时间复杂度为O(n log n)。但这个估算结果并不准确，因为我们没有考虑到二叉树底层节点数量远多于顶层节点的性质。

    接下来我们来进行更为准确的计算。为了降低计算难度，假设给定一个节点数量为 n、高度为 ℎ 的“完美二叉树”，该假设不会影响计算结果的正确性。

 如图 8-5 所示，节点“从顶至底堆化”的最大迭代次数等于该节点到叶节点的距离，而该距离正是“节点高度”。因此，我们可以对各层的“节点数量 × 节点高度”求和，得到所有节点的堆化迭代次数的总和。

三、Top-k问题

Question:给定一个长度为n的无序数组nums，请返回数组中最大的k个元素。

    对于该问题，可以先介绍比较直接的思路解法，再介绍比较更高的堆的解法。

解法1：遍历/迭代

    类似于选择排序的思路：进行k轮遍历，每轮找到当前nums中剩余的未排序的最大的元素，时间复杂度为O(n*k)，显然，当k<<n时，还比较使用，但当k无限接近于n的时候，时间复杂度与趋近于O(n^2)，非常耗时。

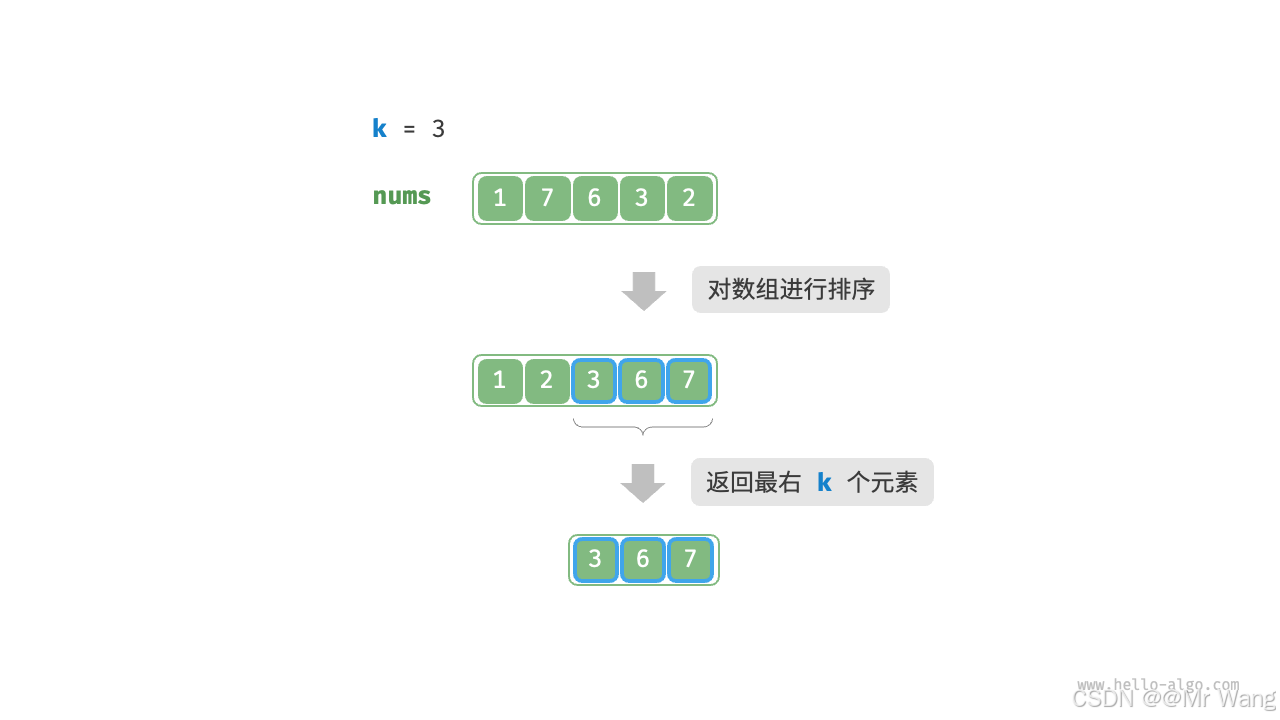
 解法2：排序

    可以先对数组排序，然后根据排序的顺序截取k个元素即可，但时间复杂度为O(n log n)，显然这种做法有点冗余了，我们并不需要一直求解到第n大的元素，求解到第k大的元素即可。故我们只需要找出最大的k个元素即可（以k为限制条件），而不需要排序其他的元素。

解法3：基于堆的解法

    因为是需要返回前k个大的元素，所以我们使用一个小根堆，保证其堆顶的元素最小；然后将数组的前k个元素分别入堆；接着从第k+1个元素开始，若当前元素大于堆顶元素，将堆顶元素出堆，将当前元素入堆；遍历完所有元素后，堆中保存的就是最大的k个元素。

import heapq

def top_k_heap(nums:list[int],k:int)->list[int]:
    """基于小顶堆查找数组中的最大的k个元素"""
    heap = []
    for i in range(k):
        heapq.heappush(heap,nums[i])
    for i in range(k,len(nums)):
        if nums[i]>heap[0]:
            heapq.heappop(heap)
            heapq.heappush(heap,nums[i])
    return heap

num = [1,7,6,3,2,5]
l = top_k_heap(num,4)
print(f"前k个最大的元素为{l}") # output:前k个最大的元素为[3, 5, 6, 7]

总共执行了n轮入堆和出堆，堆的最大长度为k，因此时间复杂度为O(n log k)，该方法的效率很高，当k较小时，时间复杂度趋于O(n)；当k很大时，时间复杂度不会超过O(n log n)。

四、交换两个元素值

方法1

    在Python中，可以通过元组解包或多重赋值来交换两个元素的值。

# 方法1
a,b = 10,1
a,b = b,a

方法2

    添加中间变量，这也是在一些其他编程语言中常会用到的思想。

a,b = 10,1
tmp = a
a = b
b = tmp

方法3

    不使用中间变量，或者是Python所自带的多重赋值，那么使用算术运算和逻辑运算也同样可以实现两个元素值的交换。

 3.1算术运算

    算术运算就比如一些可以先是正运算，再是逆运算的运算规则进行求解。

3.1.1加减法

# 加减法
a,b = 10,1
a = a + b
b = a - b
a = a - b

3.1.2乘除法

# 乘除法
a,b = 10,1
a = a * b
b = a / b
a = a / b

方法4

    使用逻辑运算符号异或

a,b = 10,1
a = a ^ b
b = a ^ b
a = a ^ b