目录
- 一、排序算法 Sorting algorithms
- 二、数据结构 Data Structures
- 三、动态规划 Dynamic Programming
- 四、最小生成树Minimum Spanning Tree
- 五、最短路径问题 Shortest Path
- 六、Maximum Flow 最大流
- 七、字符串匹配算法
- 计算相关
- 推荐学习网站
一、排序算法 Sorting algorithms
- 插入排序 (Insertion sort)
- 归并排序 (Merge sort)
- 堆排序 Heap sort
- 快速排序 Quick sort
插入排序 (Insertion sort)
第n个元素依次比较前n-1个已排序好的数组元素直到插入相应位置
平均时间复杂度:O(n²)
空间复杂度:O(1)

def insertion_sort(seq):
for j in range(1, len(seq)):
key = seq[j]
i = j - 1
while i >= 0 and seq[i] > key:
seq[i + 1] = seq[i]
i = i - 1
seq[i + 1] = key
return seq归并排序 (Merge sort)
分治法;连续二等分后子序列进行比较排序到一个新数组之中,再两两合并
时间复杂度:O(nlogn)
最坏空间复杂度:O(n)
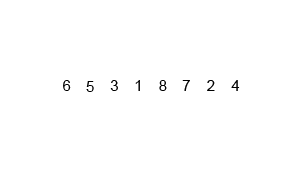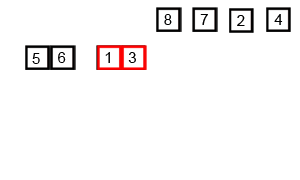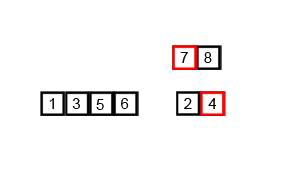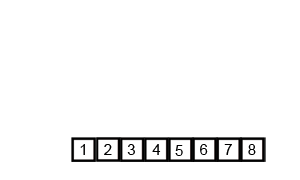
def merge_sort(arr):
if len(arr) == 1:
return arr
mid = len(arr) // 2
left = arr[:mid]
right = arr[mid:]
return marge(merge_sort(left), merge_sort(right))
def marge(left, right):
result = []
# 两个数列都有值
while len(left) > 0 and len(right) > 0:
# 左右两个数列第一个最小放前面
if left[0] <= right[0]:
result.append(left.pop(0))
else:
result.append(right.pop(0))
# 只有一个数列中还有值,直接添加
result += left
result += right
return result
//或者用 指针
def merge(left,right):
res = []
i,j =0, 0
while i<len(left_half) and j<len(right_half):
if left_half[i] >= right_half[j]:
res.append(right_half[j])
j+=1
else:
res.append(left_half[i])
i+=1
if i==len(left_half) and j<len(right_half):
res.extend(right_half[j:])
if i<len(left_half) and j==len(right_half):
res.extend(left_half[i:])
return res堆排序 Heap sort
堆是一种完全二叉树 构建大顶堆maxheap -> 交换根节点和末节点 -> 堆顶heapify再次形成大顶堆
时间复杂度:O(nlogn)

#由结点i开始向下max-heapify
def heapify(arr, n, i):
largest = i
left = 2*i+1
right = 2*i+2
if left<n and arr[left]>arr[largest]:
largest= left
if right<n and arr[right]>arr[largest]:
largest= right
if largest != i:
arr[largest], arr[i]= arr[i],arr[largest]
# Heapify the root.
heapify(arr, n, largest)
#构建max heap (根节点大于子节点)
def maxheap(arr, n):
for i in range(n//2 - 1, -1, -1):
heapify(arr, n, i)
#堆排序
def heapSort(arr):
n = len(arr)
maxheap(arr, n)
for i in range(n-1, 0, -1):
arr[i], arr[0] = arr[0], arr[i]
heapify(arr, i, 0)
快速排序 Quick Sort
选出一个基准值(pivot),将数组分为两份:一份小于基准值,一份大于基准值,递归进行
平均时间复杂度:O(nlogn)
空间复杂度O(logn)

#方法一:一次遍历
def partition(arr, left, right):
pivot = arr[right]
i = left
for j in range(left, right):
if arr[j] <= pivot:
arr[j], arr[i] = arr[i], arr[j]
i += 1
arr[i], arr[right] = arr[right], arr[i]
return i
def quickSort(arr, left, right):
if left < right:
p = partition(arr, left, right)
quickSort(arr, left, p-1)
quickSort(arr, p+1, right)
#方法二:迭代循环 (见参考)
def quick_sort_standord(array,low,high):
''' realize from book "data struct" of author 严蔚敏
'''
if low < high:
key_index = partion(array,low,high)
quick_sort_standord(array,low,key_index)
quick_sort_standord(array,key_index+1,high)
def partion(array,low,high):
key = array[low]
while low < high:
while low < high and array[high] >= key:
high -= 1
if low < high:
array[low] = array[high]
while low < high and array[low] < key:
low += 1
if low < high:
array[high] = array[low]
array[low] = key
return low二、数据结构 Data Structures
- 栈(Stack)
- 队列(Queue)
- 数组(Array)
- 链表(Linked List)
- 树(Tree)
- 图(Graph)
- 堆(Heap)
- 散列表(Hash table)
1. 链表 Linked List
- 单向(循环)链表
- 双向链表
2. 栈(Stack)和队列(Queue)
LIFO后进先出 和FIFO先进先出
'''栈Stack 进append() 出pop()'''
lst = []
lst.append("1")
lst.append("2")
ret = lst.pop() # 2
'''队列 进: put() 出: get()'''
import queue
q = queue.Queue() # 创建队列
q.put("1")
q.put("2")
print(q.get()) # 1-
python的双向队列(deque) double ended queue
相比于list实现的队列,deque实现拥有更低的时间和空间复杂度。list实现在出队(pop)和插入(insert)时的空间复杂度大约为O(n),deque在出队(pop)和入队(append)时的时间复杂度是O(1)。deque既可以表示队列 又可以表示栈。deque在python标准库collections中。

from collections import deque
'''deque支持in操作符'''
q = collections.deque([1, 2, 3, 4])
print(5 in q) # False
print(1 in q) # True
'''deque里边的形式是列表形式'''
#顺逆时针旋转
# 顺时针
q = collections.deque([1, 2, 3, 4])
q.rotate(1)
print(q) # [4, 1, 2, 3]
q.rotate(1)
print(q) # [3, 4, 1, 2]
# 逆时针
q = collections.deque([1, 2, 3, 4])
q.rotate(-1)
print(q) # [2, 3, 4, 1]
q.rotate(-1)
print(q) # [3, 4, 1, 2]4. 哈希表(散列表) Hash Table
d = {key1 : value1, key2 : value2 }5. 树类数据结构
- 二叉搜索树 binary search Tree:左子树值 < 根节点值 < 右子树值
- AVL平衡二叉搜索树(要平衡先搜索):任何节点的左和右子树高度最多相差1(严格平衡)
- 红黑树:二叉搜索树,最长路径不大于两倍的最短路径的长度(近似平衡)
- 多路查找树:每一个节点的儿子可以多于两个,且每一个节点可以存储多个元素
5.1 二叉查找树 Binary Search Tree
满足条件:所有的 左子树值 < 根节点值 < 右子树值
- 前序遍历(preorder): 根节点 -> 左子树 -> 右子树
- 中序遍历(inorder): 左子树 -> 根节点 -> 右子树
- 后序遍历(postorder): 左子树 -> 右子树 -> 根节点
二叉搜索树的删除:如果左右子树都存在,找右子树最小值代替删除节点。或者左子树最大值。
class Node:
def __init__(self, key):
self.left = None
self.right = None
self.key = key
def Insert(self, key):
if key>self.key:
if self.right:
self.right.Insert(key)
else:
self.right= Node(key)
else:
if self.left:
self.left.Insert(key)
else:
self.left= Node(key)
# Inorder traversal
# Left -> Root -> Right
def InorderTraversal(self, root):
res = []
if root.left:
res+=root.InorderTraversal(root.left)
res.append(root.key)
if root.right:
res+=root.InorderTraversal(root.right)
return res
def Minimum(self,node):
while node.left:
node=node.left
minimum=node
return minimum
#删除两种实现:第一种可处理根节点的删除
def Delete(self, root, key):
position=None
while root.key !=key:
pre=root
if root.key>key:
root=root.left
position="left"
else:
root=root.right
position="right"
if not root:
return
if root.right and root.left:
nex=self.Minimum(root.right)
self.Delete(root, nex.key)
root.key=nex.key
elif root.right:
nex=root.right
if not position:
root.key=nex.key
root.left=nex.left
root.right=nex.right
elif root.left:
nex=root.left
if not position:
root.key=nex.key
root.left=nex.left
root.right=nex.right
else:
nex=None
if position=="left":
pre.left=nex
if position =="right":
pre.right=nex
if not (position or nex):
root.key=None
#第二种迭代 :
def _Delete(self, root, key):
if not root:
print('not find key')
elif key < root.key:
root.left = self._Delete(root.left, key)
elif key > root.key:
root.right = self._Delete(root.right, key)
elif root.left and root.right:
right_min = self.Minimum(root.right)
root.key = right_min.key
root.right = self._Delete(root.right, right_min.key)
elif root.left:
root = root.left
elif root.right:
root = root.right
else:
root = None
return root
5.2 AVL 自平衡二叉查找树 Balanced Tree
每个节点的左子树和右子树的高度差为{-1,0,1}
5.3 红黑树 Red-Black Tree
红黑树是一种含有红黑结点并能自平衡的二叉查找树。其红黑规则:
- 节点不是黑色,就是红色(非黑即红)
- 根节点为黑色
- 叶子节点为黑色(叶节点是指末梢的空节点
Nil或Null) - 每个红色节点的两个子节点一定都是黑色(根到叶子的所有路径,不可能存在两个连续的红色节点)
- 每个节点到叶子节点的所有路径,都包含相同数目的黑色节点(相同的黑色高度)

红黑树自平衡的三种操作:
- 左旋:以某个结点作为支点(旋转结点),其右子结点变为旋转结点的父结点,右子结点的左子结点变为旋转结点的右子结点,左子结点保持不变。
- 右旋:以某个结点作为支点(旋转结点),其左子结点变为旋转结点的父结点,左子结点的右子结点变为旋转结点的左子结点,右子结点保持不变。
- 变色:结点的颜色由红变黑或由黑变红。
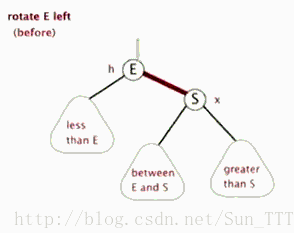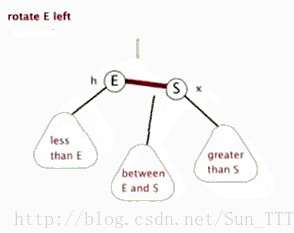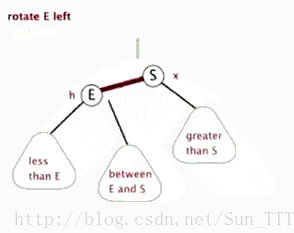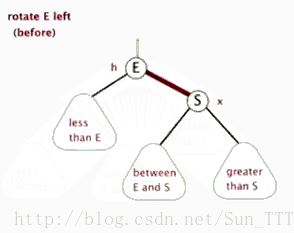
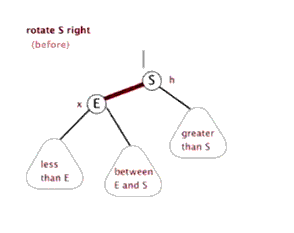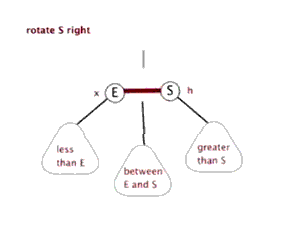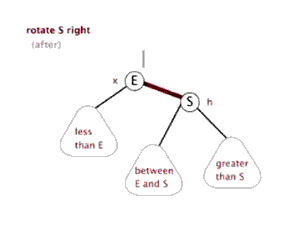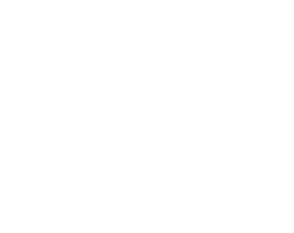
红黑树的操作
查找:和二叉查找树一样
插入:插入节点选红色,可忽略一些自平衡操作。插入情况:
当插入节点的父节点为黑节点,直接插入。
当插入结点的父节点为红节点时,如果
- 叔叔结点存在并且为红结点,则变色。再将祖父节点作为插入节点进行自平衡
- 叔叔结点不存在或为黑结点,先旋转父节点,变色,再旋转祖父节点。
删除:情景比较多。总的来说还是不断旋转和变色
红黑树的复杂度
从操作复杂度看,AVL树和红黑树查找、插入、删除都是O(logn)
进一步考虑:
1)查找:红黑树牺牲了严格平衡,但是保证了最长路径不大于最短路径的两倍,所以查找某个节点也可以保证O(logn);但是对于大规模数据的查找,AVL树的严格平衡显然使得查询效率更高(查找上:AVL树胜)
2)插入:如果是插入一个节点引起的不平衡,AVL树和红黑树都是最多通过2次旋转来修正,两者均是O(1)。如果新节点的父结点为黑色,那么插入一个红点将不会影响红黑树的平衡。但红黑树这种黑父的情况比较常见,从而使红黑树需要旋转的概率0比AVL树小
3)删除:如果删除某个节点引起了不平衡,AVL树需要维护被删除节点到根节点的整条路径上所有节点的平衡性,需要O(logn);而红黑树最多只需3次旋转,只需要O(1)
所以说,在大规模数据插入或者删除时,AVL树的效率不如红黑树(插入和删除上:红黑树胜)
5.4 多路查找树
2-3树、2-3-4树、B树、B+树
5.4.1 B树
一颗m阶B树是一颗空树或者是符合一系列条件的m叉树
6. 图论 Graph Theory
- 有向图/无向图
- BFS/DFS
7. 堆(Heap)
堆通常是一个可以被看做一棵完全二叉树的数组对象。堆满足下列性质:
- 堆中某个节点的值总是不大于或不小于其父节点的值。
- 堆总是一棵完全二叉树。
三、动态规划 Dynamic Programming
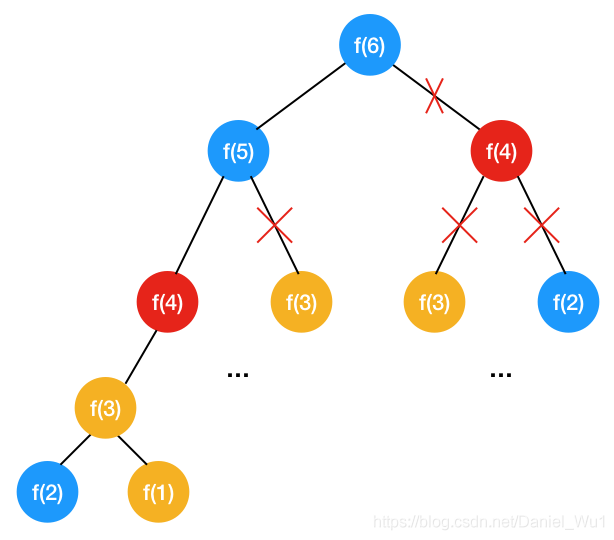
D&C分而治之 Bottom-up自底向上解法:先求解更小的子问题
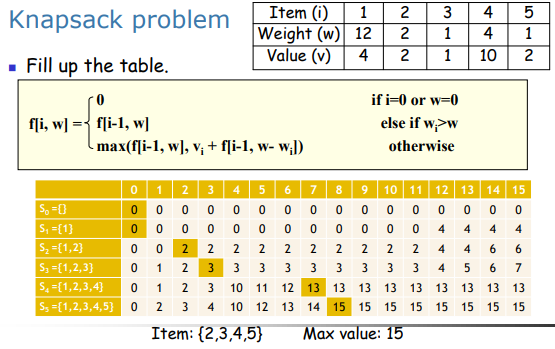
1. 背包问题
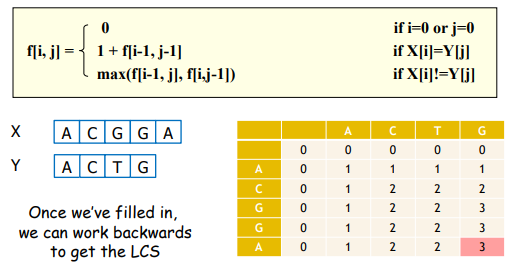
2. Longest Common Subsequence (LCS) 最长公共子序
#示例:斐波那契数列
def DP_Fibonacci(n):
F = [1 for i in range(n+1)]
for i in range(2,n+1):
F[i] = F[i-1] + F[i-2]
return F[n]
#0-1背包问题 时间复杂度O(nW)
#二维
def knapsack(W, weight, value, n):
f = [[None]*(W+1) for x in range(n + 1)]
for i in range(n+1):
for w in range(W+1):
if i==0 or w==0:
f[i][w]=0
elif weight[i-1]>w:
f[i][w]=f[i-1][w]
else:
f[i][w]=max(f[i-1][w-weight[i-1]]+value[i-1],f[i-1][w])
#打印物品列表
v=f[n][W]
w=W
res=[]
for i in range(n,0,-1):
if v-value[i-1]==f[i-1][w-weight[i-1]]:
res.append(i)
v-=value[i-1]
w-=weight[i-1]
print(res[::-1])
return f[n][W]
#一维优化
n, v = map(int, input().split())
goods = []
for i in range(n):
goods.append([int(i) for i in input().split()])
dp = [0 for i in range(v+1)]
for i in range(n):
for j in range(v,-1,-1): # 从后往前
if j >= goods[i][0]:
dp[j] = max(dp[j], dp[j-goods[i][0]] + goods[i][1])
print(dp[-1])
#最长子序列问题
四、最小生成树Minimum Spanning Tree
1. 概述
最小生成树(MST):在包含 n个顶点的带权无向连通图中, 找出(n-1)条边的最小耗费生成树(权值最小)
带权图:边赋以权值的图称为网或带权图,带权图的生成树也是带权的,生成树T各边的权值总和称为该树的权。
最小生成树的性质:假设G=(V,E)是一个连通网,U是顶点V的一个非空子集。若(u,v)是一条具有最小权值的边,其中u∈U,v∈V-U,则必存在一棵包含边(u,v)的最小生成树。
完成构造网的最小生成树必须解决下面两个问题:
(1)尽可能选取权值小的边,但不能构成回路;
(2)选取n-1条恰当的边以连通n个顶点;
prim算法适合稠密图,kruskal算法适合简单图
2. Kruskal's algorithm 克鲁斯卡尔算法
不成环,(全局)依次取权值最小。

3. Prim's algorithm 普里姆算法
普利姆算法步骤:
- 选取权值最小边的其中一个顶点作为起始点。
- 找到离已选择(当前)顶点权值最小的边,并记录该顶点为已选择。
- 重复第二步,直到找到所有顶点,就找到了图的最小生成树。
五、最短路径问题 Shortest Path
最短路径问题可分为两方面:
- 图中一个点到其余各点的最短路径
- 图中每对点之间到最短路径
1. Dijkstra's Algorithm 狄克斯特拉算法
基于贪心的单源最短路算法(即指定一个点(源点)到其余各个顶点的最短路径),其要求图中的边全部非负

2. Bellman-Ford Algorithm贝尔曼-福特算法
贝尔曼-福特算法(Bellman-Ford)是求解单源最短路径问题的一种算法。它的原理是对图进行V-1次松弛操作,得到所有可能的最短路径。其优于Dijkstra算法的方面是边的权值可以为负数、实现简单,缺点是时间复杂度过高,高达O(VE).
3. 其他算法
- Floyd弗洛伊德算法:基于动态规划的多源最短路
六、Maximum Flow 最大流
1. 流网络
G=(V,E)是一个有向图,其中每条边(u,v)有一个非负的容量值c(u,v),而且如果E中包含一条边(u,v),那么图中就不存在它的反向边。在流网络中有两个特殊的结点,源结点s和汇点t。
下面给出流网络的形式化定义。令G=(V,E)为一个流网络,其容量函数为c,设s我为网络的源点,t为汇点。G中的流是一个实值函数f,满足以下两条性质:
1. 容量限制(capacity contraint):对于所有的结点u,v,要求
2. 流量守恒(flow conservation):对于所有的非源点和汇点的结点u,要求:
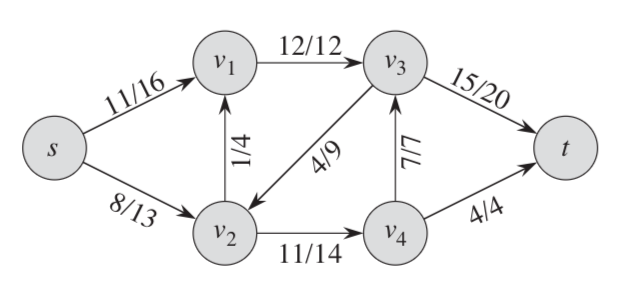
下图是一个流网络的示例图,帮助大家理解,其中的“/”只是分隔符而不是运算符,“/”前代表的是流的值,后面的数值则是该条边的容量(capacity):
2. Ford-Fulkerson Algorithm
每次随机选一个Augmenting edge,取残差网络中path最小flow 加到原图,直到没有路径可选
2.1 残存网络(residual network)
假定有一个流网络G=(V, E),其源点为s,汇点为t,f 为G中的一个流。对即诶点对u,v,定义残存容量(residual capacity),存在:
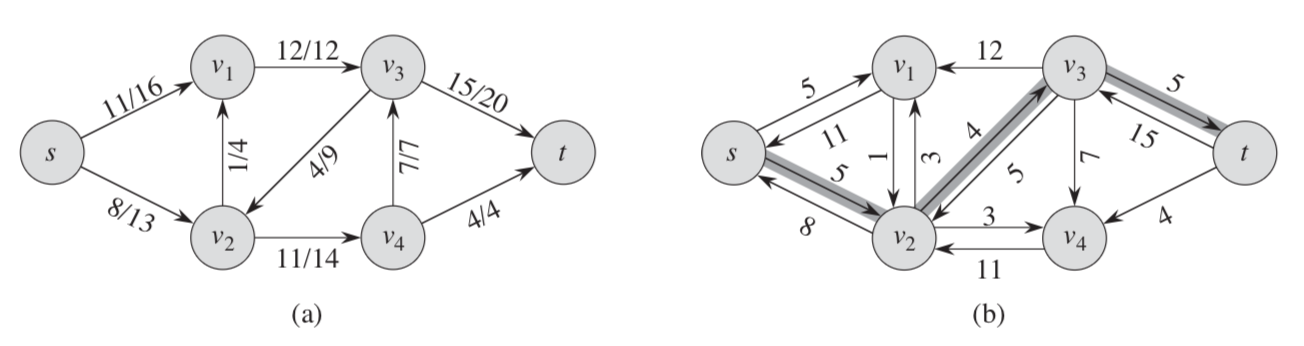
残存网络可能包含图G中不存在的边,残存网络中的反向边允许算法将已经发送出来的流量发送回去。如下图,图a是一个流网络,b是a对应的残存网络
2. 增广路径(augmenting paths)
给定流网络G和流f,增广路径p是残存网络中一条从源结点s到汇点t的简单路径。
3. 流网络的切割s-t cut(cuts of networks)
流网络G中的一个切割(S,T)将结点集合V划分为S和T=V-S两个集合,使得,
。若f 是一个流,则定义横跨切割(S,T)的净流量f(S,T)如下:
切割(S,T)的容量是:
一个网络的最小切割是整个网络中容量最小的切割。
3.1 最大流最小切割定理 Maximum Flow Minimum Cut theorem
设f为流网络G=(V,E)中的一个流,该流网络的源结点为s,汇点为t,则下面的条件是等价的:
1. f是G的一个最大流。
2. 残存网络不包含任何增广路径
3. |f|=c(S,T),其中(S,T)是流网络G的某个切割。
4. Ford-Fulkerson伪代码
计算复杂度O(Cm) , C 是最大流
七、字符串匹配算法

BF算法 Brute Force 暴力算法 (Naïve algorithm)
即穷举法,时间复杂度是 O(n*m) ,其中m为匹配串长度 ,n为主串长度
RK 算法 Rabin-Karp
通过哈希算法对主串中的 n-m+1 个子串分别求哈希值,然后逐个与模式串的哈希值比较大小
KMP 算法 Knuth-Morris-Pratt
- 寻找已匹配字串子序列的最大相同前后缀
--为此需要一个数组先遍历一次主串去存储所有位置的最长前后缀 - 从最大公共前后缀后一位继续与主串匹配
时间复杂度: O(n+m) 长度为n,模式为m
#最长回文前缀
def LongestPrefixPalindrome(self, s: str) -> str:
'''KMP Algorithm'''
'''Find longest prefix-suffix common string'''
common=[0]*len(s)
j=0
for i in range(1,len(s)):
while j>0 and s[i]!=s[j]:
j=common[j-1]
if s[i]==s[j]:
j+=1
common[i]=j
'''Match'''
best=0
for i in range(len(s)-1,-1,-1):
while best>0 and s[i]!=s[best]:
best=common[best-1]
if s[i]==s[best]:
best+=1
return s[:best]BM算法(Boyer-Moore)滑动算法
时间复杂度: O(n/m) n:主串长度 m:模式串长度
Trie 字典树
构建Trie树时间复杂度是 O(n)(n是Trie树中所有元素的个数)
查询Trie树时间复杂度是 O(k)(k 表示要查找的字符串的长度)
Trie树专门处理字符串匹配的数据结构,用来解决在一组字符串集合中快速查找某个字符串的问题
Trie 树的本质,就是利用字符串之间的公共前缀,将重复的前缀合并在一起

构造Trie树:利用数组(每个节点是字符值+下一字符的索引)
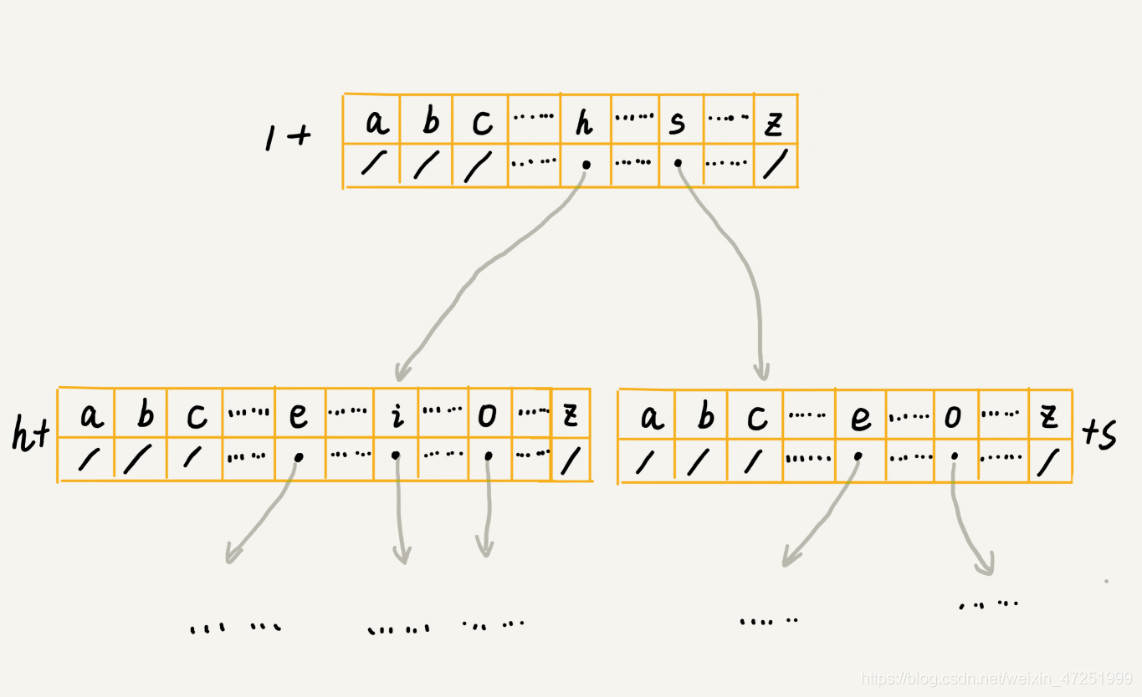
匹配算法
- 单模式串匹配算法,是在一个模式串和一个主串之间进行匹配,也就是说,在一个主串中查找一个模式串。
- 多模式串匹配算法,就是在多个模式串和一个主串之间做匹配,也就是说,在一个主串中查找多个模式串。(AC自动机)
AC自动机 Aho-Corasick automaton
AC自动机基于KMP算法和Trie树。
应用场景:给出n个单词,再给出一段包含m个字符的文章,找出有多少个单词在文章里出现过
步骤:
- 先要构建一个敏感词字典树Trie树
- 只需要遍历一遍文本就能找出所有的敏感词
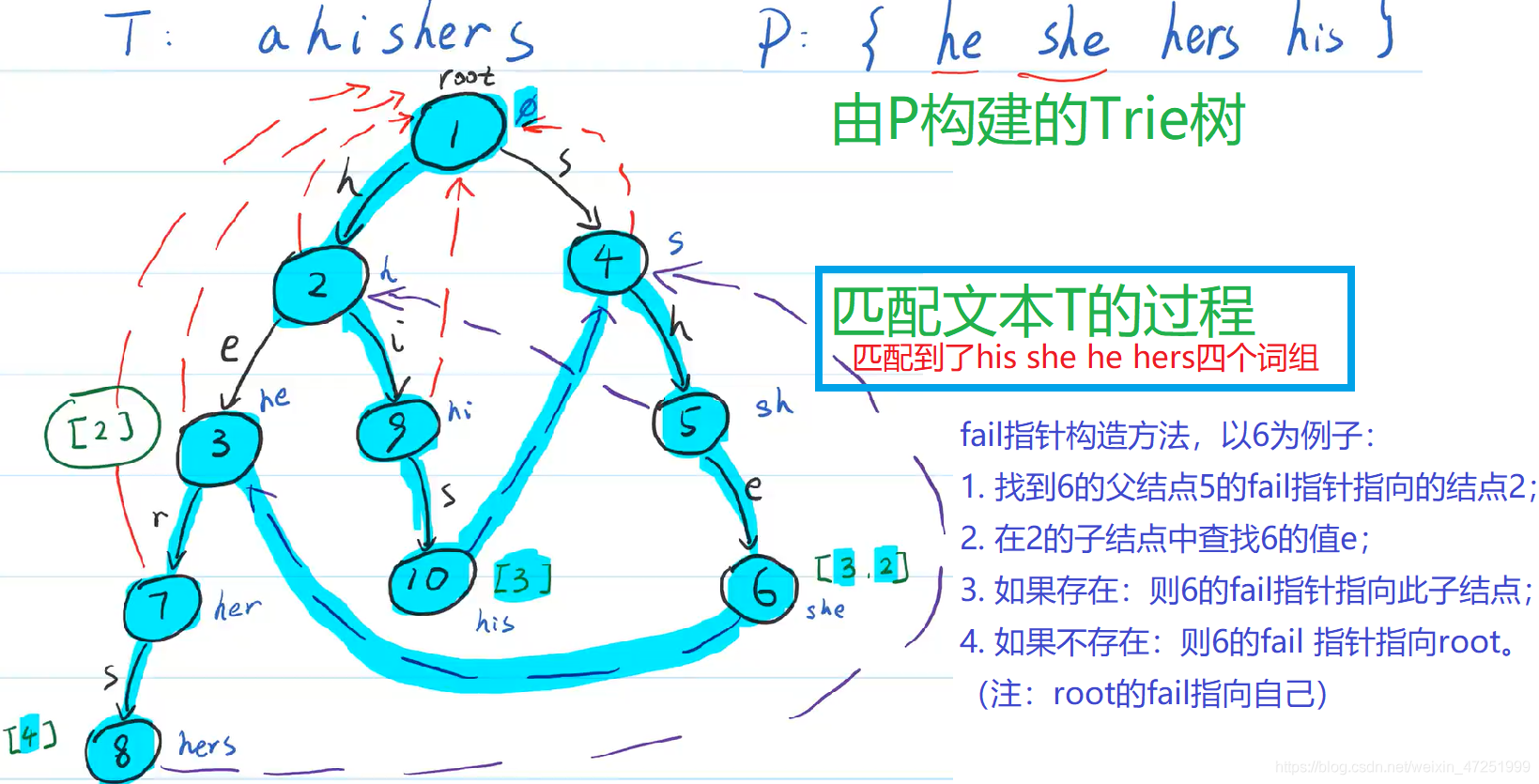
匹配的时间复杂度是 O(n*len)。(n字符数量,len是Trie的高度,即字符串长度)因为敏感词并不会很长,所以实际情况下,近似于 O(n),所以 AC 自动机做敏感词过滤,性能非常高。
计算相关
0. Recurrence
A recurrence is an equation or inequality that describes a function in terms of its value on smaller inputs.

Solving recurrence
- Substitution method: Guess a bound + Mathematic induction
- Recursion-tree method: covert the recurrence into a tree
- Master method
1. The Master Method 主方法
数学上分析递归算法计算复杂度的常用方式

而对应这个问题描述,相应的算法复杂度结果如下:

举例子:
- 归并排序: a=2,b=2,d=1对应第一种,结果是O(nlogn)。
- 二分查找: a=1,b=2,d=0对应第一种,结果是O(logn)。
- naive的递归整数乘法: a=4,b=2,d=1对应第三种,结果是O(n^{2})
2. Number Theory数论
2.1 Divisibility and divisors
d | a 的意义:d divides a, 当 a = kd,k是整数,也说a是d的 multiple, d是a的因子
2.2 Prime (质数/素数) and composite numbers
Division theorem:
对于任意整数a和正整数n,存在唯一的整数 q 和 r, such that 0≤r<n 并且 a = qn + r 。
也就是说 对于每个数,都是 两个数的乘积 加上一个数

2.3 Common Divisors and Greatest Common Divisors (GCD) 公约数和最大公约数
Relatively Prime Integers: 整数a和b互质,如果它们公约数只有 1。 gcd(a,b)=1
Unique factorization:合数的唯一分解。p是质数,e是正整数
![]()
如果有两个合数则他们的GCD为: 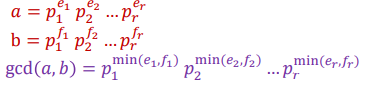
2.4 GCD recursion theorem
对任何非负整数a和正整数b,有
![]()
证明:只需证明gcd(b, a mod b) | gcd(a, b) 和 gcd(a, b) | gcd(b, a mod b)两种情况
2.5 Euclid’s Algorithm 欧几里得算法
对任何非负整数a和b

2.6 Extended Euclid’s Algorithm
返回形式: d = gcd(a, b) = ax + by
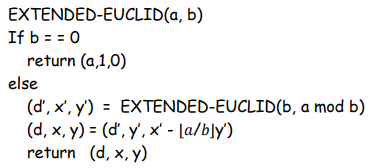

先从上向下遍历a, b, floor(a/b)表,再从下向上遍历d,x,y表。
2.7 Modular Arithmetic 模算术

比如说:![]()
因此a,b同余n写作![]()
2.7.1 Modular Multiplicative Inverse 模乘逆元
- 模乘逆元定义:满足 ax ≡ 1(mod n),称x为a模乘逆元. x也写作 a^-1 mod n
- 模乘逆元存在当且仅当a和n互质 (i.e. gcd(a, n) = 1)
Multiplicative group of integers modulo n 模n的整数乘法群:

如何获得模n的整数乘法群?
考虑𝑎𝑥 + 𝑛𝑦 = 1的Extended Euclid’s Algorithm算法, 比如:
- Evaluate 17^(-1) mod 91
- gcd(17,91) = gcd(91, 17) = 1 = 91 * 3 + 17*(-16) 这步用EEA计算获得
- We have 17^(-1) ≡ -16 ≡ 75 (mod 91)
2.7.2 Euler’s totient function 欧拉函数
基于模n的整数乘法群:

实例:
2.7.3 Euler’s theorem
对于任何大于1的整数n:
![]()
练习题:

2.7.4 Fermat’s Theorem
对任意素数p,
![]()
也就是说对于素数p有![]()
2.8 Modular Exponentiation 模幂运算
模幂运算是对给定的整数p、n、a,计算
这个运算在密码学中应用极为普遍,RSA、ElGamal、DH交换等重要密码方案中都涉及模幂运算
2.8.1 Repeated squaring 重复乘方

由左至右遍历表b,c,d
2.9 RSA public-key cryptography
RSA cryptosystem
生成公钥和私钥步骤

加密解密信息

3. NP问题
- P问题:能够在多项式时间内被解决的问题
- NP问题:能够在多项式时间内使用非确定性算法(non-deterministic)被解决的问题
简单来说,必须以非常规方法才能在多项式时间内解决的问题,就叫做NP问题(通过verify)
- NP-complete NP完全问题:只能通过非确定性算法,在多项式时间内解决的问题,叫做NP完全问题
一般来说,非常规方法既可以解决P问题,也可以解决NP问题,所以,只有用非常规方法才能解决的问题,才能叫做NP完全问题
- NP-Hard问题:和NP问题一样困难,或者更加困难的问题
3.1 Decision problem & Optimisation problem
- Decision problem输出是yes或no,而Optimisation problem求最大化或最小化。
- Optimisation problem可以添加参数k被转换为Decision problem,求是否结果最大为k或最小为k
- 如果Decision problem是困难的,则它对应的Optimisation problem也是困难的
3.2 案例
P问题:
- MST problem
- Single-source-shortest-paths problem
NP问题:
- Hamiltonian circuit problem
- 0/1 Knapsack problem
- Circuit-SAT
NP完全问题:
Cook-Levin Theorem证明了3-SAT是NP完全问题
- CNF-SAT and 3-SAT (conjunctive normal form satisfiability problem)
- 3-Coloring
- K-Clique
- Vertex Cover
3.3 Polynomial-time reduction 多项式时间归约
在计算复杂性理论中,多项式时间归约是指假设已有解决一个问题的子程序,利用它在多项式时间内(不考虑子程序运行所用时间)解决另一个问题的归约方法。
如果问题A和问题B满足以下两条性质,那么问题A可以在多项式时间归约到问题B。
- 问题A可以通过多项式时间的基本运算步骤转换为问题B;
- 问题A多项式次调用求解问题B的算法,且问题B可以在多项式时间内被求解。记为
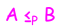
需要注意的是,问题A转换为问题B之后,问题B的运行时间是建立在问题B的输入上。
对于这个定义,可以简单理解为:求解问题B算法需要多项式时间,问题A转换为问题B需要多项式个基本运算加上多项式次调用求解问题B的算法。因此总共需要的时间是:多项式 + 多项式 * 多项式。
因此,如果A不能在多项式时间内求解,那么B也不能在多项式时间内求解
3.4 证明一个问题是NP完全问题
判断⼀个问题是不是NP-Complete有两个步骤:
1. 判断是否NP,就是算法结果的正确性能不能在多项式时间内验证
2. 判断是否NP-hard,要判断NP-hard,我们可以使⽤⼀个叫Reduction的技巧。直观来说,如果你能⽤你的问题的求解器来求解另⼀个已知是NP-hard问题,那么你的问题也是NP-Hard的。
或者 首先找到一个已知的NP完全问题,然后证明这个问题能规约到想要被证明NP完全性的问题。那么就可以说它是一个NP完全问题了。
对于A->B(A规约到B),就是证明A的输入能映射为B的输入,B的输出能映射为A的输出。(注意映射方向)
推荐学习网站
Algorithm Visualizer——算法可视化及代码
参考References
图解排序算法及实现——归并排序 (Merge Sort)_张渊猛的博客-CSDN博客_mergesort
快速排序quick_sort(python的两种实现方式) - 代码王子 - 博客园
快速排序算法图解与PHP实现讲解_weixin_34067102的博客-CSDN博客
Python数据结构————二叉查找树的实现 - 再见紫罗兰 - 博客园
二叉查找树(binary search tree)——python实现_hjj414的博客-CSDN博客
详解动态规划算法_byteshow的博客-CSDN博客_动态规划算法
python的deque(双向)队列详解 - 然终酒肆 - 博客园
个人复习整理,侵删








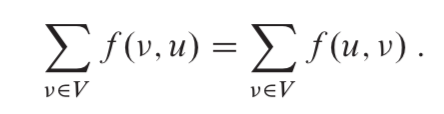
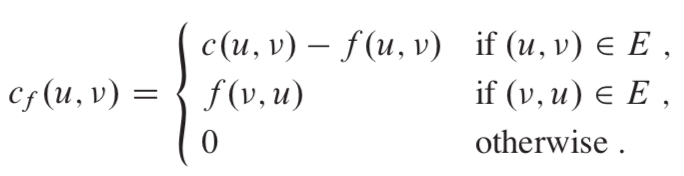
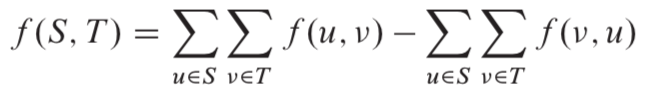
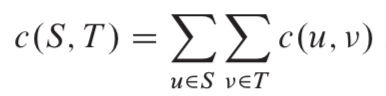
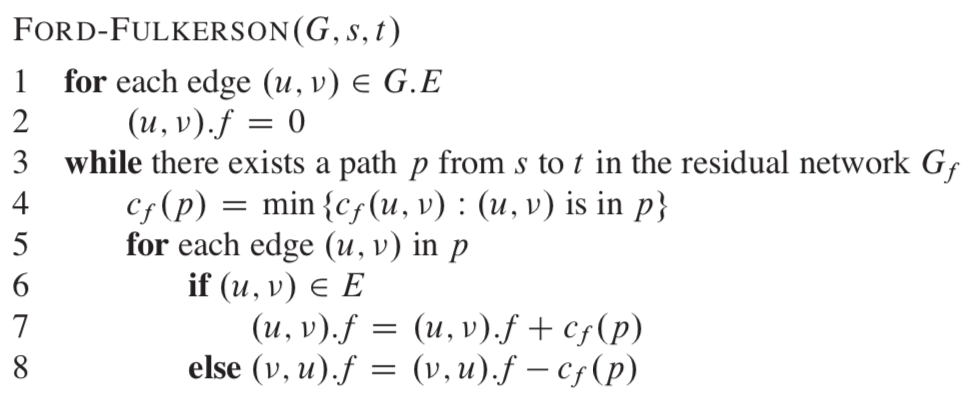















 2277
2277











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








