引言
欢迎来到算法江湖!今天我们将化身两种不同的角色——“质数猎人”与“等差数列侦探”,展开一场智慧与策略的较量。
第一个任务,我们要在数字丛林中寻找相隔最远的质数宝藏,还要确保宝藏之间的路上没有其他质数埋伏;第二个任务,我们要化身侦探,在数列迷宫中用双指针魔法,揪出所有隐藏的等差数列三元组!
这两个问题看似毫无关联,实则都暗藏数学规律与算法设计的精妙博弈。究竟哪种解法更巧妙?哪种思路更高效?让我们拨开迷雾,一探究竟!
正文
一、质数猎人的寻宝挑战(排序+数学)
任务描述
在给定数组中,找到两个质数,它们之间的间隔最大,且这两个质数之间的所有数必须都是非质数。这就像在数字沙漠中寻找两座最远的绿洲,且中途不能有其他水源。
示例:
[2,5,9,11,15] → 选择 2 和 11,间隔为 9,中间的数 9 和 15 都是非质数。
算法策略
-
质数筛选术:
-
快速判断一个数是否为质数(仅能被
1和自身整除),优化方法:只需检查到其平方根。
-
-
排序魔法:
-
将数组排序后,质数的位置一目了然,方便寻找最大间隔。
-
-
双指针扫描:
-
从最左端(最小质数)和最右端(最大质数)开始,向中间收缩,验证中间数是否全为非质数。
-
核心难点:
-
必须确保两个质数之间的所有数都是“荒地”(非质数),否则宝藏会被中途拦截!
#include <stdio.h> // 包含标准输入输出库,用于printf和scanf等函数 #include <stdbool.h> // 包含布尔类型定义(true和false) #include <stdlib.h> // 包含标准库函数,如qsort /** * @brief 判断一个数是否为质数(优化版) * @param num 待判断的整数 * @return true-是质数 false-不是质数 */ bool is_prime(int num) { // 定义一个函数,用于判断一个数是否为质数 if (num <= 1) return false; // 如果数字小于等于1,直接返回false,因为1及以下不是质数 if (num == 2) return true; // 2是唯一的偶质数,直接返回true if (num % 2 == 0) return false;// 如果数字是偶数(除了2),直接返回false // 只需检查到平方根,且跳过偶数因子 for (int i = 3; i * i <= num; i += 2) { // 从3开始,每次加2(只检查奇数) if (num % i == 0) return false; // 如果能被i整除,则不是质数 } return true; // 如果没有被任何数整除,则是质数 } /** * @brief 用于qsort的比较函数(升序排列) * @param a 第一个元素的地址 * @param b 第二个元素的地址 * @return 两元素的差值 */ int compare(const void *a, const void *b) { // 定义比较函数,用于qsort排序 return (*(int*)a - *(int*)b); // 将void指针强制转换为int指针,并返回两个值的差 } /** * @brief 寻找最大质数间隔的核心算法 * @param arr 原始数组 * @param size 数组长度 */ void find_max_prime_gap(int arr[], int size) { // 定义函数,用于寻找最大质数间隔 // 阶段1:数组排序 qsort(arr, size, sizeof(int), compare); // 使用qsort对数组进行升序排序 // 阶段2:质数索引提取(记录排序后的数组索引) int prime_indices[size]; // 定义一个数组,用于存储质数的索引 int prime_count = 0; // 定义一个计数器,用于记录质数的数量 for (int i = 0; i < size; i++) { // 遍历排序后的数组 if (is_prime(arr[i])) { // 如果当前元素是质数 prime_indices[prime_count++] = i; // 将其索引存入prime_indices数组,并计数器加1 } } // 边界条件处理 if (prime_count < 2) { // 如果质数数量小于2,无法形成间隔 printf("Error: Need at least 2 primes\n"); // 输出错误信息 return; // 直接返回 } // 阶段3:寻找最大合法间隔 int max_gap = 0; // 定义变量,用于存储最大间隔 int left = arr[prime_indices[0]], right = arr[prime_indices[0]]; // 初始化左右边界 // 双重循环遍历所有质数对 for (int i = 0; i < prime_count; i++) { // 外层循环,遍历每个质数 for (int j = i + 1; j < prime_count; j++) { // 内层循环,遍历当前质数之后的质数 int start = prime_indices[i]; // 获取左质数在排序数组中的索引 int end = prime_indices[j]; // 获取右质数在排序数组中的索引 int current_gap = arr[end] - arr[start]; // 计算当前质数对的间隔 // 剪枝:如果当前间隔更小则跳过 if (current_gap <= max_gap) continue; // 如果当前间隔不大于已知最大间隔,则跳过 // 关键验证:检查排序数组中两质数之间的元素是否全为非质数 bool all_non_prime = true; // 定义标志变量,假设所有元素都是非质数 for (int k = start + 1; k < end; k++) { // 遍历两质数之间的元素 if (is_prime(arr[k])) { // 如果发现质数 all_non_prime = false; // 标志变量置为false break; // 跳出循环 } } // 更新最大间隔 if (all_non_prime && current_gap > max_gap) { // 如果验证通过且当前间隔更大 max_gap = current_gap; // 更新最大间隔 left = arr[start]; // 更新左边界 right = arr[end]; // 更新右边界 } } } // 结果输出 if (max_gap > 0) { // 如果找到合法的最大间隔 printf("Max prime gap: %d (%d -> %d)\n", max_gap, left, right); // 输出最大间隔及其对应的质数对 } else { // 如果没有找到合法的间隔 printf("No valid prime pairs found\n"); // 输出提示信息 } } int main() { // 主函数 // 测试用例(包含乱序元素) int test_case[] = {5, 2, 9, 15, 11}; // 定义一个测试数组 int size = sizeof(test_case) / sizeof(test_case[0]); // 计算数组长度 // 运行算法 printf("The initial array is: [");// 提示输出原始数组 for (int i = 0; i < size; i++) {// 遍历数组并输出每个元素 // 条件表达式控制逗号格式:首元素无前导逗号 printf(i == 0 ? "%d" : ", %d", test_case[i]); } printf("]\n"); find_max_prime_gap(test_case, size); // 调用函数,寻找最大质数间隔 return 0; // 程序正常结束 }输出结果;
-

二、等差数列侦探的破案之旅(双指针+数学)
任务描述
在有序数组中,找出所有满足条件的三元组 (i,j,k),其中 i<j<k,且 nums[j]-nums[i] = nums[k]-nums[j]。这就像在时间轴上寻找三个完美对齐的事件点,形成均匀的时间间隔。
示例:
[2,4,6,8] 包含 2个有效三元组:
-
(0,1,2)→2,4,6(公差2) -
(1,2,3)→4,6,8(公差2)
算法策略
-
固定中间点:
-
以每个元素
j作为中间点,向左右两侧展开侦查。
-
-
双指针魔法:
-
左指针
i从j-1向左移动,右指针k从j+1向右移动,寻找满足等差条件的组合。
-
-
差值平衡术:
-
比较
nums[j]-nums[i]和nums[k]-nums[j],动态调整指针,避免暴力枚举。
-
核心难点:
-
处理重复元素时需小心,避免漏判或重复计数!
#include <stdio.h> // 标准输入输出头文件
/**
* @brief 计算满足等差数列条件的三元组数量
* @param nums 已排序的整数数组指针
* @param numsSize 数组元素个数
* @return 满足条件的三元组数量
*/
int countArithmeticTriplets(int* nums, int numsSize) {
int count = 0; // 初始化计数器为0
// 遍历所有可能的中间点j(从第2个元素到倒数第2个元素)
for (int j = 1; j < numsSize - 1; j++) {
int i = j - 1; // 左指针初始在j的前一个位置
int k = j + 1; // 右指针初始在j的后一个位置
// 双指针向两端扩展寻找满足条件的三元组
while (i >= 0 && k < numsSize) {
int diff = nums[j] - nums[i]; // 计算左差值
int target = nums[j] + diff; // 计算期望的右值
// 检查是否满足等差条件
if (nums[k] == target) {
count++; // 找到一个有效三元组,计数器加1
/* 处理左侧重复元素(虽然本题示例没有重复元素,
但这是为了代码的通用性) */
int left = i - 1;
while (left >= 0 && nums[left] == nums[i]) {
count++; // 每个重复元素都构成新的三元组
left--; // 继续向左检查
}
/* 处理右侧重复元素 */
int right = k + 1;
while (right < numsSize && nums[right] == nums[k]) {
count++; // 每个重复元素都构成新的三元组
right++; // 继续向右检查
}
// 移动双指针继续寻找其他可能的三元组
i--; // 左指针左移
k++; // 右指针右移
}
// 如果当前右值小于期望值,需要增大右值
else if (nums[k] < target) {
k++; // 右指针右移
}
// 如果当前右值大于期望值,需要减小左值
else {
i--; // 左指针左移
}
}
}
return count; // 返回找到的三元组总数
}
/**
* @brief 打印数组内容
* @param arr 数组指针
* @param size 数组大小
*/
void printArray(int* arr, int size) {
printf("["); // 打印左括号
for (int i = 0; i < size; i++) {
printf("%d", arr[i]); // 打印当前元素
if (i != size - 1) printf(", "); // 如果不是最后一个元素,打印逗号
}
printf("]"); // 打印右括号
}
int main() {
// 测试用例
int nums[] = {2, 4, 6, 8};
// 计算数组长度
int numsSize = sizeof(nums) / sizeof(nums[0]);
// 打印初始数组
printf("Input array: ");
printArray(nums, numsSize);
printf("\n");
// 计算并输出结果
int result = countArithmeticTriplets(nums, numsSize);
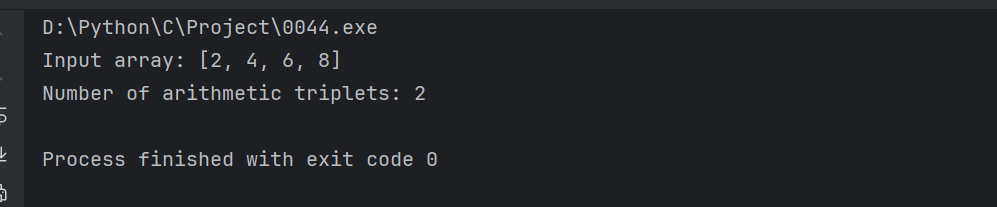
printf("Number of arithmetic triplets: %d\n", result);
return 0; // 程序正常退出
}输出结果:
三、终极对决:算法对比图
| 对比维度 | 质数间隔最大和 | 双指针等差子数组 |
|---|---|---|
| 核心思想 | 排序+质数筛法+区间验证 | 固定中间点+双指针差值平衡 |
| 时间复杂度 | O(n log n)(排序主导) | O(n²)(双指针扫描) |
| 空间复杂度 | O(n)(存储质数索引) | O(1)(原地操作) |
| 适用场景 | 质数相关问题的极值查找 | 有序数组的等差模式匹配 |
| 杀手锏 | 质数快速判断+区间全非质数验证 | 双指针高效跳转+差值动态平衡 |
四、总结:数学与算法的交响曲
-
质数间隔问题像一场战略布局,需要先排序整理战场,再用质数筛法精准定位目标,最后用区间验证确保路径安全。
-
等差子数组问题则像一场动态博弈,通过固定中间点稳住阵脚,再用双指针灵活调整,捕捉差值平衡的瞬间。
二者的共同灵魂在于:利用数学规律减少计算量,通过策略性扫描避免暴力枚举。无论是质数的平方根优化,还是双指针的差值平衡,都彰显了算法设计中“四两拨千斤”的智慧。
结语
今天的算法江湖之旅是否让你意犹未尽?无论是化身质数猎人还是等差数列侦探,算法世界的奇妙冒险永无止境。
互动话题:
-
如果你设计一个算法游戏,会加入怎样的数学挑战?
-
在现实中,你觉得这两个算法能解决哪些有趣的问题?
欢迎在评论区分享你的脑洞!下次我们将解锁更多算法副本,敬请期待!
江湖路远,算法为伴,我们下期再见! 🚀

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










