【无标题】水资源计划

摘  要

淡水资源是世界上许多地方持续发展的限制因素。为了满足中国2035年的用水需求，并确定最优的淡水分配策略。我们通过建立数学模型，为2022年确定一个有效、可行、低成本的用水计划,以满足中国2035年的用水需求，并确定最优的淡水分配策略。该数学模型包括存储、运输、淡化和节水等环节。根据中国各地区历年的水资源总量并求出其均值，参考各地区历年用水总量来预测2035年的用水总量，将两者相减得出差值，我们主要考虑经济因素对两种方案进行分析研究，最终得出结论由水资源丰富地区铺设管道向缺水地区提供水为最优方案。并以各省的省会作为核心城市，说明全省的需水和调水情况，并以省会城市或直辖市为顶点构成一个赋权图，即把问题转换为求水资源丰富地区到缺水地区的最短路问题，并用图论的知识来解决问题。在此基础上考虑到方案会改变就业，生产力，水资源利用等因素，从而对经济，物理，环境产生不同程度的影响，并用层次分析加以研究，最终以报告的方式向政府反映。

关键词：持续发展；最优选择；最小生成树；回归分析

 

 

1 问题重述

淡水资源是世界上许多地方持续发展的限制因素。通过建立数学模型，为2022年确定一个有效、可行、低成本的用水计划,以满足中国2035年的用水需求，并确定最优的淡水分配策略

数学模型必须包括存储、运输、淡化和节水等环节。如果可能，用你的模型来讨论你的策略对经济、自然和环境的影响。提供一个非技术性的意见书给政府领导概述你的方法,包括方法的可行性和成本，以及它为什么是“最好的用水策略选择”

2 模型假设

（1）用水资源总量的影响来代替包括降水量等来水量的影响

（2）将人口数的影响并入到第三产业及生活等其他水的影响当中

（3）假设通过后的影响因素相互独立

（4）假设数据来源可靠准确

（5）从2022年到2035年各外部因素对水资源总量无影响，例如：雪灾、地震、洪水、战争等对环境的影响

（6）各地区海水淡化单位费用相同

（7）不同地区淡水转移的单位费相同

（8）人们的消费水平及劳动力费用不会随意外事故发生明显改变。

3 模型建立

通过在网上查阅数据，我们选取了2017-2021年全国水资源总量及用水量、水资源在生活中的应用等数据，对于这些数据，我们进行了简单的作图分析

收集了近四年来各省的对水资源的需求量的数据，对于2035年各省的水资源的需求量做出估计

4 模型求解

x=[2017 2018 2019 2020 2021]';

y1=[28761.2 27462.5 29041.0 31605.2 29638.2];

y2=[6043.4 6015.5 6021.2 5812.9 5920.2];

plot(x,y1,'-*',x,y2,'-r*');

legend('总量','用水量');

title('2017-2021全国水资源总量及用水量');

figure

近四年的水资源总量变化并不是很大，每年的用水量的十分接近

y3=[1277.0 1261.6 1217.6 1030.4 1049.6];%工业

y4=[3766.4 3693.1 3682.3 3612.4 3644.3];%农业

y5=[838.1 859.9 871.7 863.1 909.4];%生活

y6=[161.9 200.9 249.6 307.0 316.9];%生态

plot(x,y3,'-*',x,y4,'-r*',x,y5,'-g*',x,y6,'-m*');

legend('工业','农业','生活','生态');

title('水资源在生活中的应用');

figure;

 

从图中不难得知，近四年来，农业和工业用水的用量稍有减少，生活用水和生态用水的用量略有上升。用水量最多的是农业用水，用水量最少的是生态用水

通过作图发现，农业工业用水，生活用水和生态用水有的一定的变化，从数据变化的角度加以分析，因此对这些风险因子的选择是合理的

x1=categorical({'beijing','tianjin','hebei','shanxi','neimenggu','liaoning','jilin','heilongjiang','shanghai','jiangsu','zhejiang','anhui','fujian','jiangxi','shandong','henan','hubei','hunan','guangdong','guangxi','hainan','chongqing','sichuan','guizhou','yunnan','xizang','shnxi','gansu','qinghai','ningxia','xinjiang'});

x1=reordercats(x1,{'beijing','tianjin','hebei','shanxi','neimenggu','liaoning','jilin','heilongjiang','shanghai','jiangsu','zhejiang','anhui','fujian','jiangxi','shandong','henan','hubei','hunan','guangdong','guangxi','hainan','chongqing','sichuan','guizhou','yunnan','xizang','shnxi','gansu','qinghai','ningxia','xinjiang'});

y7=[35.4 18.36 187.76 134.5 533.22 317.3 485.42 1176.3 46.7 409.44 1090.86 864.86 943.4 1592.22 332.94 408.86 1132.6 1852.62 1719.42 1996.02 331.9 639.22 2866.08 1113.44 1871.58 4582.24 517.58 317.02 904.2 11.68 871.5];

bar(x1,y7);

title('均值条状图');

从图中可以得知，近四年水资源总量均值较高的是四川、云南、西藏等地，上海、天津、北京等地的水资源总量较少

下面统计各地区的用水量，利用这些数据建立预测模型，拟合出各省相应的线性模型

x=[2017 2018 2019 2020 2021]';

X=[ones(5,1) x];

beijing=[39.5 39.3 41.7 40.6 40.8]';

[b1,bint1,r,rint,stats1]=regress(beijing,X);

b1;bint1;stats1;

z1=b1(1)+b1(2)*x;

w1=b1(1)+b1(2)*2025;%估计2035年的用水

plot(x,beijing,'k+',x,z1,'r')

title('北京');

figure

x=[2017 2018 2019 2020 ]';

X=[ones(4,1) x];

tianjin=[27.5,28.4,28.4,27.8]';

[b2,bint2,r,rint,stats1]=regress(tianjin,X);

b2;bint2;stats1;

z2=b2(1)+b2(2)*x;

w2=b2(1)+b2(2)*2035%估计2035年的用水

plot(x,tianjin,'k+',x,z2,'r')

title('天津');

天津2035年人均用水量预测值

x=[2017 2018 2019 2020 ]';

X=[ones(4,1) x];

hunan=[329.6,337.0,333.0,305.0]';

[b1,bint1,r,rint,stats1]=regress(hunan,X);

b1;bint1;stats1;

z1=b1(1)+b1(2)*x;

w1=b1(1)+b1(2)*2035%估计2035年的用水

plot(x,hunan,'k+',x,z1,'r')

title('湖南');

figure

湖南2035年人均用水量预测值

x=[2017 2018 2019 2020 ]';

X=[ones(4,1) x];

jingsu=[591.3,592.0,619.1,572.0]';

[b4,bint4,r,rint,stats1]=regress(jingsu,X);

b4;bint4;stats1;

z4=b4(1)+b4(2)*x;

w4=b4(1)+b4(2)*2035%估计2035年的用水

plot(x,jingsu,'k+',x,z4,'r')

title('江苏');

figure

江苏2035年人均用水量预测值

x=[2017 2018 2019 2020 ]';

X=[ones(4,1) x];

gansu=[116.1,112.3,110.0,109.9]';

[b5,bint5,r,rint,stats1]=regress(gansu,X);

b5;bint5;stats1;

z5=b5(1)+b5(2)*x;

w5=b5(1)+b5(2)*2035%估计2035年的用水

plot(x,gansu,'k+',x,z5,'r')

title('甘肃');

figure

甘肃2035年人均用水量预测值

x=[2017 2018 2019 2020 ]';

X=[ones(4,1) x];

guangdong=[433.5,420.9,412.3,405.1]';

[b3,bint3,r,rint,stats1]=regress(guangdong,X);

b3;bint3;stats1;

z3=b3(1)+b3(2)*x;

w3=b3(1)+b3(2)*2035%估计2035年的用水

plot(x,guangdong,'k+',x,z3,'r')

title('广东');

figure

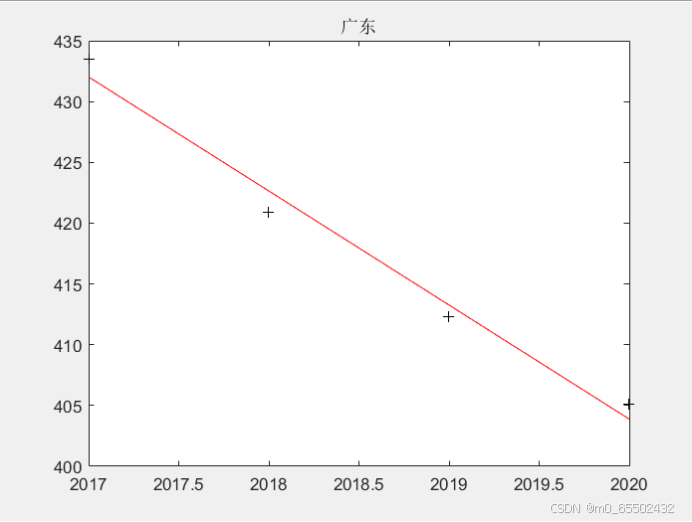
广东2035年人均用水量预测值

其他省市就不再这里一一例举了根据以上信息 ，以水资源总量和用水量为标准，可将中国分为三类地区，缺水区（如北京、天津）、够用区（如辽宁）、丰富区（如云南、湖南、青海）

由最小生成树的思想Prim思路，得出测序结果，并进行分析和讨论

最短路线Y =113+263+175+550+770+270+467+309+57Î+899+638=5025km

综合到南水北调的工程的造价问题，由劳动力的人均费用，以及管道铺设所用的费用等，我们可以平均成工程单位造价问题，然后考虑到单位造价随时间的变化，继续预测出2035年的工程造价。

况

由图表得南水北调的单位造价d为1.7587亿元/km，由此我们估计出2035年输水工程的单位造价d=1.7587亿元/km

即输水工程的总造价为

S=Y*d，即造价为：S=50 2 5 *1.75 8 7=883 7. 5亿元海水淡化：分为两部分，造价=海水的淡化+淡化水的输送

但由初步模型得出的结果，在预测2035年的水资源的差值中，其次所有缺水城市的差值求和，算出总的缺水量 m ，然后从官网上得出得出海水淡化的单位造价d2．再考虑淡化后的水的输送问题。

在靠海的匮水地区，用到海水淡化的方法也是可行的方法，但是在考虑当中要输水的城市不仅只有靠海的城市，像银川等地。所以从34/4134/41紧靠海的匮水城市着手，我们先找出两个靠海城市，上海、天津。然后找出以这两个城市为起点的两条运水路

以下即为淡化后的海水的输运路线。

上海                   南京（270 km )

天津                   北京（113k m )

                          银川（727k m )

石家庄(263km)

因为选取点为靠海城市，即不考虑海到靠海城市的线路。首先，总缺水量由初步模型可得到 m =12.98+11.97+10.69十45.14+134.3+924.84十79.59=1219.5亿吨然后从官方信息网上得出 d ,=5.446亿元／亿吨 s （淡化费）=1219.55.446-6641.4亿元 S ,=5025x1.7587=8837.5

S =5025x1.7587=8837.5分析：虽然 s ,> S （淡化费），但淡化不止存在2025年一年，所以考虑到时间，还是用各城市之间的管道输水经济。所以，最终我们得到适合中国在2035年的最佳水战略为管道输送。

5 模型检验

计算程序为：

 A -[1,1/2,4;2,1,7;1/4,1/7,1]

[ x , y ]= e ig ( A )

 eigen V alue = diag ( y ); 

lamd a = e i gen va lue (1)

У_ lamd a = x (:,1)

计算结果为

lamda =3.0020

Y_lamda =-0.4599

-0.8798

-0.1202

 Aa =3.0020我们求出对应的归一化向量为：W(1)=(0.32 0.60 0.08)T并求出 Cl=(λ-n)/(n-1)=0.001

n=3时，RI=0.58

一致性比率 CR =0.00100.58-0.0017<0.1，通过一致性检验 R 37/4137/41

6 模型评价与建议

我们最初的模型是“线性回归”模型。利用我们的模型可以预测出未来数年的各地区的用水情况。并可以根据预测合理安排水资源。

在接下来的“最小生成树”模型中，我们列举出各城市之间的距离，用Prim模型，得出最短输水方案。我们的模型简单、易懂、也符合实际情况。模型对以后解决此类求最短路问题及其他类似问题提供了有效地方法。根据预测的2035年我国各地区水资源总量与该地区用水总量的差值，把我国分为三个区域，差值＜0为缺水地区，差值在0-1000之间为自给地区，差值＞0为富水地区。

方法：采用由富水地区向缺水地区调水的方法解决缺水地区的用水问题。加强废水的净化来提高水资源的利用率。提高水费来控制用水总量。

参考文献

[1]叶其孝.2013年美国大学生数学建模和跨学科建模竞赛试题[J].数学建模及其应用,2013,2(02):50-52.

[2]付小雪,陈宜金,夏亮亮.北京市水资源利用建模分析研究[J].数学的实践与认识,2014,44(24):191-196.